2. Диэлектрики

1. Вектор поляризованности. 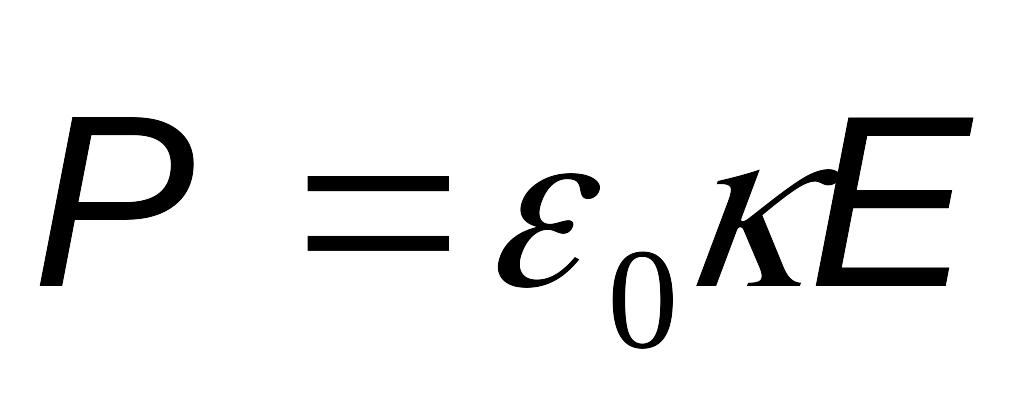, 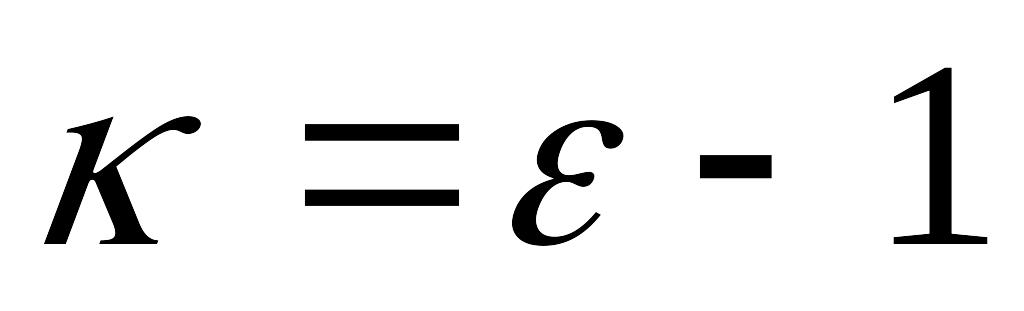Пример: Найти модуль вектора поляризации парафина (ε=2) в электрическом поле напряженностью 13В/м (в 10^-10 Кл/м²)

2. Вектор индукции электрического поля (вектор электрического смещения) 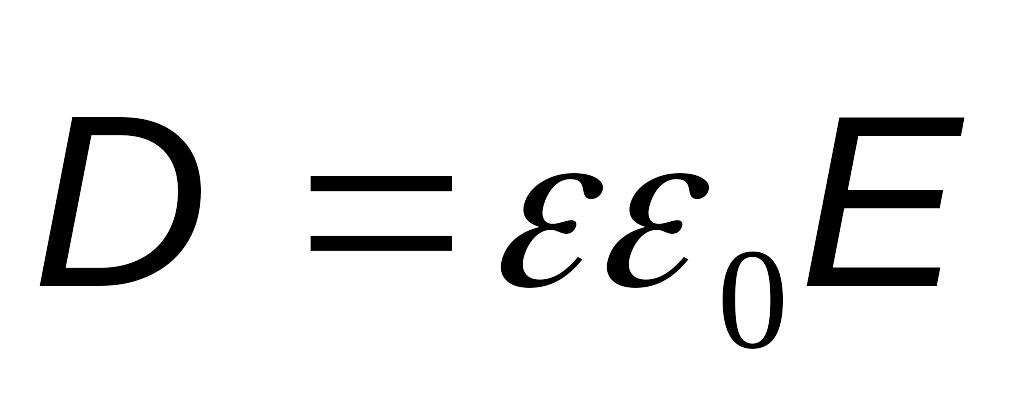Пример: В плоском конденсаторе поверхностная плотность сторонних (свободных) зарядов равна 1.5 нКл/м², а поверхностная плотность связанных зарядов равна 3.0 нКл/м² . Найти модуль вектора электрического смещения (в нКл/м²). Напряженность электрического поля в эбоните (ε=3) Е=0,8 кВ/м. Найти электрическое смещение равно

3. Сегнетоэлектрики. Петля гистерезиса. Коэрцитивная сила. Остаточная поляризованность Пример: В каких веществах наблюдается явление гистерезиса, то есть запаздывания изменения вектора поляризации от изменения напряженности внешнего электрического поля.

4. Плотность энергии электрического поля 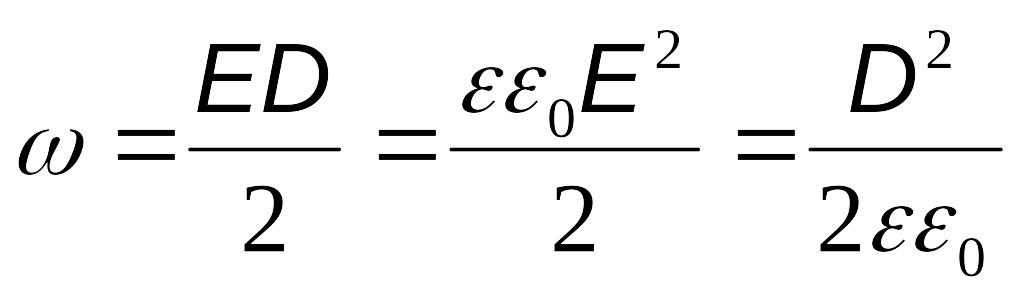Пример: В слюдяном (ε=7) конденсаторе электрическое смещение равно D=2Кл/м². Найти плотность энергии электрического поля в конденсаторе (в ГДж/м³).

5. Теорема Гаусса для диэлектриков Ф_D=Σq_i; 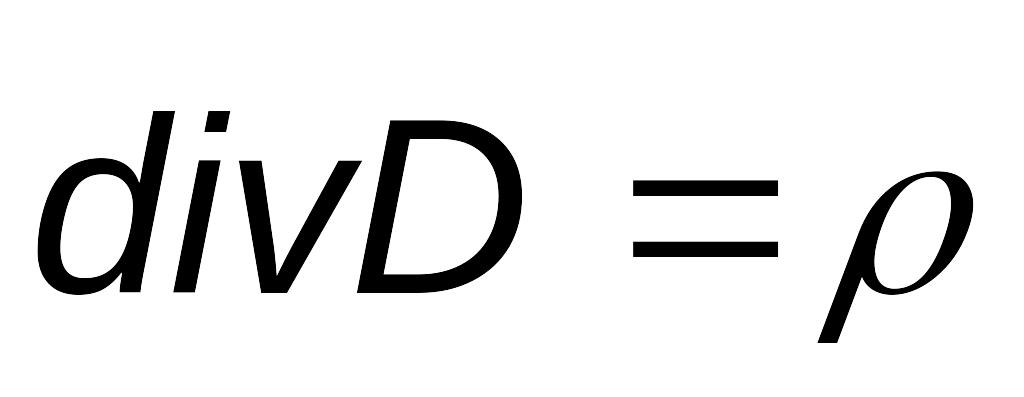Заряд 10 нКл равномерно распределен внутри эбонитового шара радиусом R= 5 м. Найти дивергенцию вектора электрического смещения в центре шара (в мкКл/м³).

3. Проводники. Конденсаторы

1. Напряженность поля вблизи поверхности заряженного проводника Пример: Найти напряженность поля вблизи поверхности проводника, заряженного с поверхностной плотностью заряда σ= 0.5 нКл/м².

2. Электроемкость уединенного проводника. С = Q/φ

3. Конденсатор. Электроемкость конденсатора. C = Q/U

4. Разрядка и зарядка конденсатора через сопротивление I = I₀exp(-t/(RC)) Разрядка: U = U₀exp(-t/(RC)) Зарядка: U=E(1- exp(-t/(RC)) Пример: За сколько времени в конденсаторе емкостью С= 2,5 мкФ при разрядке через сопротивление R=1,2 МОм заряд уменьшится в 2,72 (в с).

5. Плоский конденсатор

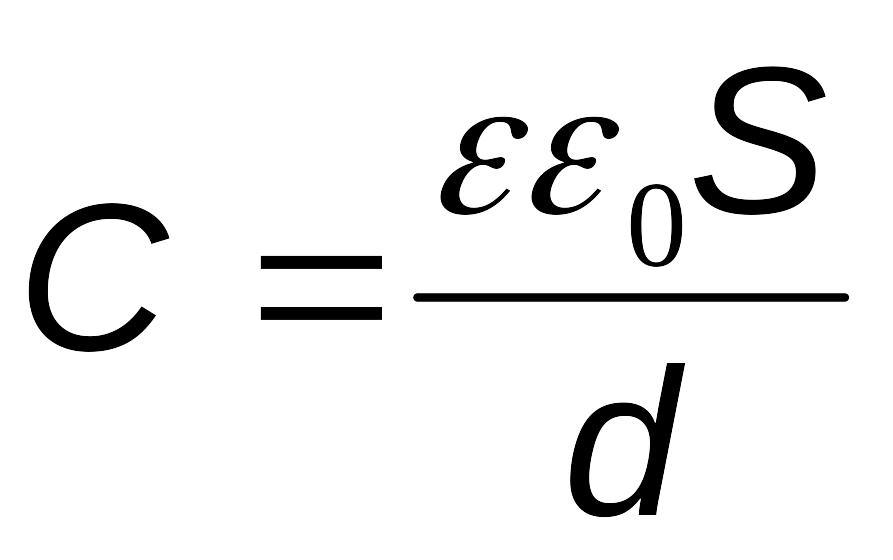
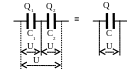
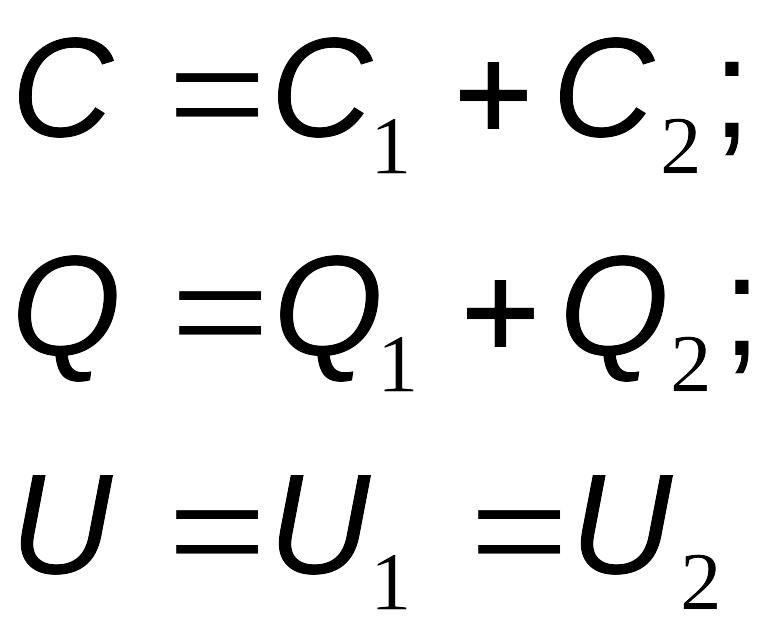6. Соединения конденсаторов Последовательное: Параллельное: 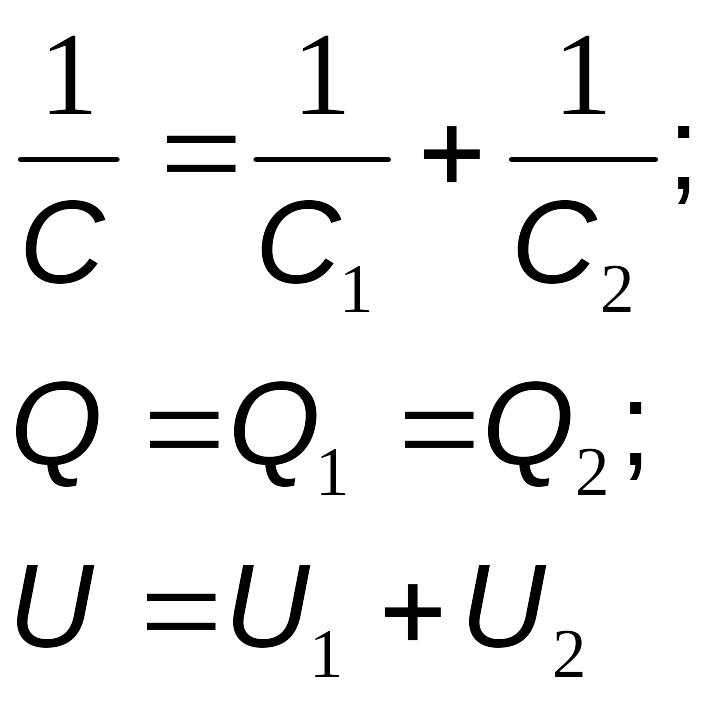Пример:

Найти емкость батареи конденсаторов

Найти напряжение на конденсаторе 4мкФ

7. Сопротивление цилиндрического проводника

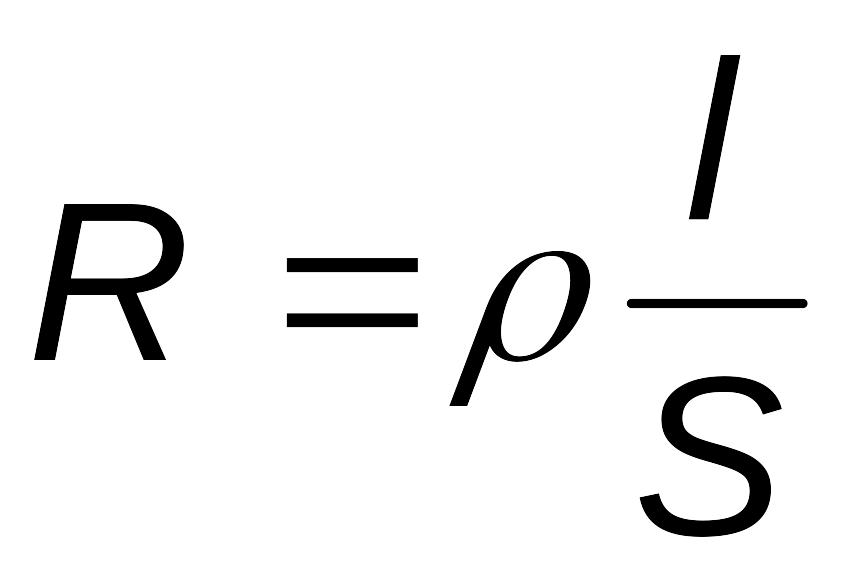
8. Закон Ома в дифференциальной форме 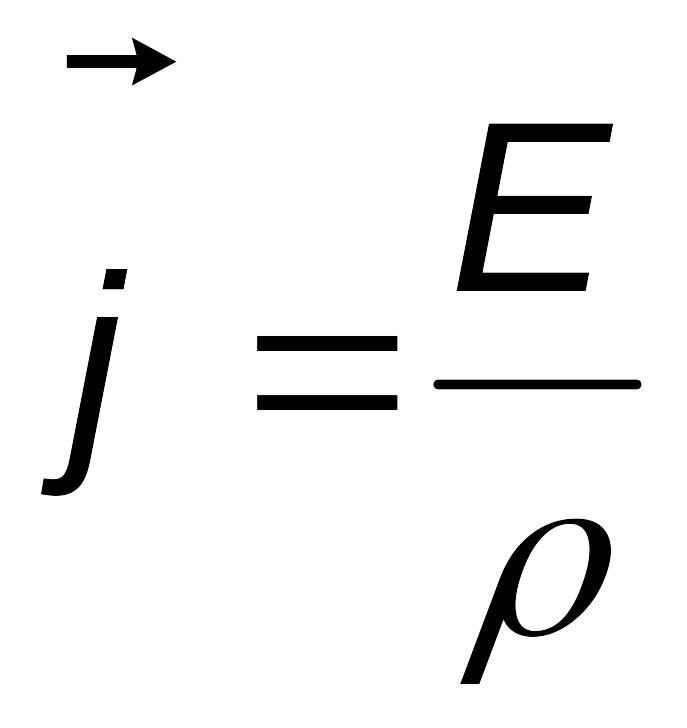Пример: По проводнику течет ток плотностью j=1 х10⁶ А/м², напряженность электрического поля в проводнике равна E=10 мВ/м. Найти удельное сопротивление проводника равно (в нОм·м)

9. С оединение сопротивлений Последовательное 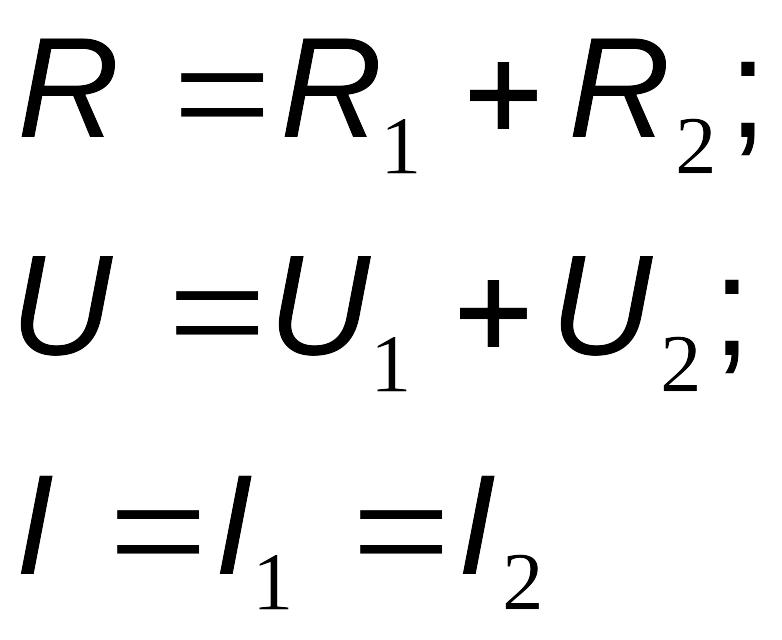Параллельное

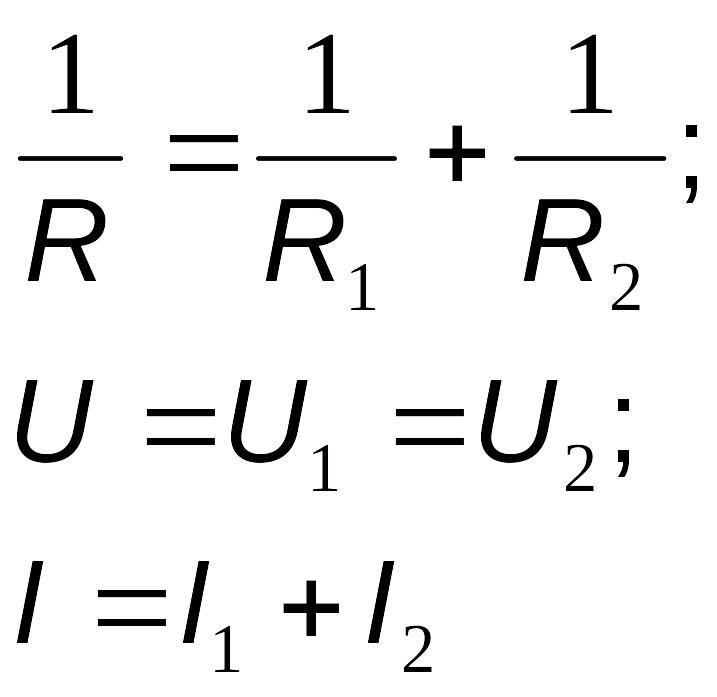
4. Энергия заряженных систем

1. Э 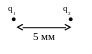нергия взаимодействия точечных зарядов Пример: Найти энергию взаимодействия зарядов q₁= -5 мкКл и q₂ = +3мкКл (см рис.) (в Дж). Пример Потенциал поля, созданный двумя зарядами в точке нахождения третьего равен 1 В. Найти энергию системы (см.рис.) (в нДж).

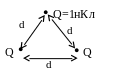
2. Энергия заряженного конденсатора 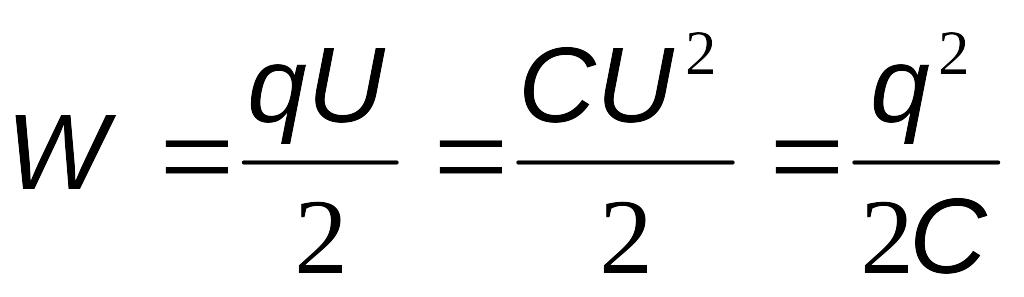Пример: Расстояние между обкладками плоского воздушного конденсатора, подключенного к источнику тока, увеличили в 2 раза. Как изменилась энергия конденсатора.

3. Плотность энергии поля