2 Анализ структурной схемы автоматического управления

2.1 Исходные данные

Коэффициент передачи K1 0,5

Коэффициент передачи K2 0,25

Коэффициент передачи K3 0,2

Коэффициент передачи K4 2

Установившаяся ошибка ξ,% 0,5

Перерегулирование δ,% 20

Время регулирования t₀, С 3

Оператор дифференцирования S С^-1

2.2 Преобразование структурной схемы системы автоматического управления (сау)

Исходная структура состоит из трёх сумматоров, трёх интегрирующих звеньев и трёх без инерционных звеньев, приложение А, рисунок 1.

Сумматоры имеют по два входных порта и по одному выходному порту.

Интегрирующие звенья с передаточными функциями соответственно:

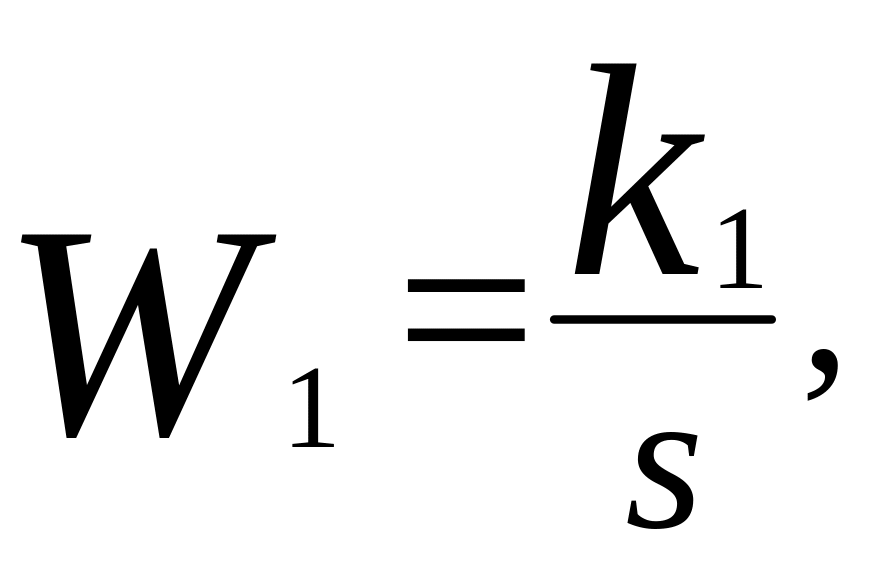
Безинерционные звенья с передаточными функциями соответственно:

W₄=K2, W₅=K3, W₆=K4;

Проведем преобразование структуры (приложение А, рисунок 1) используя из­вестные правила, которые изложены в Л.[4] В задании на проектирование динамические звенья включены встречно - параллельно и последовательно.

Для встречно параллельного включения формула преобразования имеет вид:

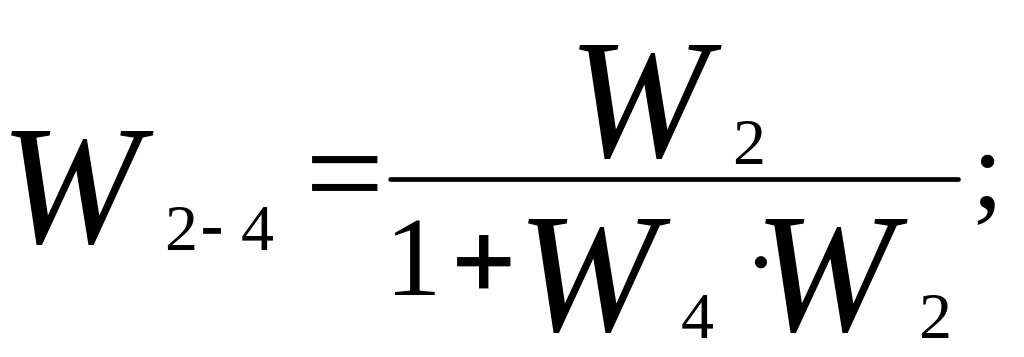(2.1)

где W₂ - передаточная функция в прямой цепи управления;

W₄ - передаточная функция в обратной цепи управления.

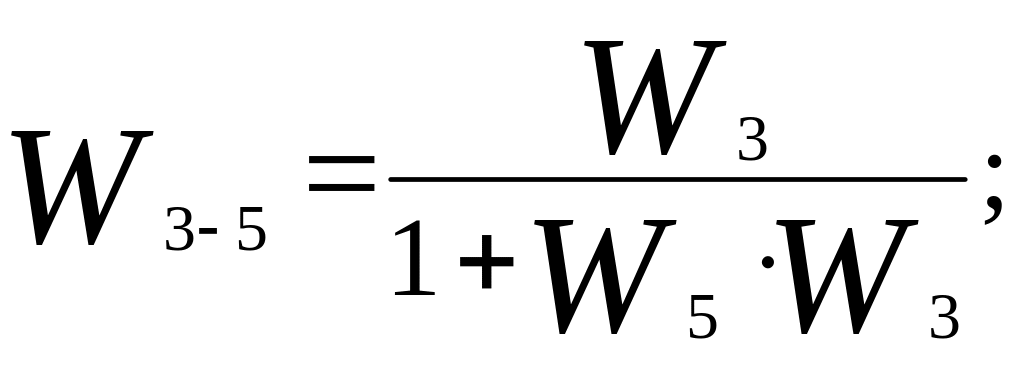(2.2)

где W₃ - передаточная функция в прямой цепи управления,

W₅ - передаточная функция в обратной цепи управления.

Определим передаточную функцию прямой цепи управления одноконтурной структурной схемы, используя правило преобразования для последовательного включе­ния динамических звеньев:

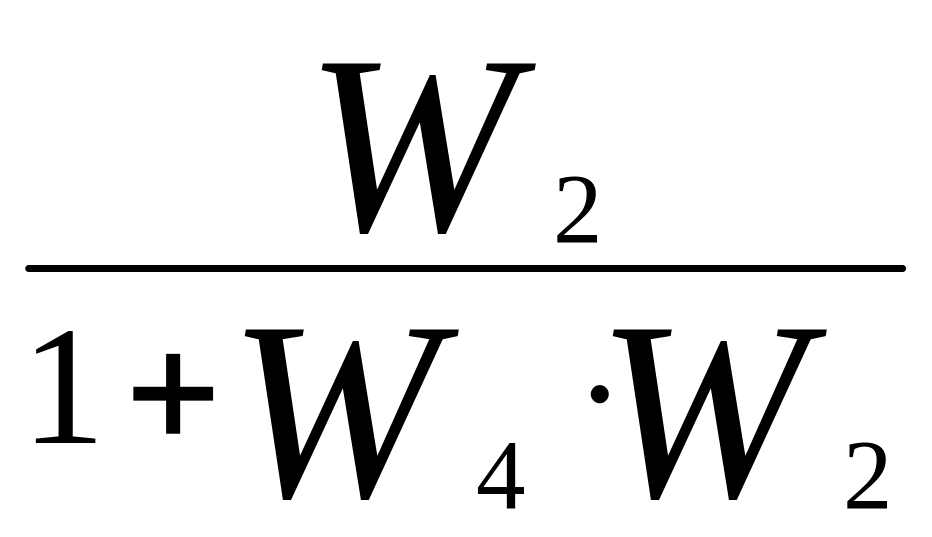
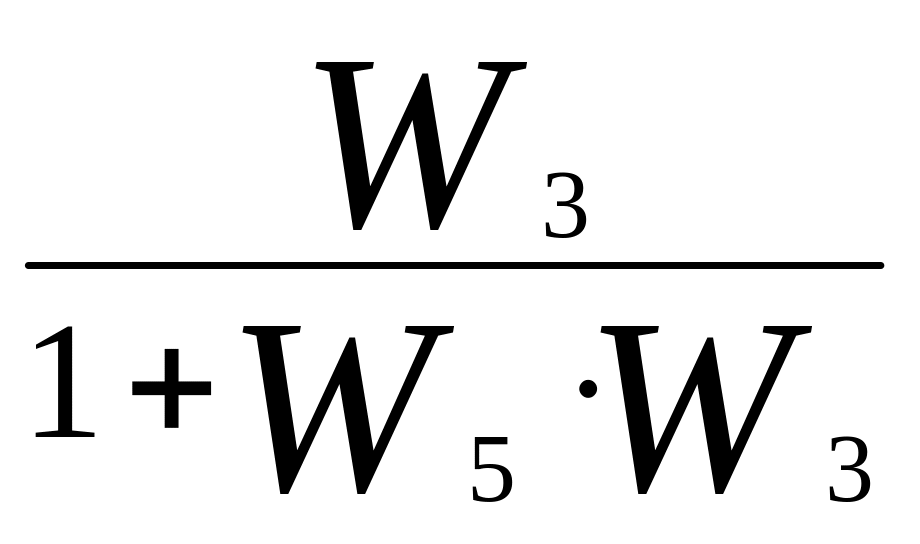
(2.3)

где - передаточная функция первого динамического звена;

Используя выражения 2.1 и 2.3, определим структуру одноконтурной системы управления соответствующую приложению А, рисунок 2.

Передаточная функция в обратной цепи управления для этой структурной схемы имеет вид:

W₆ = К₄

Определим статическую точность исходной САУ. Для этого проанализируем выражение 2.3. Как видно из этого выражения в прямой цепи управления есть интегри­рующие звено 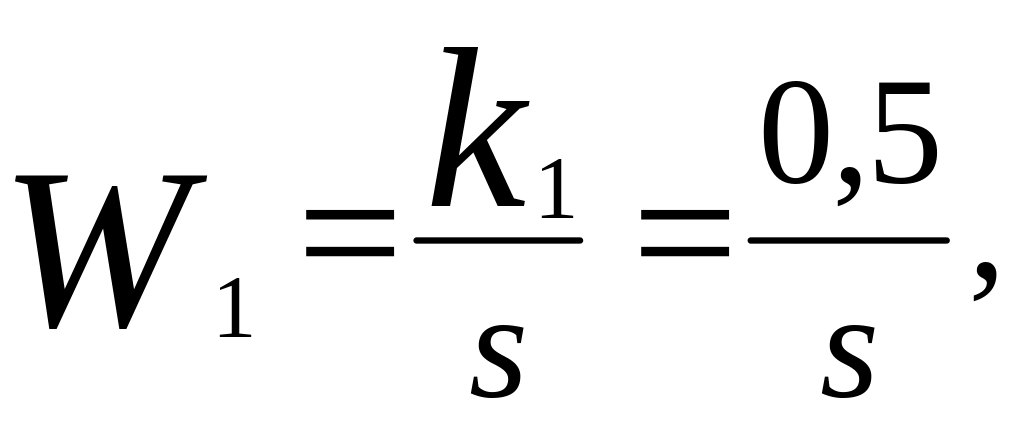а значит система астатическая - она не имеет статиче­ской ошибки в установившемся режиме.

2.3 Проверка на устойчивость заданной сау.

Приведем структуру, которая соответствует приложению А рисунок 2

к структуре, соответствующей приложению А, рисунок 3 используя следующие выраже­ние:

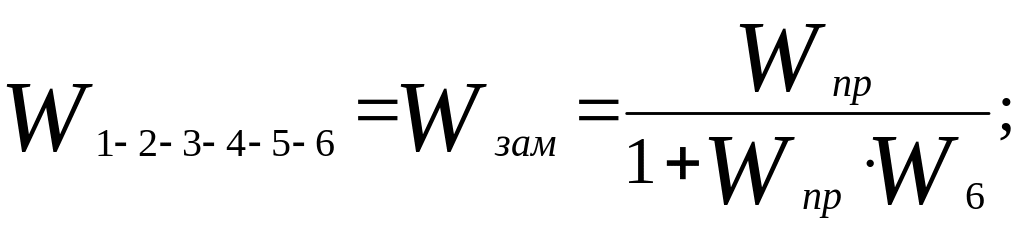
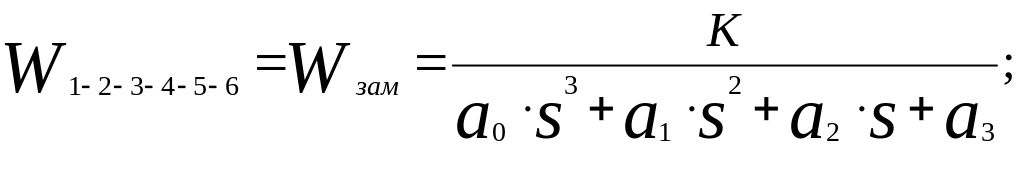(2.4)

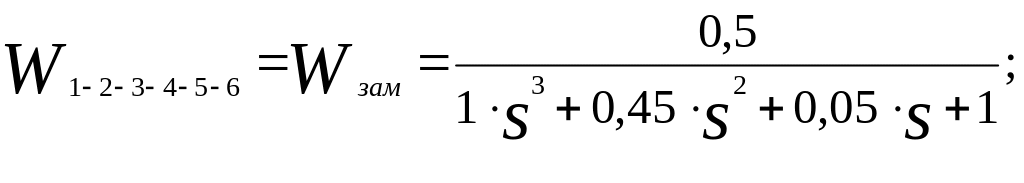
2.4 Определение устойчивости сау по критерю Гурвица

Используя критерий Гурвица и знаменатель выражения 2.4, определим ус­тойчивость САУ. Знаменатель выражения 2.4 представляет собой характеристическое уравнение замкнутой системы. Предварительно введем следующие обозначения:

а₀=1, а₁=0,45, а₂=0,05 а₃=1.

Как видно из выражения 2.4, автоматическая система представляет собой устройство третьего порядка. В этом случаи для того, чтобы САУ была устойчивой не­обходимо и достаточно выполнение следующих неравенств:

а₀0, а₁0, а₂0, а₃0, (2.5)

а₁*а₂-а₀*а₃0. (2.6)

Подставим значения коэффициентов в характеристические неравенства 2.5 и 2.6

10, 0,450, 0,050, 10,

0,45*0,05-1*1<0.

система не устойчива т. к. условие 2.6 не выполнено.

2.5 Моделирование исходной сау

Моделирование проводим, во первых с целью проверки правильности преобразо­ваний выполненных в пункте 2.2 и, во вторых, для анализа результатов моделирования динамических характеристик САУ.

В новой версии MatLab 6 приложение Simulink3 имеет динамическую связь с па­кетом Control System Toolbox, позволяющим исследовать динамические характеристики системы. На эту связь указывает меню Tools в строке меню модели. В частности, можно получить следующие характеристики:

• переходную характеристику - реакцию системы на ступенчатое единичное воздей­ствие;

• амплитудо - частотную и фазо - частотную характеристики;

• расположение полюсов и нулей передаточной функции системы.

Исследуемые модели, набранные в рабочем поле модельного окна, соответст­вуют рисунку 1.

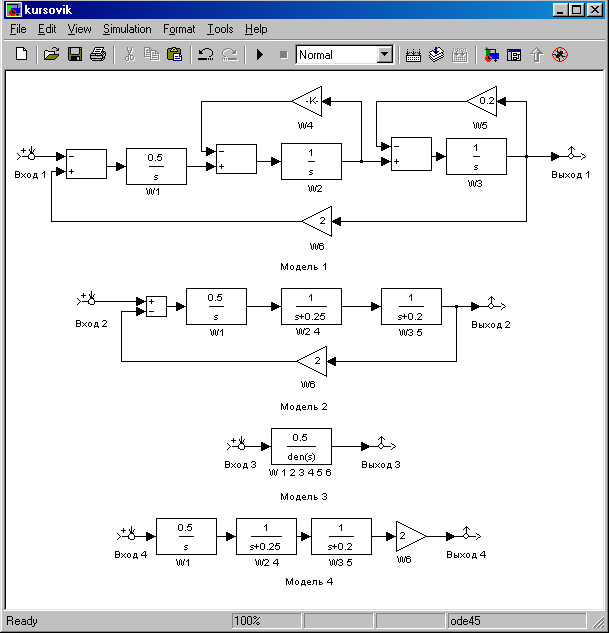
Рисунок1 - Исследуемые модели.

Процесс моделирования проводим в следующей последовательности:

• в модельном окне выбираем пункт меню Tools;

• в открывающемся окне меню Tools выбираем опцию Linear Analysis, при этом появля­ется окно дополнительной библиотеки входных и выходных портов Model Inputs and Outputsи, изображённое на рисунке 2, и пустое окно блока LTI Viewer, соответствующее рисунку 3;

• входные и выходные порты, как обычные библиотечные блоки, «перетаскиваются» в окно модели и присоединяются ко входам и выходам исследуемых моделей;

• проводим динамическое моделирование. Для этого в выпадающем меню Simulink окна LTI Viewer выбираем опцию Get Linearized Model.

• выбираем из меню Plot Types необходимые для исследования типы характеристик.

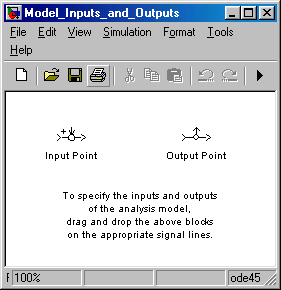
Рисунок2 - Вид окна Model Inputs and Outputs.

В окне LTI Viewer отображаются результаты моделирования.

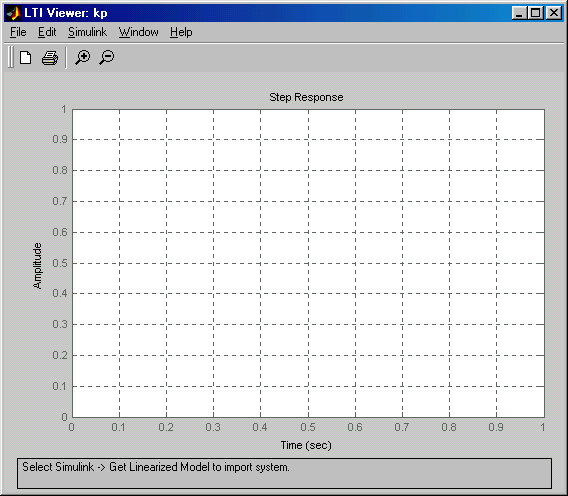
Рисунок3 - Вид окна блока LTI Viewer.

Для модели 1 выводим переходную характеристику и расположение полюсов и нулей передаточной функции системы, которые соответствуют приложению В, рисунок 1, рисунок 2.

C целью проверки правильности преобразования модели 1, выводим переходную характеристику и расположение полюсов и нулей передаточной функции модели 2, кото­рые соответствуют приложению С рисунок 1 рисунок 2.

С целью проверки правильности преобразования модели 2, соответствующей рисунку, 1, выводим переходную характеристику и расположение полюсов и нулей пере­даточной функции модели 3,которые приведены в приложении D рисунок 1, рисунок 2.

Для модели 4 выводим графики амплитудно-частотной и фазо-частотной ха­рактеристик разомкнутой системы, которым соответствует приложение E