20. Типы кристаллических твердых тел: металлы, диэлектрики. Полупроводники с собственной и примесной проводимостью.

Порядок в расположении узлов кристаллической решетки приводит к тому, что в твердых телах существует электрическое поле, которое является периодической функцией координат. Это поле существенно изменяет энергетический спектр электронов в твердом теле по сравнению с их спектром в изолированных атомах. В изолированных атомах электроны находятся на дискретных уровнях энергии (рис 1Б). В кристалле, состоящем из N атомов, из-за взаимодействия атомов одиночные уровни энергии электронов расщепляются в N близко расположенных уровней, которые образуют зону (рис. 1А).

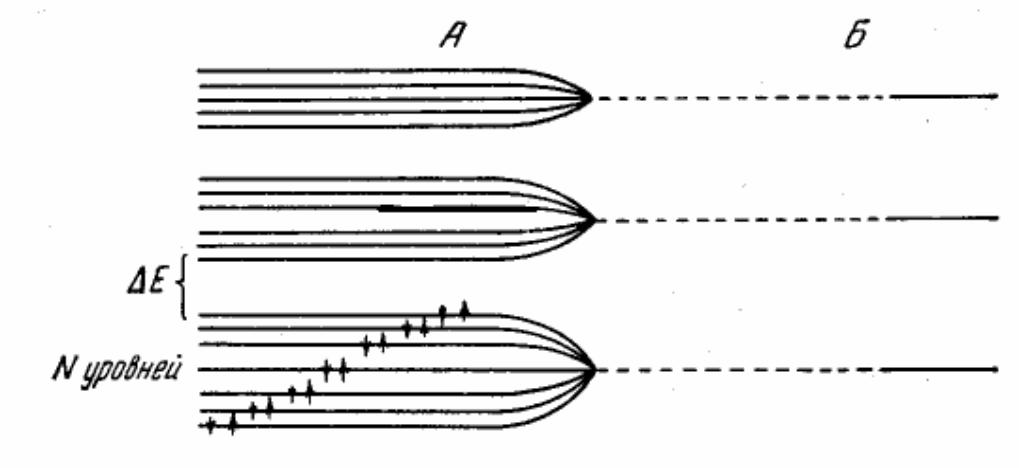
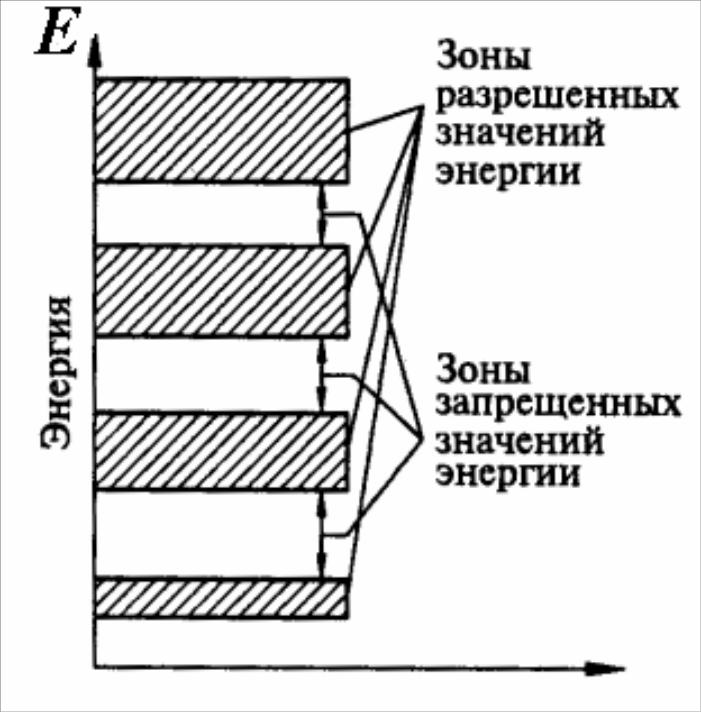
Рис.1 Рис. 2

На каждом уровне энергии в зоне может находиться по два электрона с противоположно ориентированными спинами. Соседние энергетические уровни в зоне отстоят друг от друга примерно на расстоянии 1/N эВ. Разрешенные зоны разделены запрещенными зонами. С увеличением энергии ширина разрешенных зон увеличивается, а запрещенных – уменьшается (рис.2).

Различия в электрических свойствах между металлами, диэлектриками и полупроводниками объясняют, используя представление о зонах.

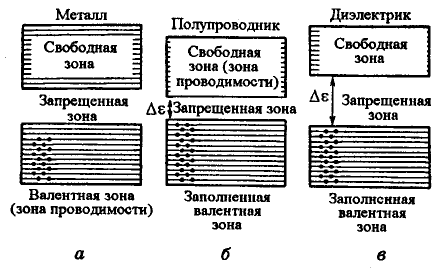Рис. 3

Типичными представителями проводников являются металлы первой группы периодической системы Менделеева, например, натрий. Его электронная конфигурация 1s²2s²2p⁶3s¹. Это одновалентный элемент, он имеет две полностью заполненные оболочки (K-, L-оболочку) и на его внешней оболочке находится только один электрон. В кристалле натрия двум полностью заполненным оболочкам изолированного атома соответствуют полностью заполненные зоны, а внешние электроны атомов натрия заполняют половину уровней разрешенной зоны. Такая зона называется зоной проводимости, так как находящиеся в ней электроны участвуют в создании тока. Таким образом, если разрешенная зона не полностью занята электронами, то кристалл всегда будет проводником.

Для элементов второй группы периодической системы Менделеева соседние разрешенные зоны могут пересекаться. При этом образуется широкая зона, заполненная электронами частично, такая зона также является зоной проводимости и такие кристаллы – проводниками.

В диэлектриках разрешенные зоны не перекрываются, запрещенные зоны широкие, поэтому электроны из заполненных зон не могут перейти в вышележащие свободные разрешенные зоны. Зона, полностью заполненная электронами, называется валентной, а находящаяся над ней пустая разрешенная зона – зоной проводимости. Примером диэлектрика является поваренная соль.

В полупроводниках при Т0 электроны заполняют зоны так же, как в диэлектриках. Поэтому полупроводники при Т0 электрический ток не проводят. Но ширина запрещенных зон у полупроводников меньше, чем у диэлектриков, поэтому при повышении температуры часть электронов из валентной зоны переходит в зону проводимости. На месте ушедших электронов в валентной зоне образуются дырки. Дырка ведет себя как положительный заряд, равный по величине заряду электрона. Проводимость полупроводника, обусловленная наличием дырок в валентной зоне и электронов в зоне проводимости называется собственной проводимостью.

На практике особенно большое значение имеют полупроводники, проводимость которых обусловлена примесями.

Рассмотрим два случая.

1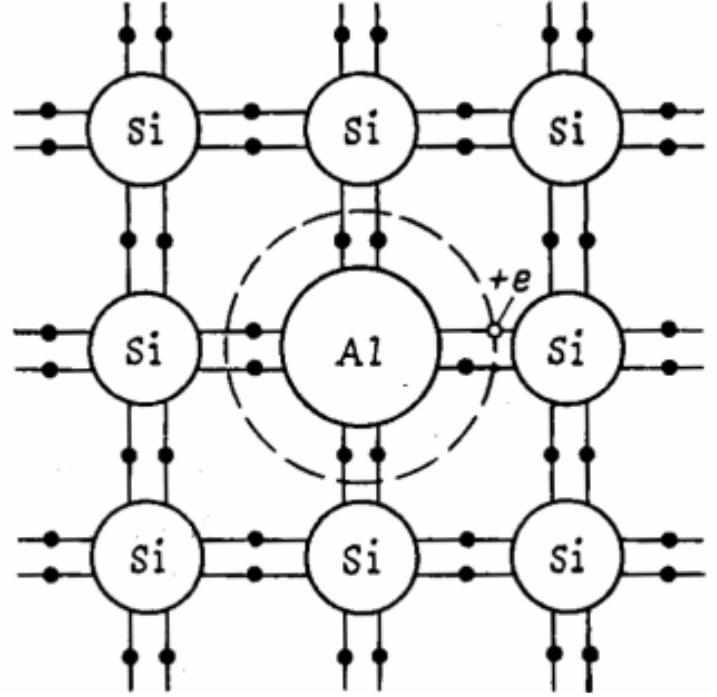 ) Пусть в кристалл кремния введена примесь мышьяка. Кремний четырехва лентный элемент, а мышьяк – пятивалентный. В решетке кремния 4 валентных электрона кремния образуют ковалентную связь с 4 валентными электронами мышьяка. Пятый электрон мышьяка, не принимающий участия в ковалентной связи, слабо связан с мышьяком. При низких температурах он находится около мышьяка, а при повышении температуры может свободно перемещаться по кристаллу. Доминирующую роль в проводимости будут играть электроны. Такие полупроводники называют полупроводниками n-типа, а примесь, дающую электроны – донорной.

2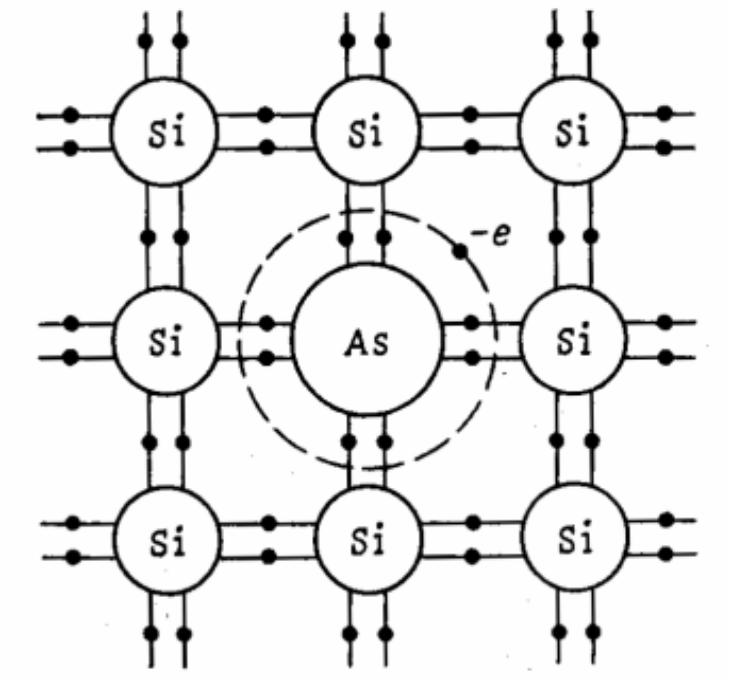 ) Пусть в кристалл кремния введена примесь алюминия. Алюминий – трехвалентный элемент. Три электрона алюминия образуют ковалентные связи с тремя электронами соседних атомов кремния, а одна связь соседнего кремния будет не завершена. В незаполненную связь около алюминия будет захвачен электрон от соседнего кремния. При этом будут образовываться положительные дырки, которые будут перемещаться по кристаллу. Примеси, захватывающие электроны, называются акцепторными, полупроводник с акцепторной примесью называется полупроводником p-типа.

Полупроводник, имеющий примеси, называется примесным. Проводимость, обусловленная примесями – примесной проводимостью. Наличие примесей в кристалле вызывает появление дополнительных уровней энергии, которые располагаются в запрещенной зоне. При этом уровень донорной примеси располагается ближе к зоне проводимости, а уровень акцепторной примеси располагается ближе к валентной зоне.

Рис. 4 Рис. 5

На рис.4 и 5 черные кружки – электроны, белые – дырки. На рис. 4 электроны с донорного уровня поступают в зону проводимости. На их месте остаются дырки. Это механизм примесной проводимости. Кроме того, электроны могут перейти из валентной зоны в зону проводимости. Это механизм собственной проводимости. На рис. 5 акцепторный уровень захватывает электроны из валентной зоны. На месте ушедших электронов в валентной зоне образуются дырки. Это механизм примесной проводимости. Как и в случае рис. 4, на рис.5 изображен еще механизм собственной проводимости.