Задача 5

Доказать, что если точка с барицентрическими координатами и принадлежат некоторой прямой, то той же прямой принадлежит точка с координатами .

Решение:

Пусть точки а (х1,х2,х3,х4) и в (y1y2y3y4) заданы барицентрическими координатами. Тогда (о-полюс) имеют те же координаты. Отсюда

.

Условие является условием принадлежности точки М(z₁,z₂,z₃,z₄) прямой АВ. Приравнивая координаты получим:

При получаем интересующее равенство.

Задача 6

Пусть - площади граней DCD, ACD, ABD и ABC тетраэдра ABCD. Найти координаты центра вписанной сферы.

Решение:

Пусть точка Р- центр сферы с барицентрическими координатами (₁,₂,₃,₄), тогда используя метрический смысл барицентрических координат, получим:

,

причем, d_i =R (радиус сферы). С другой стороны

,

то есть

,

тогда

Точка Р имеет координаты .

Задача 7

Поставим задачу определить расстояние между точками М и Р если известны барицентрические координаты _i точки Р и расстояния точки М от вершин А_i данного тетраэдра.

Решение:

Пусть _i- барицентрические координаты точки Р относительно тетраэдра А₁А₂А₃А₄. Тогда для любого вектора имеет место равенство:

,где . (3.2)

При любом выборе точки О в качестве полюса

.

Поэтому

,

так как ₁+₂+₃+₄=1.

Вычислим скалярный квадрат вектора . Воспользовавшись равенством (3.2), будем иметь:

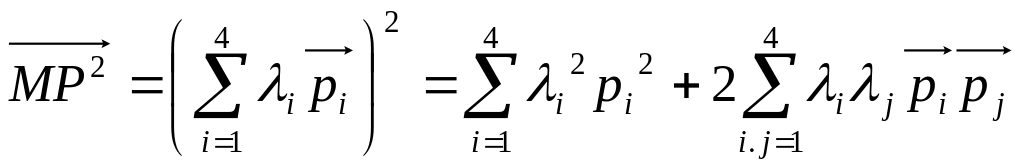, i<j.

Но

,

поэтому

, i<j

После несложных преобразований находим, что

, i<j

и окончательно

, i<j. (3.3)

Задача 8

Используя решение предыдущей задачи определим расстояние между некоторыми замечательными точками тетраэдра.

Решение:

1) Пусть точка М совпадает с центром О описанной около тетраэдра сферы. Если R-радиус сферы , то все . Точку Р поместим в центроид G тетраэдра. Для нее . Согласно (3.3) будем иметь:

, i<j (3.4)

Из (3) следует, что для всякого тетраэдра имеет место неравенство:

, i<j,

причем знак неравенства следует писать тогда и только тогда, когда центроид и центр описанной сферы совпадают.

2. Если точка G- центроид тетраэдра, а точка М совпадает с одной из вершин тетраэдра, например, с вершиной А₄ , то и равенство (3.3) в этом случае принимает вид :

,i<j,

или

.

Учитывая, что где G_i – центроид грани , отсюда получаем формулу для вычисления длины медианы тетраэдра через длины его ребер:

.

Задача 9

Пусть точка Р- точка, не лежащая на сторонах косого четырехугольника А₁А₂А₃А₄, через которую проведены две прямые, пересекающие попарно различные его противоположные стороны, соответственно в точках Р₁₂, Р₃₄ и Р₂₃, Р₄₁ (рис. 3.3), а так же заданы отношения , в которых они делят соответствующие стороны

.

По теореме Менелая для А₁А₂А₃А₄ =1 .

Найти в каком отношении делит точка Р отрезки Р₁₂Р₃₄ и Р₂₃Р₄₁, то есть

.

Рисунок 3.3