Задача 5

Довести, що якщо точка с барицентричними координатами 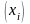та належать деякій прямій, то тій же прямій належить точка з координатами .

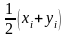Розв язання:

Нехай точки а (х1,х2,х3,х4) и в (y1y2y3y4) задані барицентричними координатами. Тоді (о-полюс) мають ті же координати. Отже

.

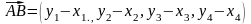Умова 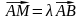є умовою приналежності точки М(z₁,z₂,z₃,z₄) прямій АВ. Прирівнюючи координати отримаємо:

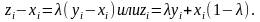
При . Отримуємо рівність, що цікавить Задача 6

Нехай - площини граней DCD, ACD, ABD и ABC тетраєдра ABCD. Знайти координаті центра вписаної сферы.

Розв язання:

Нехай точка Р- центр сфери с барицентричними координатами (₁,₂,₃,₄), тоді використовуя метричний смисл барицентричних координат, маємо:

,

тоді, d_i =R (радиус сфери). С іншої сторони

,

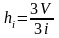тобто

,

тоді

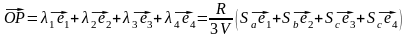
Точка Р має координати .

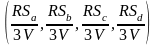Задача 7

Поставимо завдання визначити відстань між точками М і Р якщо відомі барицентричні координати _i точки Р та відстань точки М від вершин А_i даного тетраєдра.

Розв язання:

Нехай _i- барицентричні координати точки Р відносно тетраєдра А₁А₂А₃А₄. Тоді для будь якого вектора має місто рівність:

,где 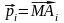. (3.2)

При будь-якому виборі точки О в якості полюса

.

Тому

,

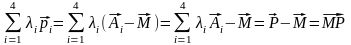так як ₁+₂+₃+₄=1.

_{Обчислимо скалярний квадрат вектора} . Скориставшись рівністю(3.2), матимемо

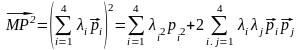, i<j.

але

,

тому

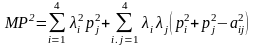, i<j

Після нескладних перетворень знаходимо, що

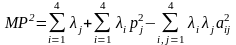, i<j

та остаточно

, i<j. (3.3)

Задача 8

Використовуючи розв язання попередньої задачі визначимо відстань між деякими чудовими точками тетраедра.

Розв язання:

1) Нехай точка М співпадае с центром О описаної навколо тетраєдра сфери. Якщо R-радіус сфери , то всі 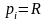. Точку Р розмістемо в центроід G тетраєдра. Для неї 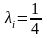. Відповідно (3.3) будем мати:

, i<j (3.4)

З(3) витікає, що для всякого тетраедра має місце нерівність:

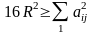, i<j,

причому знак нерівності слід писати тоді і тільки тоді, коли центроїд і центр описаної сфери співпадають.

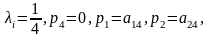
2. Якщо точка G- центроід тетраедра, а точка М співпадае с однією з вершин тетраедра, наприклад, з вершиною А₄ , то 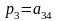рівність (3.3) в цьому випадку приймає вид :

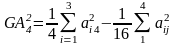,i<j,

або

.

Враховуючи, що где G_i – центроід грані , звідси отримуємо формулу для обчислення довжини медіани тетраедра через довжини його ребер :

.

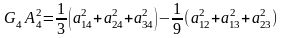Задача 9

Нехай точка Р- точка, що не лежить на сторонах косого чотирикутника А1А2А3А4, через яку проведені дві прямі, що перетинають попарно різні його протилежні сторони, відповідно в точках Р12, Р34 і Р23, Р41(мал. 3.3), а так само задані стосунки, в яких вони ділять відповідні сторони

.

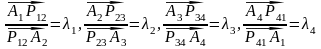По теореме Менелая для А₁А₂А₃А₄ =1 .

Знайти у якому відношенні ділить точка Р відрізку Р12Р34 і Р23Р41, тобто

.

Рисунок 3.3