3.Косий чотирикутник в прикладах і завданнях Задача 1

Дани чотири прямі, жодні три з не яких компланарни, тоді існує косий чотирикутник, сторони якого паралельні цим прямим.

Доведення:

Нехай - векторы, паралельні даным прямим. Так як будь які три прямі з даних не компланарни, то їх направляючі вектори так само не компланарні, таким чином вони утворюють базис. Тоді четвертий направляючий вектор може бути представлений як їх лінійна комбінація, тобто розкладений по векторах базису.

Візьмемо за базисні вектори , тоді

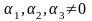
або

.

Легко побачити, що на векторах 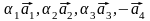можно побудувати косий чотирикутник.

Задача 2

а) Скільки існує попарно не рівних просторових чотирикутників з одним і тим же набором векторів?

б) Доведіть, що об'єм всіх тетраедрів, заданих цими просторовими чотирикутниками, рівні.

Розв язок :

а) Якщо задані сторони просторового чотирикутника у вигляді векторів , то сума всіх цих векторів має бути рівною нулю. Якщо від А відкласти , то В є кінцем,от якого можна відкласти три вектори . Отже існують три варіанти вибору другого вектора. Якщо другий вектор вибраний, то третій можна вибрати двома способами. Тобто варіантів вибору трьох векторів існує 32=6. Останній вектор можна вибрати лише одним способом.

Це означає що існую всього 6 попарно не рівних просторових чотирикутників з одним і тим же набором векторів.

б) Нехай а,b,c і d – дані вектори сторін. Розглянемо паралелепіпед, що задається векторами а,b і с (мал. 3.1); його діагоналлю служить вектор d . Нескладний перебір показує, що все шість різних чотирикутників містяться серед чотирикутників, сторонами якого є ребра цього паралелепіпеда і його діагональ d (фіксувати при переборі зручно вектор d). Об'єм кожного відповідного тетраедра складає 1/6 частина об'єму паралелепіпеда.

Рисунок 3.1

Задача 3

Нехай в просорі задан тетраэдр А₁А₂А₃А₄.

а) Довести, що будь яка точка Х має деякі барицентричні координати відносно його.

б) Довести, що при умові m₁+m₂+m₃+m₄=1 барицентричні координати точки Х визначени однозначно.

Розв язок:

Рисунок 3.2

а) Введемо наступні позначення:

и .

Точка Х є центром мас вершин тетраедра А1А2А3А4 (ріс.3.2) з масами m1,m2,m3,m4 тоді і лише тоді, коли

тобто

, (3.1)

де m=m₁+m₂+m₃+m₄.

Враховуючи , що m=1 в (3.1).

б) Доведемо однозначність барицентричних координат. Будь-який вектор можна представити у вигляді

,

причому числа m1,m2,m3 визначені однозначно. Число m4 знаходиться по формулі:

m₄=1-m₁-m₂-m₃,

_{тобто визначена також однозначно.}

Задача 4 в системі барицентричних координат, пов язаних с тетраэдром а1а2а3а4.

Знайти рівняння:

а) прямой А₁А₂;

б) площини А₁А₂А₃;

в) площини, перетинаючи А₃А₄ параллельно А₁А₂.

Розв язок:

а) Нехай точка О - полюс системи барицентричних координат, точка М( ) – довільна точка (А₁А₂), тоді

(з визначення барицентричних координат).

 , = ,

, ,

або

тобто , , .

Точка с барицентричними координатами 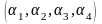лежить на прямій , якщо . Таким чином векторне рівняння (А₁А₂) має вигляд

.

б) Нехай точка М належить (А₁А₂ А₃) , тоді

.

Використаємо геометричний смисл барицентричних координат. Отримуємо

.

Точка М належить площині (А₁А₂А₃ ), якщо . Таким чином векторне рівняння площини має вигляд

.

в) Нехай:

- базис.

Для точки , такой що  , можно записати

.

и утворюють базис площини(А4ХА3), тоді для будь-якої точки цієї площини

, .

Розв яжемо задачу за допомогою барицентричних координат.

Введемо базис . Тоді

.

, ,

 ,

с однієї сторони.

З іншої сторони

.

В силу єдиності розкладання вектора, отримуємо

,

.
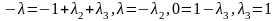