Конспект лекция по метрологии (группа ЗС-2-04) / Задачи № 2

Задача

Найти одномерную и двумерную плотности вероятности случайного процесса

,

гд6е - постоянная величина, a, b – независимые случайные нормально распределенные величины с нулевым средним и дисперсией

Ответ

Случайная величина при любом фиксированном t представляет собой линейную комбинацию нормально распределенных случайных величин и в силу этого является также нормально распределенной. Следовательно, для определения плотности вероятности надо найти среднее значение и функцию корреляции

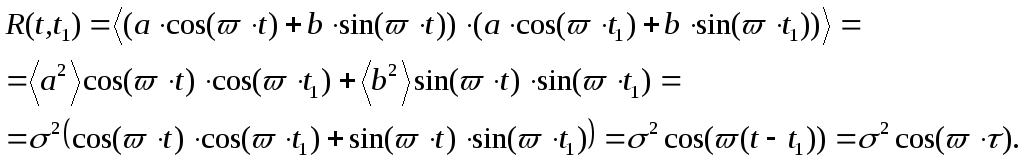
При выводе этого выражения было принято во внимание, что в силу независимости случайных величин a и b выполняется условие

.

Откуда учитывая, что для плотностей вероятности получим выражения

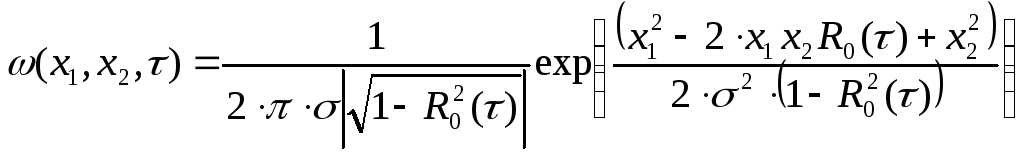
Задача

Найти характеристическую функцию для случайного стационарного процесса с плотностью вероятности

Ответ

Задача

На вход дифференцирующего устройства поступает случайный процесс с математическим ожиданием и корреляционной функцией .

Определите математическое ожидание и дисперсию на выходе системы

Ответ

Задача

Случайная величина х распределена равномерно в интервале найти закон распределения случайной величины .

Ответ

Функция в интервале монотонна поэтому плотность вероятности может быть найдена по формуле

Задача

Случайная величина х распределена равномерно в интервале найти закон распределения случайной величины .

Ответ

Функция в интервале немонотонна, поэтому плотность вероятности может быть найдена по формуле

Задача

При измерениях рабочего эталона массы (1 кг) получена следующая группа результатов наблюдений, г:

х1	х2	х3	х4	х5
999,998738	999,998699	999,998700	999,998743	999,998724
х6	х7	х8	х9	х10
999,998737	999,998715	999,998738	999,998703	999,998713

Обработкой результатов измерений, пользуясь правилами вычислений статистических характеристик при малом числе наблюдений, определите значение массы рабочего эталона и оцените результаты измерений.

Ответ Обработка результатов измерений заключается в вычислении ряда вспомогательных величин, приведенных в табл. 3.

ТАБЛИЦА 3

хi, г	хi0  106	 106	2 1012	4 1024
99998738	738	+ 17	289	83500
998699	699	-22	484	234300
998700	700	-21	441	198500
998743	743	+22	484	234300
998724	724	+3	9	00
998737	737	+16	256	65500
998715	715	-6	36	1300
998738	738	+17	289	83500
998703	703	-18	324	105000
998713	713	-8	64	4100
Сумма	7210	0	2676	1006000
Примечание. В графе 2 табл. 3 принято хi0 = Xi - 999,99800

Массу эталона принимают равной среднему арифметическому значению, определяемому по формуле

,

где п - число наблюдений.

В нашем случае х=999,99800 + х_iо = 999,998721 г.

Oценку среднего квадратического отклонения S(CKO) вычисляют по формуле

S =

Подставив в нее данные из графы 4 табл. 3, получим

S =  17 10^-6 г

Оценку среднего квадратического отклонения результата измерения определяют по формуле

=

Подставив числовые значения, получим

= = 5 10^-6 г.

Оценку СКО оценки СКО вычисляют по формуле

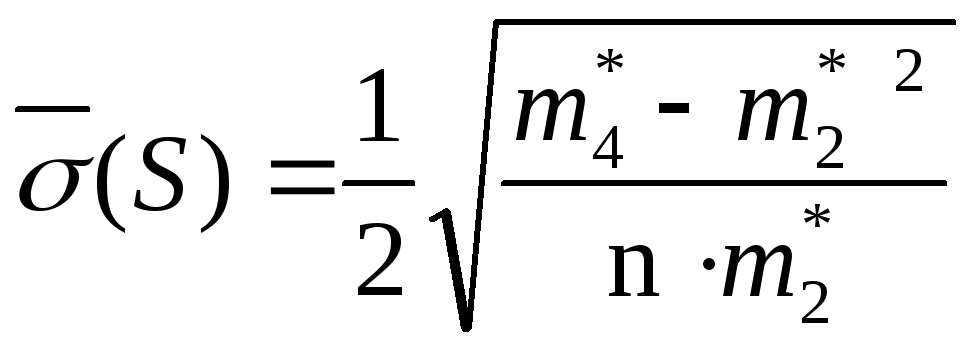
Предварительно вычисляют оценку четвертого момента и квадрат оценки второго момента распределения

= 100600 10^-24;

; ; т.е.

=1 10^-6 г.

Задача

Произведено измерение одной и той же длины L тремя различными способами различной точности: микрометром с погрешностью 0,01 мм, штангенциркулем с нониусом до 1/50 мм, штангенциркулем с нониусом до 1/10 мм и получены следующие результаты: 15,69 мм - микрометром; 15,66 мм - штангенциркулем до 1/50 мм; 15,70 мм - штангенциркулем до 1/10 мм.

Пользуясь понятием среднего взвешенного, запишите окончательный результат измерений.

Ответ. Критерием для установления весов в данном случае будет погрешность при- меняемых приборов. Самому малоточному прибору - штангенциркулю (1/10), имеющему погрешность 0,1 мм, приписываем вес, равный единице. Второму измерению (1/50) придаем вес, равный пяти, как имеющему погрешность в 5 раз меньшую, а первому результату, полученному с использованием вдвое более точного прибора, приписываем вес, равный 10. Для получения достоверного окончательного результата необходимо умножить каждый результат измерения на его вес, взять сумму полученных произведений и разделить на сумму весов:

,

т. е. L = 15,68мм.

Задача

Проведены три группы измерений сопротивления одной и той же образцовой катушки и получены следующие результаты, Ом: = 100,145 ± 0,005; =100,115 ± 0,20; = 100,165 ± 0,010.

Путем дальнейшей обработки результатов найдите погрешность среднего взвешенного.

Ответ. Результаты измерений для каждой группы записаны в виде средних значений и ± вероятных погрешностей результатов измерений в каждой из этих групп. В этом случае отношения весов обратно пропорциональны отношению квадратов вероятных погрешностей - средних квадратических отклонений (S₀), т. е.:

р₁ : р₂ : р₃ = = 40 000 : 2500 : 10 000 = 16 : 1 : 4.

В соответствии с полученным отношением, принимаем р₁ = 16; р₂ = 1; р₃ =4. Среднее взвешенное

Ом.

Для определения вероятной погрешности среднего взвешенного пользуются формулой

где p_i - вес каждого результата измерения ; _I - разность x_i - (-среднее взвешенное) ; п - число результатов измерений.

Для нашего случая: v_i=x₁ - = 100,115 - 100,147 = -0,002; v₂ = х₂ - = = 100,115- 100,147 = 0,032; v₃ = х₃ - =- 100,165 - 100,147=0,018; п = 3.

Тогда

Ом. Получаем возможность записать окончательный результат:

= (100,147± 0,005) Ом.

Погрешность среднего взвешенного меньше, чем погрешность любого из результатов.

Задача

При поверке дистанционного парогазового термометра класса точности 2,5 с пределом измерений 100° С были получены следующие показания образцовых ртутных термометров в оцифрованных точках поверяемого:

Поверяемые точки, 0 С	0	20	40	60	80	100
При повышении t,0 С	0,1	21	40	59	76	98
При понижении t, 0 С	0	22	41	60	77	98

Оцените годность прибора.

Ответ. Прибор класса точности 2,5 на 100°С должен иметь абсолютную допускаемую погрешность 2,5 °С (или 2,5 деления шкалы в 100 отметок). В точке 80°С прибор имеет максимальную погрешность 4°С и поэтому должен быть забракован.

Задача

Оцените годность пружинного манометра класса точности 1,0 на 60 кПа, если при его поверке методом сличения с образцовым манометром класса точности 0,2 в точке 50 кПа при повышении давления было зафиксировано 49,5 кПа, а при понижении 50,2 кПа.

Ответ. Вариация показаний пружинного манометра не должна превышать основной погрешности. В нашем случае манометр класса точности 1,0 может иметь абсолют- ную погрешность  = (А_к)/100 = (1  60) /100 = 0,6 кПа. Это же значение может иметь и вариация показаний b.

Для нашего манометра:

b = A_б -А_м,

где _б и _м - абсолютная погрешность при подходе к поверяемой точке со стороны больших и меньших значений, соответственно; А_б и А_м - показания образцового прибора в этих точках, т. е. b = 0,7 кПа.

Следовательно, b  , так как 0,7 кПа > 0,6 кПа.

Манометр должен быть забракован несмотря на то, что погрешности в точке 50 кПа не превышают допускаемую: (0,2 < 0,6 и 0,5 < 0,6).

Задача

Микроамперметр на 100 мкА имеет шкалу в 200 делений.

Определите цену деления и возможную погрешность в делениях шкалы, если на шкале прибора имеется обозначение класса точности 1,0.

Ответ. Цена деления С = 100/200 = 0,5 мкА.

Допускаемая погрешность  = 1 мкА или 2 деления шкалы.

Задача

Для аналоговых электроизмерительных приборов установлены классы точности 0,05; О1; 0,2; 0,5; 1; 1,5; 2,5 и 4.

Определите их соотношения попарно. Сделайте заключение: какие приборы могут использоваться в качестве образцовых?

Ответ. 2; 2; 2,5; 2; 1,5; 1,7; 1,6.

Закономерности в этом ряде нет, рядом стоящие по классу приборы не могут быть образцовыми по отношению к другому. Для образцовых и лабораторных электроизмерительных приборов (ЭИП) это соотношение, как правило, должно быть 1:5, для щитовых ЭИП 1 : 4.

5. Для пружинных манометров установлены классы точности 0,15; 0,25; 0,4; 1; 1,6; 2,5; 4; 6,3; 10.

На каком принципе построен этот ряд?

Ответ. Допускаемые погрешности, установленные для манометров, подчиняются ряду предпочтительных чисел со знаменателем, приблизительно равным 1,6.

Задача

Вы приобрели весы, в паспорте которых указано, что они класса точности 3.

Назовите допускаемую погрешность весов.

Ответ. У весов класс точности определяет значение допускаемой погрешности (в процентах) при наибольшей нагрузке весов и обозначается одной из цифр от 0 до 5 со следующей за ней буквой а, б или в. Цифры обозначают число десятичных знаков после запятой, а буквы соответствуют значащим цифрам 1, 2, 5, т. е. в нашем примере допускаемая погрешность весов составляет ±0,002%.

Задача

Чем отличается для мер длины класс точности от разряда?

Ответ. Класс точности зависит от отклонения срединной длины меры от номинального размера (это 0, 1, 2, 3, 4 и 5-й классы); разряд же (1, 2, 3, 4 и 5-й) - от точности определения (аттестации) срединной длины, выражаемой погрешностью действительного значения срединной длины.

Задача

При изготовлении наборов гирь, магазинов сопротивлений и других мер в каждом десятичном числовом разряде можно иметь ряд 1; 2; 3; 4 или 1; 2; 2; 5. Оба ряда дают возможность воспроизвести все значения от 1 до 10.

Какой из рядов более рационален?

Ответ. Более рационален ряд 1; 2; 2; 5, так как он состоит из трех номиналов, что выгодно при массовом производстве и создает удобство пользования этим набором (в ряде 1; 2; 3; 4 меры 2 и 3, а особенно 3 и 4, не очень заметно отличаются по размерам, что усложняет пользование ими).

Задача

Какая закономерность есть в установлении пределов измерений щитовых вольт- метров, амперметров?

Ответ. Пределы измерения выбирают из ряда В = а • 10ⁿ, где В - предел измерения; а - коэффициент, зависящий от измеряемой величины, и в нашем случае равный 1;

1,25; 1,5; 2; 2,5; 3; 4,5; 6; 7,5; 8; п - любое положительное или отрицательное число или нуль.

Задача

При поверке амперметров и вольтметров в последнее время все чаще используется метод прямых измерений - поверка этих приборов осуществляется с помощью калибраторов тока и напряжения. Приведенную погрешность, %, поверяемого прибора в этом случае вычисляют по формуле

 = 100,

где Х_П - значение для поверяемой отметки шкалы прибора; Хд - действительное значение, воспроизводимое калибратором; X_Т - нормируемое значение для поверяемого прибора.

Какие нормируемые значения берутся и в зависимости от чего?

Ответ. Нормируемые значения берутся для приборов с равномерной или степенной шкалой в зависимости от расположения на шкале нулевой отметки: если нулевая отметка находится слева (в начале шкалы - рис. 28), то X_N берется равным конечному значению шкалы, если нулевая отметка внутри шкалы (рис. 29), то X_N берется равным арифметической сумме конечных значений. Так, X_N = 6 А - для амперметра с диапазоном измерения от - 3 А до + 3 А (см. рис. 29).

РИС. 28

РИС. 29