Практическое занятие № 14 Тема занятия «Предел функции. Основные теоремы о пределах»

Цель занятия: Введение понятия предел функции, формирование навыков вычисления пределов.

Организационная форма занятия: практикум-тренинг.

Компетенции, формируемые на занятии: ОК-1, ПК-2.

При формировании на занятии названных компетенций специалист должен знать основополагающее понятие математического анализа предела функции; уметь использовать это понятие в других областях математического знания и дисциплинах естественнонаучного содержания; владеть техникой вычисления пределов.

Вопросы, выносимые на обсуждение

1. Определение предела функции.

2. Основные теоремы о пределах.

3. Предел функции на бесконечности.

4. Односторонние пределы.

Методические рекомендации

Для подготовки к занятию дома

1. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.

2. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.

3. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.

4. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.

5. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

На занятии по указанию преподавателя

1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

Дома закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома. Подготовьтесь к самостоятельной работе №6 по теме «Предел функции», примерный вариант самостоятельной работы вы можете найти в программе дисциплины.

Рекомендуемая литература

[1] глава 7 пп. 7.3. - 7.5.

[2] глава VI §§ 4 – 5 .

[3] глава 4 § 18.

[4] часть II занятия 14 – 17.

[5] глава 1 § 1.2.

[6] глава 4 §§ 2 – 6.

[7] глава IV §§ 2 – 6.

[8] глава 4 §§ 2 – 6.

Примеры решения типовых задач

Найдите пределы:

1. .

Решение. Так как и , то мы имеем неопределенность 0/0. Раскроем ее, разложив числитель и знаменатель на множители и упростив дробь:

.

2. .

Решение. Так как и , то имеем неопределенность . Для ее раскрытия умножим числитель и знаменатель дроби на выражение сопряженное числителю:

3. а) ; б) ; в) .

Решение. В каждом из пределов имеем неопределенность вида . Для ее раскрытия числитель и знаменатель разделим на старшую степень знаменателя:

а) ,

т.к.

б)

в)

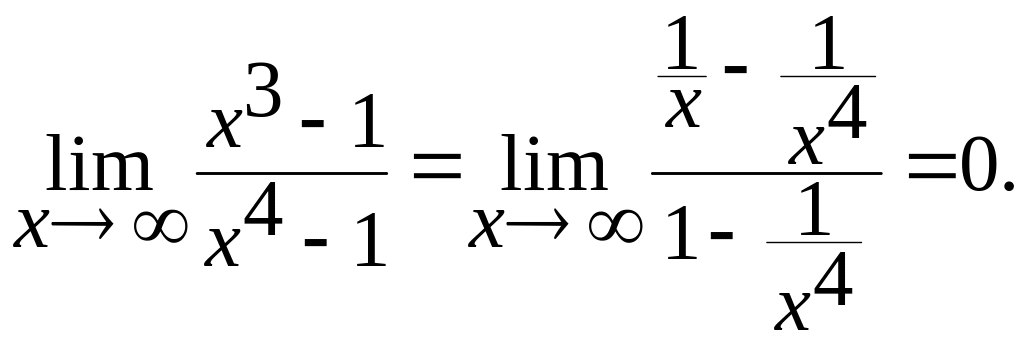
Замечание. Если числитель и знаменатель дроби есть многочлен, то предел дроби при равен:

а) отношению коэффициентов при старших степенях, если старшая степень числителя равна старшей степени знаменателя;

б) бесконечности, если старшая степень числителя выше старшей степени знаменателя;

в) нулю, если старшая степень числителя меньше старшей степени знаменателя.

4. Вычислите односторонние пределы:

а) ; б) .

Решение. а) Если , то , а следовательно , или .

б) Если , то , следовательно , т.е. .