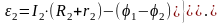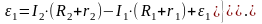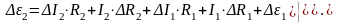Московский государственный университет путей сообщения рф (миит) Кафедра «Физика-2»

Группа_______УЭМ-122 ____________ _ К работе допущен____________________

(Дата, подпись преподавателя)

Студент ___________Попова Н.В __ Работа выполнена___________________

(ФИО студента) (Дата, подпись преподавателя)

Преподаватель________ ___ Отчёт принят_______________________ (Дата, подпись преподавателя)

Отчёт по лабораторной работе №______18__

ЗАКОНЫ РАЗВЕТВЛЕННЫХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

(Название лабораторной работы)

1. Цель работы:

Измерение силы тока в узле разветвлённой цепи.Определение ЭДС источников тока и разности потенциалов с использованием общего закона ОМА . ____________________________________________________________________

2. Принципиальная схема установки (или её главных узлов):

3. Основные теоретические положения к данной работе (основополагающие утверждения: формулы, схематические рисунки): Для характеристики электрического тока в электрических цепях используют понятие силы тока и плотности тока. Сила стационарного электрического тока есть алгебраическая ве­личина, равная заряду, протекающему через некоторую по­верхность, в единицу времени. Если за время dt через поверх­ность проводника переносится заряд dq, то

За положительное направление тока принято направление движения положительных зарядов. Плотность тока - вектор­ная величина, численно равная силе тока, протекающего через единичную площадку, перпендикулярную скорости дви­жения зарядов:

где dl—сила тока, протекающего через площадку dS₁. Век­тор плотности тока совпадает по направлению с вектором скорости положительно заряженных частиц. Связь силы тока и плотности тока может быть записана в виде интеграла по поверхности S, через которую течет ток:

То есть сила тока равняется потоку плотности тока через по­верхность S. Здесь  - угол, образованный вектором плотно­сти тока и нормалью к элементу поверхности ds

В зависимости от величины  сила тока может иметь положительный или отрицательный знак.

24

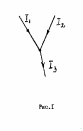Одним из элементов разветвленной цепи является узел - место соединения трех и более проводников (рис. 1).

Поскольку в цепях постоянного тока нигде не происходит накапливания электрического заряда, а также его возникновения или уничтожения (закон сохранения заряда), то заряд, приходящий в единицу времени к узлу, равен заряду, уходя­щему за это же время от узла. Из этого следует первое пра­вило Кирхгофа для цепей постоянного тока: алгебраическая сумма сил токов, сходящихся в узле, равна нулю:

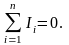
При составлении уравнений с использованием этого пра­вила токи, текущие к узлу, считают положительными, а токи, текущие от узла - отрицательными.

Свободные носители заряда в проводнике (электроны, ионы) при движении испытывают сопротивление. В металле, например, электроны взаимодействуют с ионами кристалличе­ской решетки и теряют свою энергию. Поэтому ток в провод­нике поддерживается только при условии непрерывного действия на электроны ускоряющего электрического ноля.

Между плотностью тока и напряженностью электрического поля в каждой точке проводника существует зависимость:

(1)

где удельная электропроводность вещества.

Эту формулу называют законом Ома в дифференциальной форме. Рассмотрим этот закон подробнее. Существование на­пряженности электрического поля указывает на изменение потенциала вдоль проводника. Следовательно, условием существования электрического тока на участке цепи является наличие разности потенциалов на концах этого участка.

Один из источников создания электрического поля внутри проводника - избыточный положительный или отрицательный заряд, накапливающийся в некоторых участках проводника. Но этo поле, имеющее электростатическое

происхождение, одно не может поддерживать в цепи постоянный электрический ток, т.к. электростатические силы способствуют сближению разноименных зарядов и выравниванию потенциала проводника. Для поддержания постоянного тока в цепи, в ней на некото­рых участках должны существовать силы неэлектростатиче ского происхождения. Эти силы поддерживают такое распре­деление зарядов в проводниках, которое создает внутри них поле с напряженностью, не равной нулю. При этом на неко­торых участках цепи силы неэлектростатического происхож­дения заставляют свободные носители зарядов двигаться про­тив поля, вызванного электростатическими силами.

Силы неэлектростатического происхождения называют сторонними. Они могут быть обусловлены химическими про­цессами, диффузией носителей зарядов в неоднородной среде или через границу двух разнородных веществ, явлением элек­тромагнитной индукции и т. д. С учетом всех сил, действующих на заряды, формулу (1) записывают в более общем виде:

(2)

Иными словами, в уравнении (1)

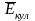здесь - напряженность поля сторонних сил, т. е. си­ла неэлектростатического происхождения, действующая на пробный единичный положительный заряд, - напряжен­ность поля кулоновских сил.

Сторонние силы в практике удобно характеризовать не напряженностью, а работой, которую они совершают при переносе единичного положительного заряда. Эта работа назы­вается электродвижущей силой (ЭДС), обозначается буквой  и может быть выражена в виде интеграла, начало и конец которого обозначен соответственно 1 и 2:

(3)

где dl – элемент проводника с током.

На основании равенства (2) запишем интеграл для участка 1-2:

(4)

где 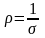- удельное сопротивление проводника.

Предположим, что ток течет по прямолинейному однород­ному проводнику и на участке 1-2 постоянен. Вынесем  за знак интегралов в правой части уравнения. Разделим последнее равенство на . В правой части полученного равенства первое слагаемое есть разность потенциалов на концах участ­ка 1-2:

(5)

а второе—ЭДС на этом участке:

(6)

Подставим уравнения (5) и (6) в уравнение (4) н учтем, что вектор 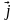совпадает по направлению с . Учитывая, что поперечное сечение проводника S₁ перпендикулярно этим векторам, уравнение (4) примет вид:

(7)

здесь

(8)

а I – сила постоянного тока, и получим:

(9)

27

Здесь 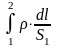- сопротивление участка 1-2.

Тогда (9) примет вид:

(10)

Полученное уравнение носит название закона Ома для участка цепи, содержащего ЭДС.

Иногда его записывают в виде:

(11)

и

Рис. 1

называют обобщенным законом Ома.

При записи этого уравнения применяется правило знаков которое утверждает, что, если направление токов совпадает- с направлением обхода участка цепи 1—2, ток в уравнении (11) считается положительным. Если в направлении обхода участка от точки 1 к точке 2 потенциал источника _ повы­шается, то ЭДС берется с плюсом, в противном случае— с минусом.

Описание эксперимента

В лабораторной работе используется электрическая цепь, состоящая из трех ветвей, в каждую из которых включен ис­точник тока, сопротивление, микроамперметр, переключатель.

Источники тока включаются в цепь с помощью переклю­чателей П_1, П₂, П₃, которые позволяют менять направление сторонних сил и, соответственно, знак ЭДС в цепи. Знак ЭДС определяется правилом знаков, описанным во введении к дан­ной лабораторной работе.

Пусть выбранным направлением считается направление от узла 1 к узлу 2 (см. рис. 2), тогда, если н этом направлении потенциал источника ЭДС возрастает, то  >0. и в против­ном случае—наоборот, <0.

Для каждой из трех ветвей запишем обобщенный закон Ома. Например, для ветви 1:

,

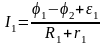где R₁ — сопротивление, r₁ — общее сопротивление источника тока _ и амперметра A₁.

В написанном равенстве и во всех последующих будем считать _, _, _ — алгебраическими значениями ЭДС.

Из уравнения (11) получаем:

.

(12)

Разность потенциалов на других ветвях также равна (_-__Напишем для них

,

(13)

где r₂ и r₃ —общие сопротивления, соответственно, источ­ника тока _ и амперметра A₁Из выражения (10) получим:

(14)

Пусть _ и все значения сопротивлений известны, тогда, измерив значения сил тока в цепи, можно рассчитать (__) по равенству (12), а затем _ и _ пo формулам (14).

29

Порядок выполнения работы

1. Собрать схему, предварительно разомкнув все переклю­чатели. Проверить и отрегулировать нулевое положение стре­лок микроамперметров.

2. Замкнуть все переключатели в положение «а». Записать в таблицу 1 показания микроамперметров с учетом знака силы тока. Токи считаются положительными при отклонении стрелки приборов направо от нуля и отрицательными—при отклонении налево от нуля.

3. Изменять включение _, _, _ меняя положение пере­ключателей П₁, П₂, П₃ в соответствии с порядком, указанным в таблице 1. Каждый раз записывать показания микроамперметров с учетом знака силы тока.

4. Вычислить значения силы тока в микроамперах и для каждого положения переключателей найти алгебраическую сумму сил токов.

5. Определить абсолютные ошибки I₁, I₂, I₃ при изме­рении силы тока, обусловленные конструкцией приборов. Вы­числить ошибку в определении суммарного тока но формуле:

I₁I₂ I₃) = I₁ +I₂ +I₃.

В этом соотношении все I нужно брать по абсолютному значению. Сравнить полученное значение алгебраической сум­мы сил токов в узле с величиной суммарной ошибки.

6. Используя известное значение ₁ и значения сопротив­лений участков цепи, найти для каждого варианта включения разность потенциалов (__) по формуле (12) и электро­движущие силы ₂ и ₃ по формулам (14). Полученные значения с учетом знака записать в таблицу I. Учесть, что при переключении переключателей меняются знаки ЭДС.

7. Рассчитать абсолютную ошибку косвенных измерений. Преобразуем формулу (14), подставив в нее выражение- для определения разности потенциалов, полученное из фор­мулы (12):

(15)

При условии, что погрешностями r можно пренебречь ввиду их малости, получим формулы для расчета абсолютных погрешностей косвенных измерений:

4. Таблицы и графики¹.

№ п.п.

Положение переключателей

I1

I2

I3

, В

, В

, В

П1

П2

П3

дел.

мкА

дел.

мкА

дел.

мкА

1

а

а

а

2

а

а

б

3

а

б

а

4

а

б

б

5

б

а

а

6

б

а

б

7

б

б

а

8

б

б

б

среднее

Таблица №1
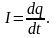
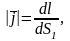
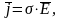
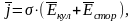
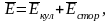
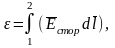
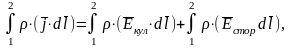
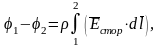
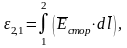
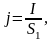
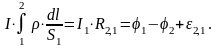
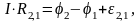
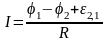
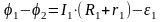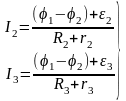