2.2.2. Поверхневий натяг

Молекули рідини розташовані настільки близько одна до одної, що сили притягання між ними мають значну величину. Оскільки взаємодія швидко зменшується з відстанню, починаючи з деякої відстані силами притягання між молекулами можна знехтувати. Ця відстань r називається радіусом молекулярної дії, а сфера радіуса r називається сферою молекулярної дії.

Молекули поверхневого шару рідини перебувають в особливому енергетичному стані порівняно з молекулами об’єму рідини. Справді, для переведення молекул рідини з її об’єму на поверхню, тобто для збільшення поверхні рідини, потрібно виконати роботу сил внутрішнього тиску. Суттєвим при цьому є характер процесу, при здійсненні якого робота, виконувана зовнішніми силами над системою (рідиною), повністю йшла на переведення молекул рідини з об’єму в поверхневий шар. Таким процесом повинен бути оборотний ізотермічний процес, а характеристичною термодинамічною функцією повинна стати вільна енергія - . Отже:

, (1)

- питома вільна поверхнева енергія (коефіцієнт поверхневого натягу),

dS – площа елемента поверхні рідини (dS>0).

Знак „-” показує, що робота виконується зовнішніми силами над системою.

У стані стійкої рівноваги надлишкова поверхнева потенціальна енергія рідини повинна бути мінімальною. Тому рідина, на яку не діють зовнішні сили, за умови її практичної нестисливості має набрати форми сфери. Отже, сили поверхневого шару повинні зумовлювати тенденцію рідини зменшити свою поверхню.

Такий „силовий” підхід до описання поверхневих явищ потребує введення сил, що намагаються зменшувати поверхню рідини. Ці сили повинні бути напрямлені по дотичних до поверхні рідини..

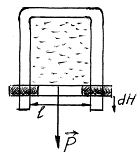
Рис. 1

Якщо дротяний контур з рухливою перетинкою помістити в мильний розчин, то він затягнеться мильною плівкою. Сили поверхневого натягу, якщо перетинка досить легка, намагатимуться скоротити поверхню рідини і перетинка почне підніматися вгору. У разі зрівноваження сил поверхневого натягу і тяжіння, перетинка перебуватиме в рівновазі.

Тоді:

2F=P (оскільки плівка має дві поверхні),

F – сила поверхневого натягу;

P - сила тяжіння.

Якщо під дією сили F перетинка перемістилася на відстань dh, то робота, виконана нею:

.

Тоді:

. (2)

Таким чином, коефіцієнт поверхневого натягу можна визначити як величину, що чисельно дорівнює силі, яка діє по дотичній до поверхні рідини і припадає на одиницю довжини лінії – границі рідини.

2.2.3. Явища на межі рідини і твердого тіла

Тверді тіла, як і рідкі, мають поверхневий натяг. При розгляді явищ на межі розділу різних середовищ слід враховувати, що поверхнева енергія рідини чи твердого тіла залежить не лише від властивостей даної рідини чи твердого тіла, але й від властивостей тієї речовини, з якою вони межують. Строго кажучи, потрібно розглядати сумарну поверхнева енергію двох межуючих одна з одною речовин. Лише якщо одна речовина газоподібна, хімічно не реагує з іншою речовиною і малорозчинна в ній, можна говорити про коефіцієнт поверхневого натягу другого рідкого чи твердого тіла.

Рис. 2

Якщо межують одна з одною одразу три речовини: тверда, рідка і газоподібна, то вся система приймає конфігурацію, що відповідає мінімуму сумарної енергії (поверхневої, в полі сил тяжіння і т.п.).

Рис. 3

Зокрема контур, по якому межують всі три речовини, розташований на поверхні твердого тіла таким чином, щоб сума проекцій всіх, прикладених до кожного елемента контуру сил поверхневого натягу на напрямок, в якому елемент контуру може переміщуватись (тобто на напрямок дотичний до поверхні твердого тіла), дорівнювала нулю.

Маємо умову рівноваги елемента контуру довжиною (з малюнка):

. (3)

де - коефіцієнти поверхневого натягу на межах: тверде тіло-газ, тверде тіло-рідина, рідина-газ.

Кут між дотичними до поверхні твердого тіла і до поверхні рідини,(що відраховується всередині рідини) називається крайовим кутом (з рівняння (3)).

. (4)

Крайовий кут визначається цим виразом лише за умови, що:

. (5)

Якщо ця умова не виконується ні при якому значенні не може встановитися рівновага. Це має місце в двох випадках:

1. .

Рис. 4

Яким би малим не був кут , сила переважує дві інші. В цьому випадку рідина необмежено розтікається по поверхні твердого тіла – має місце повне змочування.

Заміна поверхні тверде тіло-газ двома поверхнями, тверде тіло-рідина і рідина-газ, виявляється енергетично вигідно

.

2. .

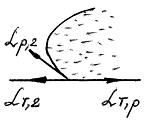
Рис. 5

Якби не був близький до π , сила , переважає дві інші.

Поверхня, по якій рідина межує з твердим тілом, стягується в точку, рідина відхиляється від твердої поверхні – має місце повне незмочування. Заміна поверхні тверде тіло-рідина двома поверхнями тверде тіло-газ і рідина-газ, виявляється енергетично-вигідно

.

При виконанні умови (5), крайовий кут може виявитися гострим чи тупим в залежності від співвідношення .

Якщо ,кут - гострий. В цьому випадку має місце часткове змочування. Якщо , кут - тупий. Має місце часткове незмочування.

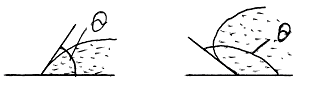
Рис. 6