4. Обертальний рух твердого тіла

Лекція 5

4.1. Момент сили. Момент імпульсу

4.1.1. Тверде тіло як система матеріальних точок

Розміри і форма тіл не грають важливої ролі. Але у ряді випадків цими розмірами не можна знехтувати, бо розміри і форма тіл визначають характер руху. Якщо при цьому деформаціями тіла можна знехтувати, то дане тіло – тверде.

При вирішенні питань механіки твердого тіла завжди можемо розділити тверде тіло на окремі елементи так, щоб розміри і форма кожного не грали ролі при розгляді його руху. При цьому, для того, щоб знайти рівняння руху твердого тіла, не потрібно знати внутрішні сили, які діють в тілі, бо сума усіх внутрішніх сил, що діють в системі матеріальних точок дорівнює нулю.

При вивченні руху твердого тіла, ми розглядатимемо ті рухи, при яких швидкість усіх елементів мала порівняно з швидкістю світла, і тому маси усіх елементів тіла вважатимемо незалежними від швидкості їх руху.

Будь-який рух можна представити як суму обертального і поступального.

4.1.2.А. Момент сили і пари сил відносно точки

Так як обертати тіло можна навколо точки і навколо осі, то розрізняють момент сили(імпульсу) відносно точки і відносно осі.

Рис. 1

Момент сили відносно точки – добуток сили на найкоротшу відстань від цієї точки до лінії дії цієї сили:

. (1)

Момент сили – векторна величина. В загальному випадку виражається векторним добутком:

. (2)

Розкладемо силу на 2 складові: колінеарну і тангенційну . Колінеарна і тангенційна складові перпендикулярні між собою.

Виразимо момент сили відносно т.О через ці дві величини:

Так як радіус-вектор паралельний з вектором сили, то:

,

тому:

. (3)

Модуль моменту сили визначається:

. (4)

Момент кількох сил, що мають однакову точку прикладання, визначається:

. (5)

Якщо маємо випадок, коли існує момент кількох сил, що мають різні точки прикладання, то результуючий момент сили:

. (6)

Парою сил називаються дві прикладені до одного і того ж тіла рівні по величині і протилежно-направлені сили, з неспівпадаючими лініями дій.

Рис. 2

Знайдемо момент пари сил відносно т.О. Момент пари сил дорівнює сумі моменту сили 1 і моменту сили 2:

.

За означенням моменту сили: , тоді

.

При цьому, з малюнка: , тоді

.

Так як ці дві сили направлені у різні сторони, то за 3-ім законом Ньютона:

,

тоді результуюча моменту сили:

. (7)

Момент пари сил відносно точки не залежить від положення точки відносно пари сил.

Модуль моменту пари сил відносно точки дорівнює добутку сили на плече сили:

. (8)

4.1.2.Б. Момент сили відносно осі

Нехай на тіло закріплене віссю Z діє направлена сила F, тоді дане тіло може обертатися тільки навколо осі Z.

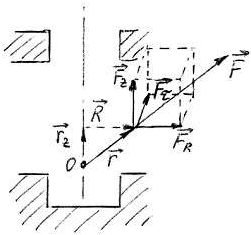
Рис. 3

Знайдемо момент сили відносно деякої т.О, що лежить на осі обертання, а потім виділимо складову моменту сили відносно осі Z, яка буде паралельна осі Z.

,

тоді момент сили відносно осі Z:

.

Так як векторний добуток дає вектор, перпендикулярний до осі Z і до , то проекція вектора на вісь Z дорівнює нулю, тоді:

.

Розкладемо силу на 3 складові: радіальну, тангенціальну, колінеарну, тоді:

.

Якщо підставимо значення сили у формулу , то отримаємо:

.

У рівнянні другий доданок дорівнює нулю так як вектори і паралельні, перший також дорівнює нулю, так як перпендикулярний до осі Z, таким чином:

. (9)

Отже тільки одна складова сили(тангенційна) має змогу обертати тіло навколо осі Z.

- момент сили відносно осі обертання Z.

Якщо на тіло подіють кілька сил, то повний момент сил обертання дорівнює векторній сумі моментів усіх сил:

. (10)