5. Коррекция систем наведения методом лах.

В задании требуется провести синтез последовательного корректирующего устройства методом логарифмических частотных характеристик (структурная оптимизация системы) по заданным времени переходного процесса t_пп, величине перерегулирования %. Точность оценивать для входного сигнала вида . Ошибка  должна не превышать половины ошибки ^*, полученной при параметрической оптимизации из предыдущего раздела. Найти передаточную функцию последовательного корректирующего устройства W_пку(р) и рассчитать его электрическую схему.

В случае последовательной коррекции звено с передаточной функцией W_пку(р) включается в прямую цепь рассматриваемой системы. При этом должна обеспечиваться желаемая передаточная функция разомкнутой системы , которая в этом случае имеет вид

, (40)

где - передаточная функция располагаемой разомкнутой системы (разомкнута только главная обратная связь) , полученная после проведения параметрической оптимизации. Тогда ЛАФЧХ (сокращенно ЛАХ) имеют вид:

(41)

где

(42)

Из (41) следует

(43)

Из выражения (43) следует, что ЛАХ последовательного корректирующего устройства можно определить путем графического вычитания ординат ЛАХ располагаемой части системы из ординат желаемого ЛАХ.

Тогда синтез последовательного корректирующего устройства осуществляется следующим образом:

• строится ЛАЧХ ЛФЧХ располагаемой части системы;

• выбирается тип ЖЛАЧХ и строится

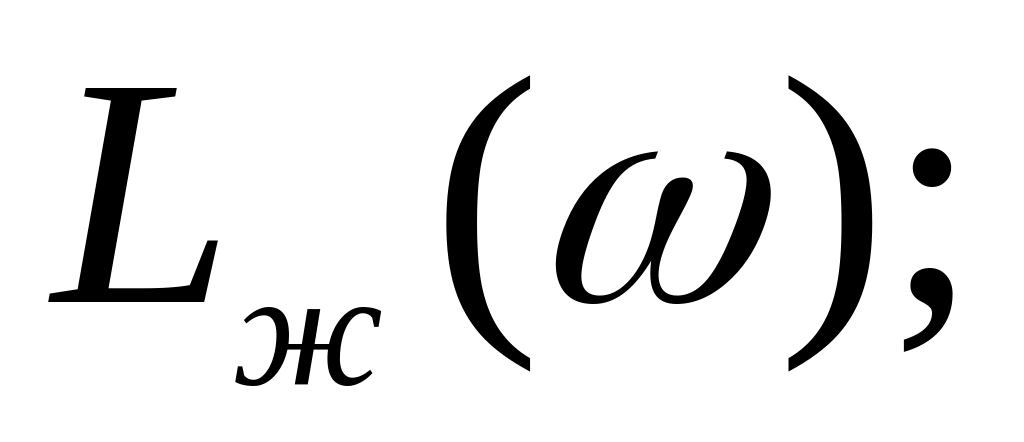
• строится ЛАЧХ корректирующего устройства по формуле (43);

• выбирается тип пассивного контура по табл. из приложения, определяются постоянные времени, коэффициенты усиления.

Построение ЛАЧХ располагаемой части системы осуществляется методом асимптотических ЛАХ. В этом случае передаточная функция располагаемой части системы (обычно обладающая астатизмом первого порядка) должна быть приведена к виду (при отсутствии колебательных звеньев)

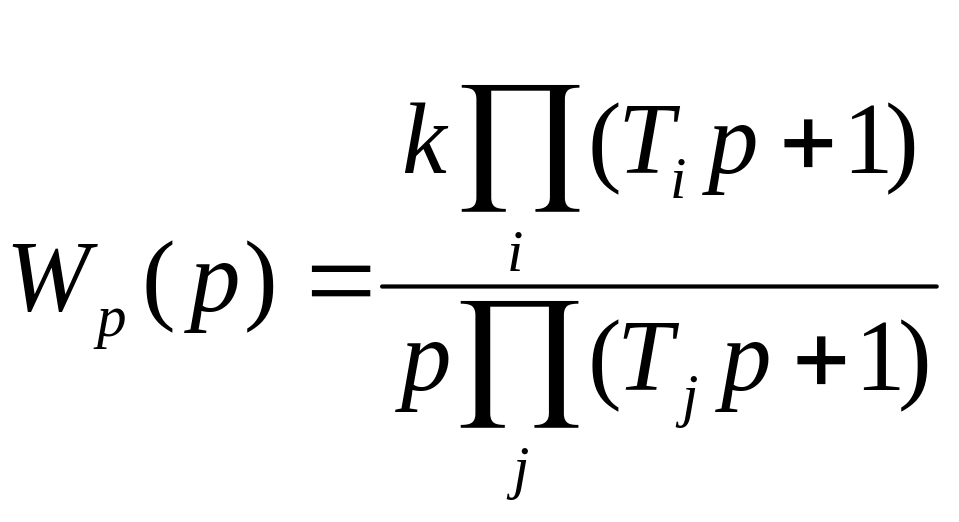. (44)

Постоянные упорядочиваются по мере убывания ( ) и вычисляются сопрягающие частоты ( ), которые соответственно упорядочены по возрастанию. Если все сопрягающие частоты больше единицы (что обычно имеет место для приводов), то на частоте (соответственно, ) откладывается ордината , через которую проводится прямая с наклоном -20 дб/дек. до первой сопрягающей частоты, после чего наклон изменяется на  20 дб/дек в зависимости от того находится ли звено с этой частотой в числителе или знаменателе располагаемой ПФ. Если первая сопрягающая частота меньше 1, то вычисляется значение , которое и откладывается на первой сопрягающей частоте. Дальнейшая процедура аналогично, за исключением того, что начальный наклон ЛАХа изменяется на этой частоте.

Построение желаемой ЛАЧХ системы в значительной степени зависит от постановки задачи и требованиям по точности и по качеству. В данном случае построение осуществляется в следующей последовательности:

• в области низких частот на частоте входного воздействия 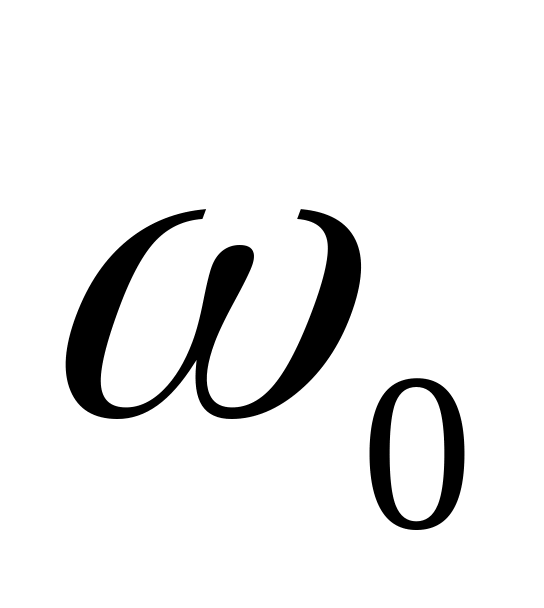откладывается контрольная точка 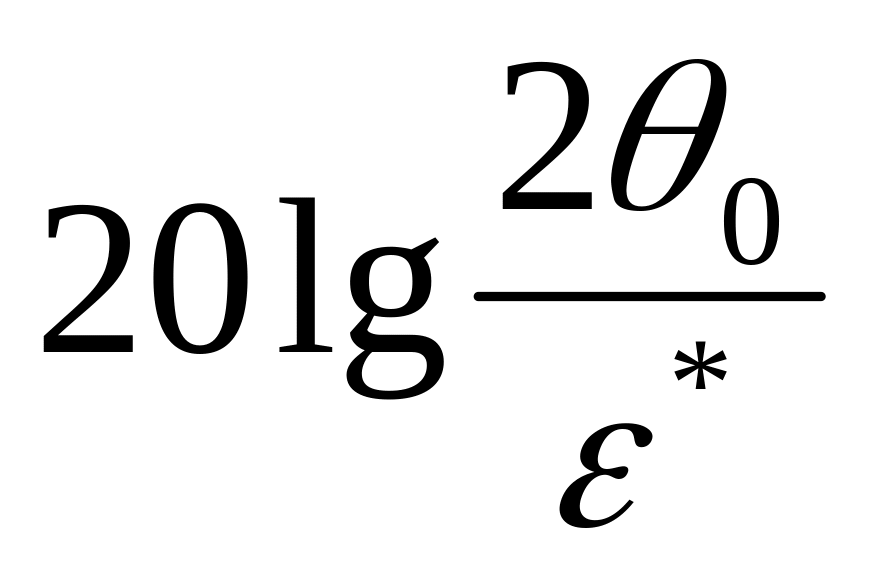, где - значение ошибки полученной в результате параметрической оптимизации. Поднимаем располагаемый ЛАХ выше контрольной точке (т.е. принимаем k в передаточной функции располагаемой системы равным 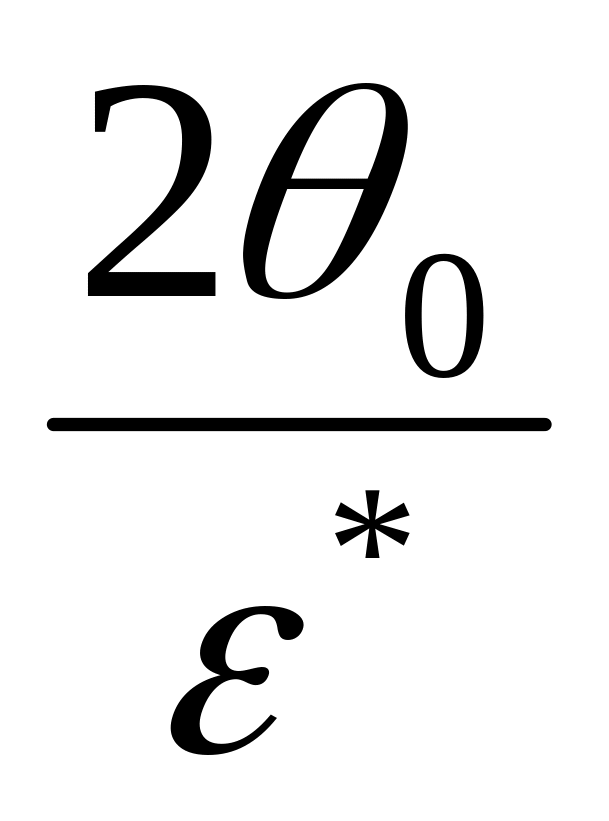), если ЛАХ проходил выше, то оставляем его без изменения.

• в области средних частот, в зависимости от требуемого времени переходного процесса t_пп и величины перерегулирования , по номограмме, приведенной на рис.15 , определяется частота среза системы _с .

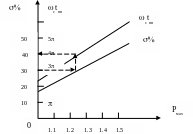
Рис.15.

На рисунке показано как определить _сt_пп для =30. Тогда для заданного t_пп вычисляется _с. Через точку на оси абсцисс проводится прямая с наклоном -20 дб/дек. Затем осуществляется сопряжение низкочастотного и среднечастотного участков желаемого ЛАХа. Для этого на частоте контрольной точки увеличиваем наклон располагаемого ЛАХа на -20дб/дек (-40дб/дек) и проводим прямую (через контрольную точку) до пересечения с прямой среднечастотного участка.

• в области высоких частот среднечастотный участок желаемого ЛАХа обычно переходит в высокочастотный располагаемого, что обеспечивает более простую реализацию корректирующего устройства.

Пример 6. Синтез корректирующего устройства методом ЛАХ.

Передаточная функция разомкнутой располагаемой части системы имеет вид

. Требуется определить передаточную функцию последовательного корректирующего устройства, обеспечивающего ошибку не больше рад при входном сигнале , перерегулирование не более 30, время переходного процесса не более 1 сек.

1. Строим ЛАХ располагаемой системы, пунктирная линия на рис.16. Постоянные времени 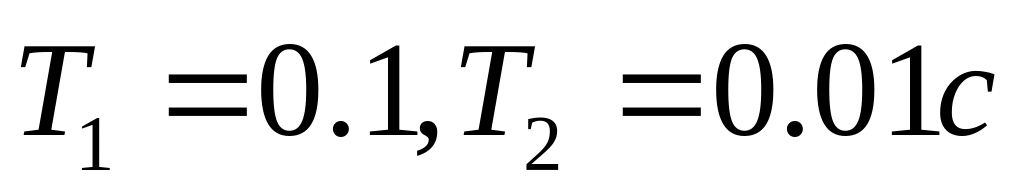, тогда сопрягающие частоты 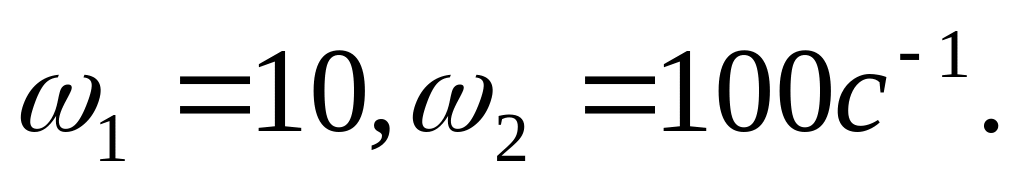Ордината .

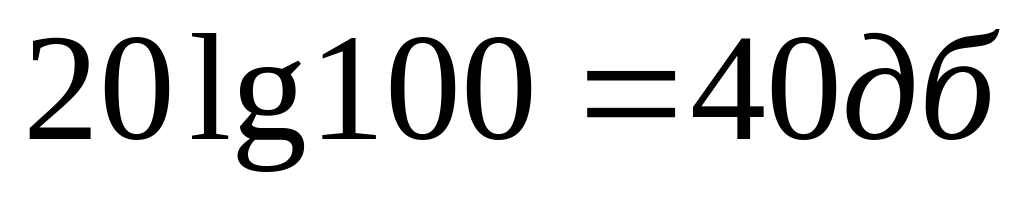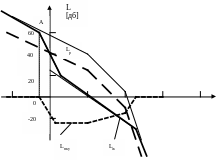
1 2 3 4

Рис.16.

2. Строим желаемую ЛАХ. На частоте lg0.628 = -0.2 откладываем ординату

, точка А. Поднимем располагаемый ЛАХ выше этой точки. Теперь низкочастотная часть располагаемого и желаемого ЛАХа совпадают.

По номограмме приведенной на рис.15 определяем, что для заданного  =30,

_сt_пп = 4. Тогда для t_пп = 1с., _с = 12.56с^-1, а lg12.56 = 1.1. Откладываем эту точку на оси абсцисс и проводим через нее прямую с наклоном -20дб/дек до пересечения с располагаемой ЛАХ в области высоких частот.

Сопрягаем низкочастотный и среднечастотный участки желаемойЛАХ. Для этого из точки А проводим прямую с наклоном -60 дб/дек (наклон -40дб/дек не дает пересечения с прямой среднечастотного участка в области частот меньшей частоты среза) до пересечения с прямой желаемой ЛАХ в области средних частот. Полученная желаемая ЛАХ выделена жирной линией.

3. Строим ЛАХ корректрующего устройства L_пку. Для этого из желаемой ЛАХ вычитаем располагаемую, рис.16. Полученная ЛАХ выделена точечным пунктиром.

В соответствии с рисунком передаточная функция корректирующего устройства имеет вид

,

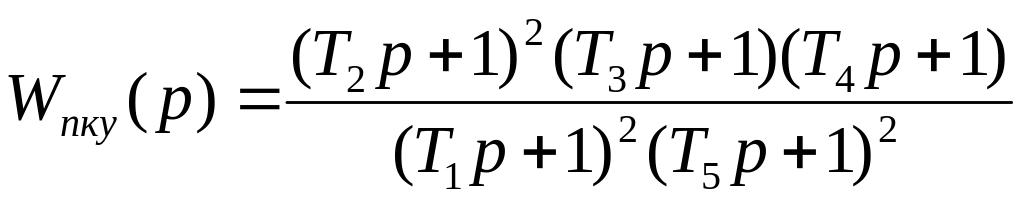где постоянные времени и соответствующие им сопрягающие частоты имеют значения: Т₁ = 1.59 с, Т₂ = 0.95 с, Т₃ =0.1 с, Т₄ = 0.01 с, Т₅ = 0.00625 с;

а частоты ₁ = 0.628 с^-1, ₂ = 1.05 с^-1, ₃ = 10 с^-1, ₄ = 100 с^-1, ₅ = 160 с^-1.

Далее строится желаемая ЛФЧХ и определяются запасы устойчивости скорректированной системы.