3.4. Параметрическая оптимизация систем наведения.

Постановка задачи заключается в следующем: требуется найти значения параметров k_i корректирующих устройств К_у1(р), К_у2(р), К_у3(р) (двух параметров при фиксированных остальных), обеспечивающих минимальную установившуюся ошибку системы  на входном сигнале вида (t) = a₀ + a_1t, причем область допустимых значений параметров ограничивается условием, чтобы время переходного процесса в системе не превышало заданной величины t_пп. Таким образом рассматривается задача на условный экстремум. В настоящей методике предлагается получить аналитическую зависимость установившейся ошибки  от параметров системы - k_i ,т.е. (k_i) и аналитическую зависимость времени переходного процесса t_п от этих же параметров, т.е. t_п(k_i). Тогда задача параметрической оптимизации может быть сформулирована следующим образом:

Требуется найти значения параметров k_i обеспечивающих

min (k_i) при уловии, что t_п(k_i)  t_пп .

Основная проблема заключается в определении аналитических зависимостей от параметров ошибки и времени переходного процесса.

Определение аналитической зависимости ошибки системы от параметров системы осуществляется следующим образом:

• составляется передаточная функция системы по ошибке - Ф_(р),

• полученная передаточная функция раскладывается в ряд по возрастающим степеням р,

(33)

• определяются коэффициенты ошибок системы - с_l(k_i) (l =0,1,2),

• по формуле установившейся ошибки

(34)

находится искомая зависимость.

Определение аналитической зависимости времени переходного процесса от параметров системы и построение области допустимых значений параметров осуществляется в следующей последовательности:

- строится характеристическое уравнение системы (р)=0,

- определяется значение вещественной части корней характеристического уравнения системы по формуле

. (35)

- задаемся значениями корней р= ,

• подставляем значения р в характеристический уравнение,

• методом D-разбиения получаем область параметров (в пространстве параметров) в которой обеспечивается заданное время переходного процесса.

Область дополнительно ограничивается условиями возможной реализации коэффициентов усиления k_i < 10000.

B полученной области методами линейного или нелинейного программирования определяются параметры, обеспечивающие минимальную ошибку.

Пример 5. Параметрическая оптимизации системы наведения.

Рассматривается система заданная следующей структурной схемой, рис.13.

Требуется определить параметры К₁,К₂ , обеспечивающие минимальную установившуюся ошибку, причем время переходного процесса t_п  t_пп =1 с.

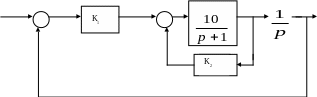
Рис.13.

Определение зависимости установившейся ошибки от параметров системы.

Передаточная функция разомкнутой системы

.

Параметры К_1, К₂ необходимо выбрать таким образом, чтобы они обеспечивали минимальную установившуюся ошибку при входном воздействии (t) = 0.05t, а время переходного процесса в системе не превышало бы 1 сек.

Передаточная функция замкнутой системы по ошибке имеет вид:

.

Полиномы числителя и знаменателя расписываются по возрастающим степеням р.

В этом случае передаточная функция легко разлагается в ряд по возрастающим степеням при р простым делением числителя на знаменатель. Обычно достаточно двух или трех членов разложения. Ниже приведена схема деления полиномов

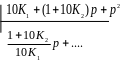
Окончательно имеем следующее разложение

т.е. коэффициенты ошибок следующие

Установившаяся ошибка определяется из формулы

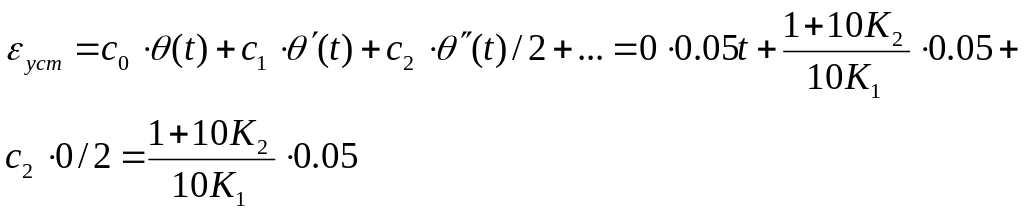(36)

т.е. целевая функция, связывающая параметры К₁ и К₂ - линейна, поскольку из (36) следует

. (37)

Определение области параметров (в пространстве параметров) в которой обеспечивается заданное время переходных процессов.

Время переходного процесса связано со значением вещественной части корней характеристического уравнения соотношением

.

Тогда для t_пп=1c, имеем

Характеристическое уравнение получим приравняв 0 знаменатель передаточной функции системы по ошибке

Подставив в него , получим

. (38)

Изменяя  от - до  и решая для каждого  это уравнение, получим на плоскости параметров К₁ и К₂ границы области в которой время переходных процессов не превышает 1 сек. Такой метод построения областей допустимых значений параметров получил название метода D-разбиений. Аналитическое построение границ области осуществляется следующим образом.

Приравнивая нулю вещественную и мнимую части уравнения (38), получим

(39)

Необходимо рассмотреть два случая:

1.  = 0. Тогда второе уравнение в (38) выполняется автоматически, а из первого следует уравнение первой границы (прямая 1 на рис.14)

.

2.   0. Тогда из второго уравнения следует 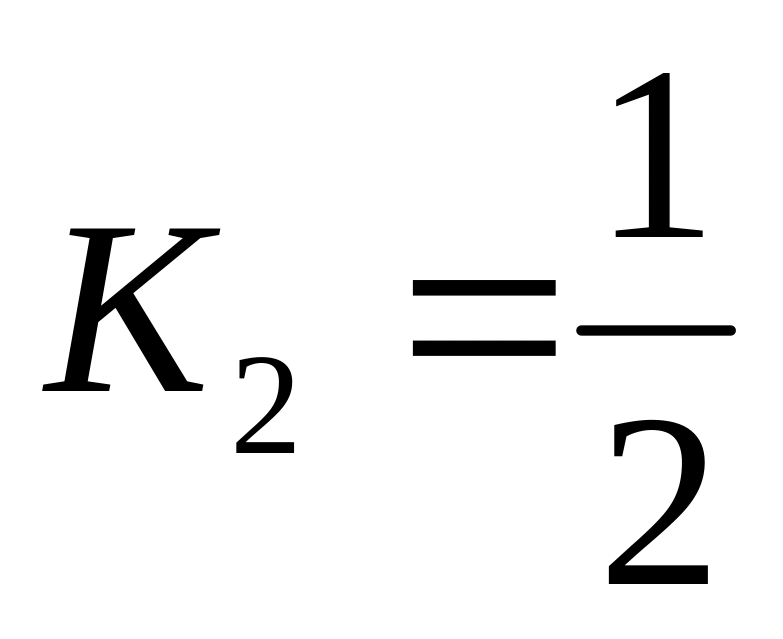. Подставив полученное значение К₂ в первое уравнение, получим

. Полученные два соотношения, с учетом изменения  от 0 до  , определяют вторую границу области (прямая 2 на рис.14).

Область допустимых значений параметров заключена между этими прямыми.

С учетом ограничений К₁,К₂  10000, получим замкнутую область (на рис.14 - заштрихованная область).

Определение оптимальных значений параметров осуществляется из следующих соображений. Поскольку область допустимых значений параметров ограничена прямыми, и сама целевая функция (37) линейна, то задача оптимизиции относится к задачам линейного программирования (в противном случае - нелинейного). Известно, что оптимальное решение, при условии выпуклости области допустимых значений параметров, лежит на границе этой области.

Дадим графическую интерпретацию решения задачи параметрической оптимизации, рис.14.

Зададим значение в (37), равным нулю, тогда целевая функция имеет вид

. Полученная прямая не касается заштрихованной области допустимых значений параметров и, следовательно решения в этом случае нет. Будем увеличивать . Очевидно, что при некотором , целевая функция каснется области в точке А. Значения параметров в этой точке - оптимальны, т.е.

Значение установившейся ошибки получается после подстановки полученных значений параметров в выражение ошибки (36).

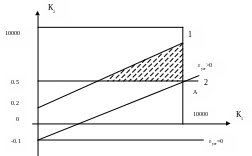
Рис.14.