1. Пояснительная записка. Целевая установка.

Данное пособие содержит учебно-методические рекомендации по изучению курса «Линейное программирование» для студентов экономического факультета по специальностям «Экономика и управление на предприятии», «Бухгалтерский учёт и аудит», «Прикладная информатика в экономике». Пособие содержит теоретический материал, иллюстрированный примерами решения основных задач с экономическим содержанием.

Целевая установка.

Цель пособия – оказать помощь студентам в изучении курса «Линейное программирование» для развития навыков по применению различных математических методов и моделей в решении задач торгово-коммерческой и управленческой экономической деятельности, а также подготовить студентов к самостоятельному изучению литературы по математическим методам в экономике.

В результате изучения дисциплины каждый студент должен

знать: возможности экономико-математического аппарата и принципы его использования при самостоятельной постановке простейших экономических задач;

уметь: формализовать и решать экономические задачи с использованием экономико-математического аппарата.

2. Программа:

   1. Моделирование экономических процессов коммерческого предприятия.

   2. Решение задачи ЛП на основе её геометрической интерпретации.

   3. Решение моделей симплексным методом.

   4. Двойственная задача к задаче планирования работы коммерческого предприятия.

   5. Транспортная задача. Построение первого опорного плана. Нахождение оптимального плана.

3. Рекомендуемая литература.

   1. Ляшенко И.Н. «Линейное и нелинейное программирование», - Киев: «Вища школа», 1975.

   2. Кузнецов Ю.Н. «Математическое программирование», - М: «Высшая школа», 1976.

   3. Лунгу К.Н. «Линейное программирование (руководство к решению задач)», - М: «Физматлит», 2005.

   4. Плотников А.Д. «Математическое программирование», - Минск: «Новое знание», 2006.

   5. Красс М.С., Чупырнов Б.П. «Математика для экономистов», - С-Пб: «Питер», 2007.

   6. Палий И.А. «Линейное программирование», - М: «Эксмо», 2008.

4. Методические указания. Тема 1. Общее линейное программирование (лп).

1. Основные понятия и определения.

Определение. Линейное программирование – это область математического программирования (т.е. поиск некоторой программы действий), являющаяся разделом математики, в котором изучаются методы исследования и отыскания экстремальных (наибольших и наименьших) значений некоторой линейной функции, на аргументы которой наложены линейные ограничения.

Такая линейная функция называется целевой, а набор количественных соотношений между переменными, выражающих определённые требования экономической задачи в виде уравнений или неравенств, называется системой ограничений.

Определение. Совокупность соотношений, содержащих целевую функцию и ограничения на её аргументы, называется математической моделью экономической задачи оптимизации.

В общем виде математическая модель задачи линейного программирования записывается как

при условиях-ограничениях

a_ij, b_i, c_j – заданные постоянные величины.

Определение. Стандартной (или симметрической) задачей ЛП называется задача, имеющая вид

или

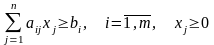
Определение. Канонической (или основной) задачей ЛП называется задача, имеющая вид

Стандартную задачу можно привести к каноническому виду, вводя дополнительные (или вспомогательные) переменные в левые части неравенств.

Определение. Совокупность чисел при котором целевая функция принимает максимальное (минимальное) значение называется оптимальным решением задачи ЛП.

Всякая же другая совокупность значений, удовлетворяющая ограничениям определяет допустимое решение (план).