Тема: Решение позиционных задач по теме «Точка и прямая в ортогональных проекциях».
Цель занятий: изучить методы проецирования точки, прямой; научится находить следы прямой, решать позиционные задачи по данной теме.
Задание: Изучить краткие теоретические сведения и решить
задачи.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Позиционными задачами называются задачи, связанные с определением на комплексном чертеже взаимного расположения заданных геометрических фигур, включая задачи на взаимную принадлежность и на взаимное пересечение. 1 группа задач 1. Принадлежность точки прямой (свойство параллельного проецирования). 2. Принадлежность точки плоскости (строится линия,∈ плоскости). 3. Принадлежность точки поверхности (строится линия, ∈ поверхности). 2 группа задач Принадлежность линии плоскости и поверхности. 3 группа задач Принадлежность плоскости поверхности (невозможно в общем случае - исключение гранная поверхность, но тогда происходит совпадение плоскостей). В общем случае возможно только касание - предельное положение пересечения.
Точка в ортогональной системе двух плоскостей проекций. |
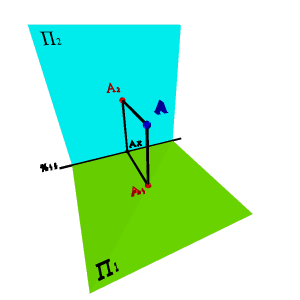
При построении проекции необходимо помнить, что ортогональной проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на эту плоскость. На рисунке 1.1. показана точка А и ее ортогональные проекции А1 и А 2.
Точку А1 называют горизонтальной проекцией точки А, точка А2 - ее фронтальной проекцией. Проекции точки всегда расположены на прямых, перпендикулярных оси x21 и пересекающих эту ось в одной и той же точке А x.
|
|
|
а) модель |
|
б) эпюр |
Рисунок. 1.1. Точка в системе двух плоскостей проекций
|
||
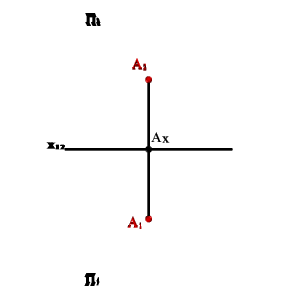
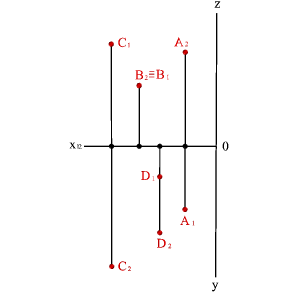
Справедливо и обратное, т. е. Если на плоскостях проекций даны точки А1 и А2 расположенные на прямых, пересекающих ось x21 в точке Аx под прямым углом, то они являются проекцией некоторой точки А.
На эпюре Монжа проекции А1 и А2 окажутся расположенными на одном перпендикуляре к оси x21. При этом расстояние А1Аx -от горизонтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П2, а расстояние А2Аx - от фронтальной проекции точки до оси равно расстоянию от самой точки А до плоскости П1.
Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.
|
|
|
а) модель |
|
б) эпюр |
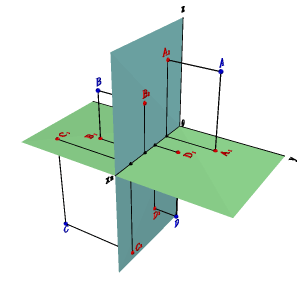
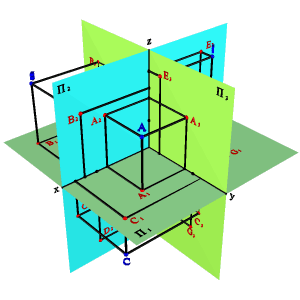
В практике изображения различных геометрических объектов, чтобы сделать проекционный чертеж более ясным, возникает необходимость использовать третью – профильную плоскость проекций П3, расположенную перпендикулярно к П1 и П2. В соответствии с ГОСТ 2.305-68 плоскости проекций П1 П2 и П3 относятся к основным плоскостям проекций.
Модель трех плоскостей проекций показана на рисунке 1.2. Третья плоскость, перпендикулярная и П1, и П2, обозначается буквой П3 и называется профильной.
Если точка принадлежит хотя бы одной плоскости проекций, она занимает частное положение относительно плоскостей проекций. Если точка не принадлежит ни одной из плоскостей проекций, она занимает общее положение.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Способы графического задания прямой линии
1.Двумя точками ( а и в ).
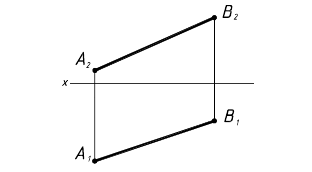
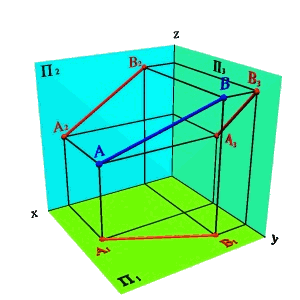
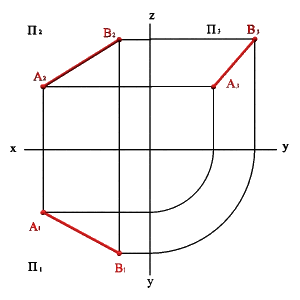
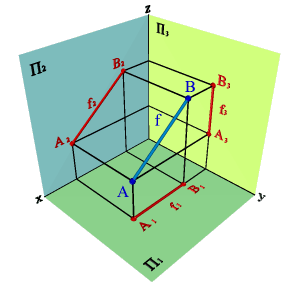
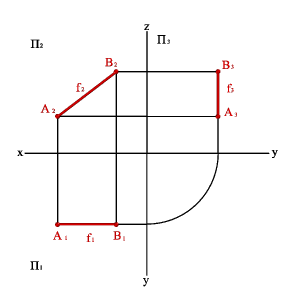
Рассмотрим две точки в пространстве А и В (рис. 2.1). Через эти точки можно провести прямую линию получим отрезок [BA]. Для того чтобы найти проекции этого отрезка на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка:
[A1B1]<[BA]; [A2B2]<[BA;] [A3B3]<[BA].
|
|
|
а) модель |
|
б) эпюр |
Рисунок 2.1.Определение положения прямой по двум точкам
|
||
Обозначим углы между прямой и плоскостями проекций через a- с плоскостью П1, b- с плоскостью П2, g- с плоскостью П3 и тогда получим:
½А1В1½=½BA½cos a
½A2B2½=½AB½cos b
½A3B3½=½AB½cos g.
Частный случай ½A1B1½=½A2B2½=½A3B3½ при таком соотношении прямая образует с плоскостями проекций равные между собой углы »g=b=a350, при этом каждая из проекций расположена под углом 450 к соответствующим осям проекций.
2. Двумя плоскостями (;a )b.
Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
3. Двумя проекциями.
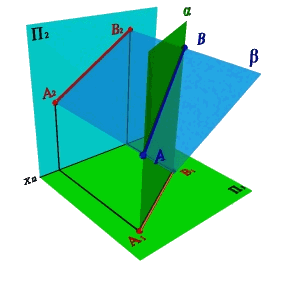
Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [А1В1] и [A2B2]. Проведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис.2.2а), линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А1В1] и [А2В2].
|
|
|||
|
а) |
|
|
б) |
Рисунок 2.2.Определение положения прямой в пространстве по двум проекциям отрезка |
||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
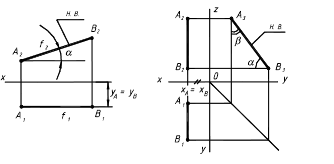
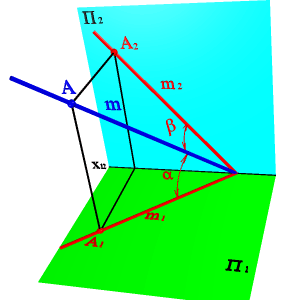
Рисунок 2.3.Определение положения прямой по точке и углам наклона к плоскостям проекций
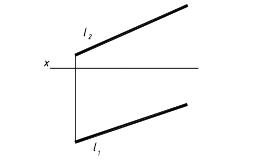
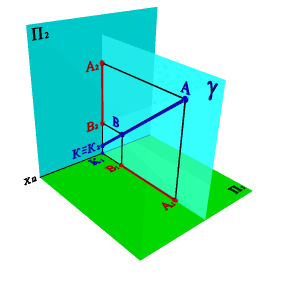
Плоскости a и b могут слиться в одну плоскость g, если, например, проекции [А1В1] и [А2В2] перпендикулярны оси x и пересекают ее в одной точке (рис.2.2.б). Прямая линия в этом случае будет однозначно определена своими проекциями, если на каждой из них обозначить две какие-либо точки. Если же обозначений не делать, то за искомую прямую можно принять любую прямую, лежащую в этой плоскости при условии, что она непараллельная ни одной из плоскостей проекций. Точка К, в данном случае - точка пересечения прямой с плоскостью П2. 4. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве (рис.2.3).
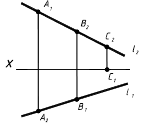
Положение прямой относительно плоскостей проекций. Следы прямой. В зависимости от положения прямой по отношению к плоскостям проекций она может занимать как общее, так и частные положения. 1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.2.4).
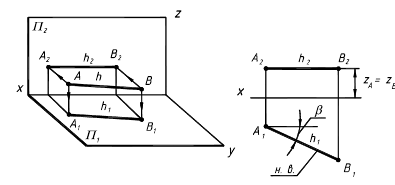
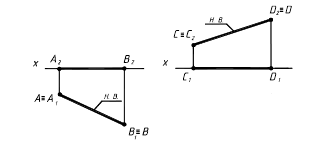
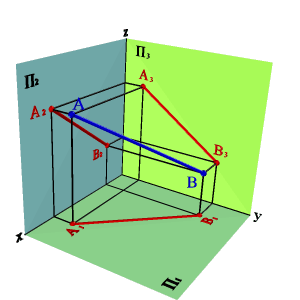
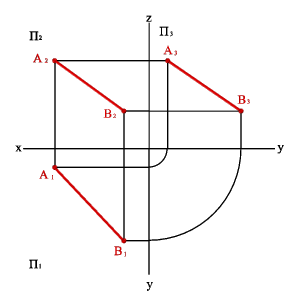
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают: 2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.2.5). Для любой пары точек горизонтали должно быть справедливо равенство zA=zB Þ A2B2//0x; A3B3//0y Þ xAx–B,0# yAy–B,0# zAz–B.0=
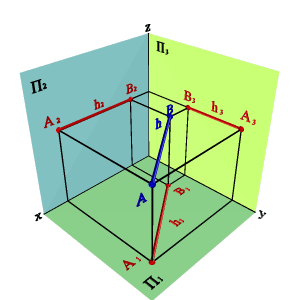
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями (рис.2.6). yAy=BÞ A1B1//,x0 A3B3//z0 Þ xAx–B,0# yAy–B,0= zAz–B.0#
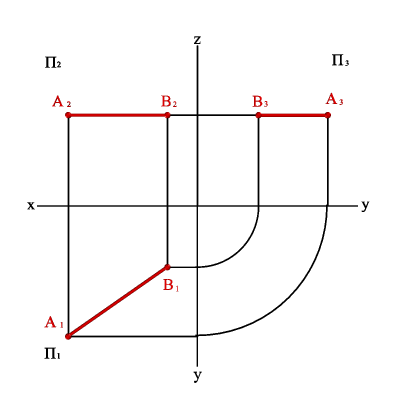
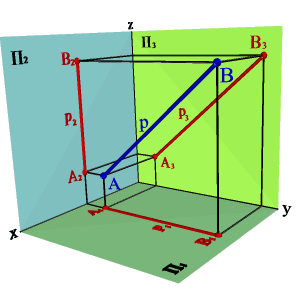
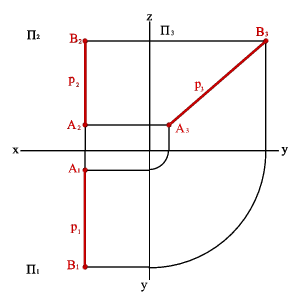
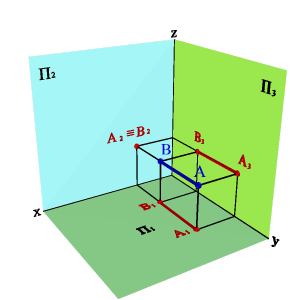
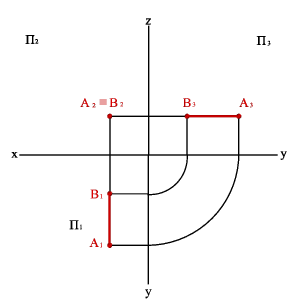
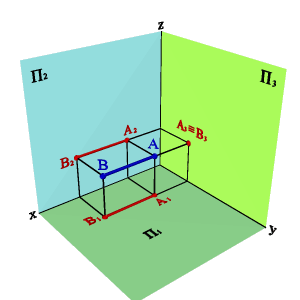
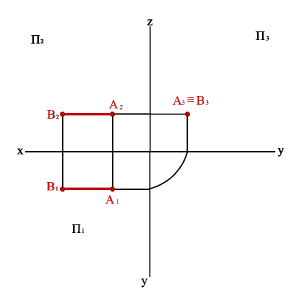
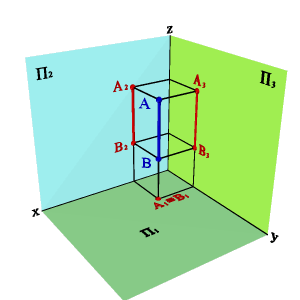
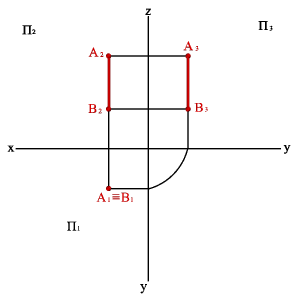
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 2.7). xA=xBÞ A1B1//0,y A2B2//z0 Þ xAx–B,0= yAy–B,0# zAz–B.0# Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.
3. Прямые перпендикулярные плоскостям проекций, называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают: 3.1. Фронтально проецирующая прямая - АВ .Рсир( 2.8.) xAx–B0=ü yAy–B0#ý zAz–B=0þ,
3.2. Профильно проецирующая прямая - АВ (рис.2.9) xАx–B0#ü yАy–B0=ý zАz–B0=þ,
3.3. Горизонтально проецирующая прямая - АВ (рис.2.10) xАx–В0=ü yАy–В0=ý zАz–В0#þ.
Следы прямой линии
а
б Рис. 2.1. Изображение следов прямой линии: а – в пространстве; б – на эпюре Следом прямой линии называется точка пересечения прямой с плоскостью проекций. В системе двух плоскостей проекций π1 и π2 прямая в общем случае имеет два следа:
Это точки пересечения прямой соответственно с горизонтальной и фронтальной плоскостями проекций. Установим правило нахождения следов прямой. Для нахождения горизонтального следа прямой необходимо: 1) продолжить фронтальную проекцию прямой а до пересечения с осью Х (получим точку НХ ≡ Н2) 2) восстановить перпендикуляр в точке НХ к оси Х (провести линию связи перпендикулярную к оси Х); 3) продолжить горизонтальную проекцию прямой а до пересечения с перпендикуляром; 4) полученная точка пересечения и будет являться горизонтальным следом прямой а Н ≡ Н1 Для нахождения фронтального следа прямой необходимо: 1) продолжить горизонтальную проекцию прямой а до пересечения с осью Х (точка FX ≡ F1); 2) восстановить перпендикуляр в точке FX к оси Х; 3) продолжить фронтальную проекцию прямой до пересечения с перпендикуляром; 4) полученная точка пересечения F ≡ F2 является фронтальным следом прямой а В начертательной геометрии считается, что наблюдатель расположен в первом пространственном углу на бесконечном расстоянии от плоскостей проекций, поэтому видимыми геометрическими фигурами будут только те, которые расположены в первом октанте. Проекции этих фигур в ортогональных и аксонометрических проекциях показываются сплошными линиями. Фигуры, расположенные в других пространственных углах, не видны наблюдателю, и их проекции показываются штриховыми линиями.
1.Прямая 1.1. Проекции прямой Прямая линия – это совокупность последовательных положений точки, движущейся в пространстве. При ортогональном проецировании (в общем случае) согласно свойствам параллельного проецирования прямая проецируется в прямую. Для построения проекций прямой достаточно построить проекции двух нетождественных точек, принадлежащих данной прямой.
Рис. 2.1 Прямую на эпюре можно задавать не только проекциями ее отрезка, но и проекциями некоторой произвольной части прямой. При этом проекцию обозначают одной буквой.
Рис. 2.2 1.2. Классификация прямых По своему положению относительно плоскостей проекций прямые подразделяются на: прямые общего положения частного положения
прямые не | | и не ⊥ уровня проецирующие ни к одной из плоскостей проекций Прямые общего положения проецируются на плоскости проекций с искажением, причем проекции отрезка всегда меньше самого отрезка (рис. 2.1, рис. 2.2). Прямые уровня – это прямые | | одной из плоскостей проекций. Они подразделяются на прямые:
1. Горизонтального 2. Фронтального 3 Профильного. уровня уровня уровня АВ | | П1 АВ | | П2 АВ | l П3 ZA=ZB, ∧ A2B2 | | x, β = AB П2
Рис. 2.3
yA= yB ∧ x A = x B A1B1| | x α = AB П1 A 2 B 2 | | z , A 1 B 1 | | y Рис. 2.4 Прямые ∈ одной из плоскостей проекций называются рамными нулевого уровня.
АВ∈ П1 CD∈ П2
Рис. 2.5 Проецирующие прямые – это прямые ⊥ к одной из плоскостей проекций (и | | двум другим плоскостям проекций). Проецирующие прямые
1.3. Точка на прямой Аксиома (принадлежности). Если точка принадлежит прямой, то одноименные проекции точки принадлежат одноименным проекциям прямой. Пример. Определить, какие из заданных точек ∈ прямой L.
B ∈ l, т. к. B1∈ l1, B2 ∈ l2
Рис. 2.7
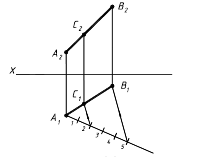
1.4. Деление отрезка в данном отношении Теорема. Если точка делит отрезок прямой в данном отношении, то проекции этой точки делят проекции данной прямой в том же отношении. Пример. Разделить отрезок АВ точкой С в отношении 2:3, считая от точки А.
АС : СВ=2:3
Рис. 2.8 Из горизонтальной проекции точки А проводим вспомогательную прямую и откладываем на ней 5(2+3) отрезков произвольной длины, но равных между собой. Проводим отрезок 5В1 и | | ему через точку 2 проводим прямую до пересечения с горизонтальной проекцией прямой А1В1. Получаем проекцию точки С1 и затем точку С2 , таким образом точка С делит отрезок АВ в отношении 2:3. Для профильных прямых необходимо проверка по третьей проекции.
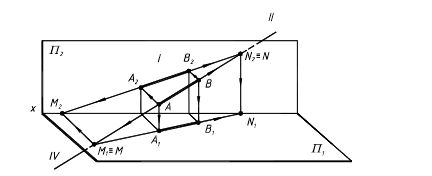
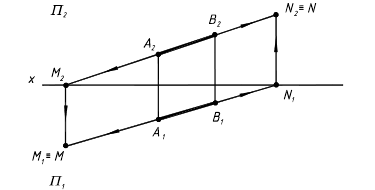
1.5. Следы прямой Следом прямой называется точка пересечения прямой с плоскостью проекций. Прямая общего положения в системе трех плоскостей проекций имеет три следа: горизонтальный, фронтальный и профильный. Прямая не имеет следа на плоскости проекций, если она | | этой плоскости проекций. Для построения горизонтального следа прямой необходимо продолжить прямую до пересечения с горизонтальной плоскостью проекций П1 , при этом горизонтальная проекция горизонтального следа М1 совпадает с самим следом М, а фронтальная проекция горизонтального следа М2 лежит на оси проекций х. Аналогично, для построения фронтального следа N необходимо продолжить прямую до пересечения с фронтальной плоскостью проекций, при этом фронтальная проекция N2 фронтального следа N совпадает с самим следом, а горизонтальная проекция фронтального следа N1 лежит на оси проекций.
Рис. 2.9 Правило. Чтобы построить горизонтальный след прямой М, необходимо фронтальную проекцию прямой продолжить до пересечения с осью х и получить фронтальную проекцию горизонтального следа М2. Из полученной точки восстановить или опустить ⊥ до пересечения с продолжением горизонтальной проекции прямой. Получаем горизонтальный след М, совпадающий с ее горизонтальной проекцией М1.
Рис. 2.10
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
.
