Лекции / Лекция по основам искусственного интеллекта №5

Лекция № 5

Распознавание образов с помощью нейронных сетей

1. Описание задачи и практические приложения задачи распознавания образов.

Многие существующие задачи можно интерпретировать как задачи распознавания (классификации). Например, имеется немало вариантов изображения цифры 1, но все эти изображения должны принадлежать к одному классу – классу «1»; распознавание слов в звуковой записи, воспроизводимой динамиком магнитофона – тоже пример распознавания (классификации).

Когда мы знаем, к какому классу относится каждый из учебных примеров, можно использовать управляемое обучение. Задачей для сети является ее обучение тому, как сопоставить предъявляемый образец с контрольным целевым образцом, представляющим нужный класс. Например, сети можно предъявить изображений цифры 1 и обучить сеть тому, что при этом соответствующий 1 выходной элемент должен быть включен. А выходные элементы, соответствующие другим цифрам - выключены. В этом случае входной образец может быть набором значений. Характеризующих пиксели изображения в оттенках серого, а целевой выходной образец – вектором, значения всех координат которого должны быть равными 0, за исключением координаты, соответствующей выходному элементу, представляющему 1.

Чтобы понять каким образом работает НС при решении задачи распознавания, рассмотрим тривиальную задачу и используем для решения этой задачи самый простой тип сети.

Задача состоит в выработке правил классификации самолетов для бомбардировщиков и истребителей в зависимости от их максимальной скорости и максимального взлетного веса (рис. 1). Такие правила могут быть заданы формально:

ЕСЛИ вес>0.80 И скорость < 0.55, ТО бомбардировщик,

ЕСЛИ вес<0.90 И скорость > 0.25, ТО истребитель,

Разделение, порожденное этими правилами, вполне успешно классифицирует самолеты, но оказывается не слишком гибким, если по этим правилам придется классифицировать новый самолет.

Рис. 1.

Кроме того, эти правила в указанном виде ничего не сообщают о том, насколько точной будет классификация нового самолета.

Альтернативный подход к использованию правил заключается в выводе функции классификации путем построения прямой, разделяющей два класса. Для нового самолета нам нужно просто указать точку на плоскости, соответствующую известным значениям максимальной скорости и максимального взлета и посмотреть, по какую сторону от прямой будет расположена эта точка. В данном случае для небольшого числа самолетов рассмотрены два признака, скорость и вес, поэтому можно представить данные в виде изображения на плоскости. Однако если придется иметь дело с сотнями самолетов и значительно большим числом признаков, задачу классификации в виде простой картинки представить будет невозможно.

Выход заключается в использовании функции выбора решения. Уравнение прямой, разделяющей два типа самолетов, записывается в следующем виде:

х₂=1.5х₁+0.5

где х₁ представляет скорость, а х₂ – вес. Это уравнение можно использовать для создания функции выбора решения:

Например, истребитель, представленный точкой (0.4, 0.5), даст

и функция выбора решения правильно классифицирует эту точку, как истребитель.

Предлагаемую функцию выбора решения можно моделировать с помощью нейронной сети и реализовать в виде аппаратных средств

2. Проблема разделения классов (проблема «исключающего ИЛИ»)

Для задачи классификации, например, выяснения типа самолетов, если прямая (для размерности два) или гиперплоскость (для размерности n) может разделить все образцы на соответствующие им классы, то проблема является линейной. Если же для решения проблемы разделения классов требуется несколько прямых или гиперплоскостей, то проблема называется нелинейной. Широко известным примером нелинейной проблемы является проблема моделирования отношения XOR. Определение отношения XOR приведено в таблице 1.

Таблица 1.

х	у	z
1	1	0
1	0	1
0	1	1
0	0	0

Проблема XOR таким образом является нелинейной, и для ее решения с помощью НС имеется две возможности: либо использовать сеть, которая будет строить две или больше прямых для разделения данных, либо изменить вид вводимых данных. Последняя возможность может превратить проблему в линейную, если к двум имеющимся вводимым признакам добавить третий и сделать пространство вводимых данных трехмерным (в результате два класса будут размещаться в двух противоположных вершинах куба). Однако данный подход не является нейронным решением, поэтому предпочтительным является работа сети в условиях нелинейной проблемы. Таким образом, мы сосредоточимся на решении, использующем две прямые для разделения классов. Такая сеть потребует элемента, каждый из которых получит на входе по два значения, чтобы представить две разделяющие прямые, и третий элемент, объединяющий информацию об этих двух прямых. Проблема моделирования отношения XOR приведена на рис. 2.

Рис. 2.

На рис. 3. приведена архитектура НС, которая будет моделировать две разделяющие границы.

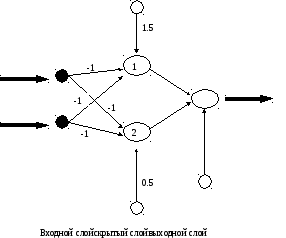
Рис. 3.

Для элементов входного слоя будут использоваться индекс i , для элементов скрытого слоя – j, а для элементов выходного слоя – k. В сети на рис. 3. элементы разделены на три слоя. Элементы первого слоя являются элементами ввода данных в сеть. Второй слой элементов называется скрытым слоем – скрытые элементы связаны только с другими элементами и не имеют непосредственных связей с внешней средой. Выходной слой предназначен для передачи ответа сети во внешнюю среду.

В табл. 2. показаны комбинированный ввод и вывод (при использовании пороговой функции) для элементов скрытого слоя при ответе на вводимые данные проблемы XOR.

Таблица 2.

		Комбинированный ввод скрытого слоя		Вывод скрытого слоя
х	у	Элемент 1	Элемент 2	Элемент 1	Элемент 2
1	1	-0.5	-1.5	0	0
1	0	0.5	-0.5	1	0
0	1	0.53	-0.5	1	0
0	0	1.5	0.5	1	1

Вводимые образы преобразуются под воздействием весовых коэффициентов первого слоя и скрытых элементов. Второй слой весов, соединяющих скрытый слой с выходным слоем, тоже будет моделировать прямую, поскольку у единственного выходного элемента также имеется два вводимых значения и значение смещения. Если выходной элемент правильно указывает класс, соответствующий каждому вводимому образцу, то данные ввода для второго слоя весов должны быть линейно отделимы. Можно проверит это с помощью нанесения на плоскость точек, соответствующих выводу скрытых элементов, как показано на рис. 4.

(1,1)

(0,1)

(1,0)

Рис. 4.

Как видно из рис. 4. в результате прохождения первого слоя весов исходная точка (0,1) переместилась в (1,0), а точки (0,0) и (1,1) поменялись местами.

Прежде чем обратиться к рассмотрению алгоритма обучения, дающего возможность сети научиться находить решения, необходимо подчеркнуть важность функции преобразования (функции активности), связываемой с каждым элементом сети. Примером нелинейной функции активности является пороговая функция. Примером линейной функции является тождественная функция, при которой вывод оказывается равным вводу.

3. Обучение по алгоритму обратного распространения ошибки

В общем случае задача обучения НС сводится к нахождению некой функциональной зависимости Y=F(X) где X– входной, а Y– выходной векторы. В общем случае такая задача, при ограниченном наборе входных данных, имеет бесконечное множество решений. Для ограничения пространства поиска при обучении ставится задача минимизации целевой функции ошибки НС, которая находится по методу наименьших квадратов:

(1)

где

y_j– значение j-го выхода НС

d_j– целевое значение j-го выхода

p– число нейронов в выходном слое

Обучение НС производится методом градиентного спуска, т.е. на каждой итерации изменение веса производится по формуле

(2)

где h – параметр, определяющий скорость обучения.

(3)

где

y_j – значение выхода j-го нейрона

S_j – взвешенная сумма входных сигналов, определяемая по формуле

При этом множитель

(4)

где

– значение i-го входа нейрона

Далее рассмотрим определение первого множителя формулы (3)

(5)

где

k – число нейронов в слое n+1.

Введем вспомогательную переменную

(6)

Тогда мы сможем определить рекурсивную формулу для определения n-ного слоя, если нам известно следующего (n+1)-го слоя.

(7)

Нахождение же для последнего слоя НС не представляет трудности, так как нам известен целевой вектор, т.е. вектор тех значений, которые должна выдавать НС при данном наборе входных значений.

(8)

И наконец запишем формулу (6) в раскрытом виде

(9)

Рассмотрим теперь полный алгоритм обучения НС:

1. подать на вход НС один из требуемых образов и определить значения выходов нейронов НС

2. рассчитать 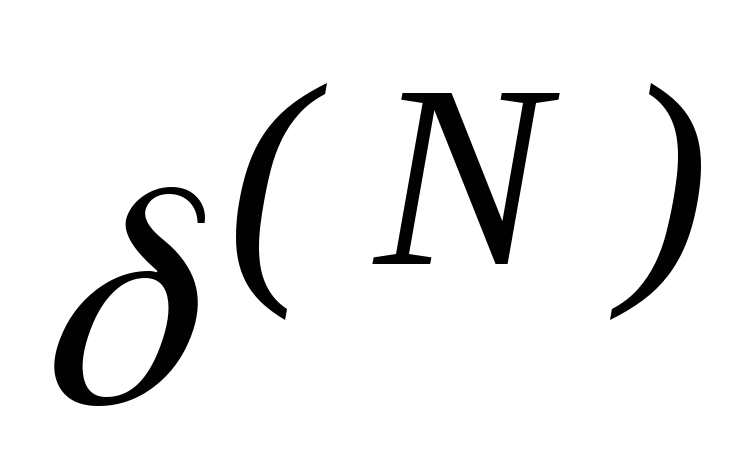для выходного слоя НС по формуле (8) и рассчитать изменения весов выходного слоя N по формуле (9)

3. Рассчитать по формулам (7) и (9) соответственно 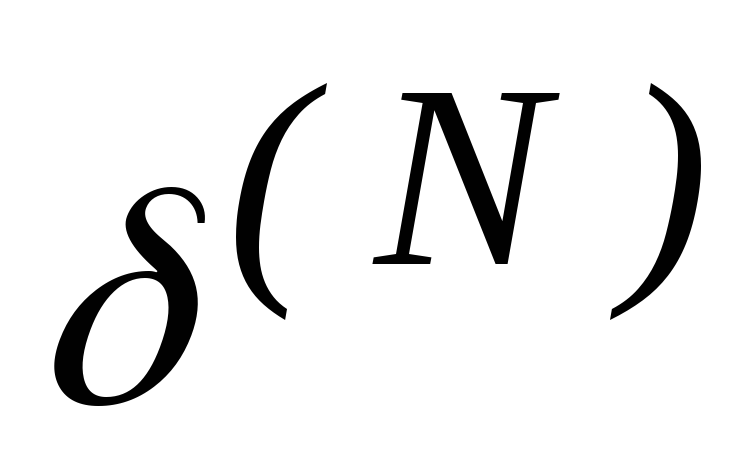и 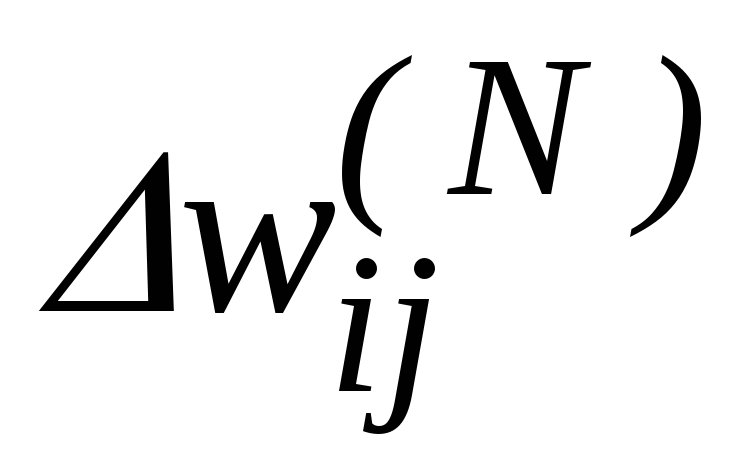для остальных слоев НС,

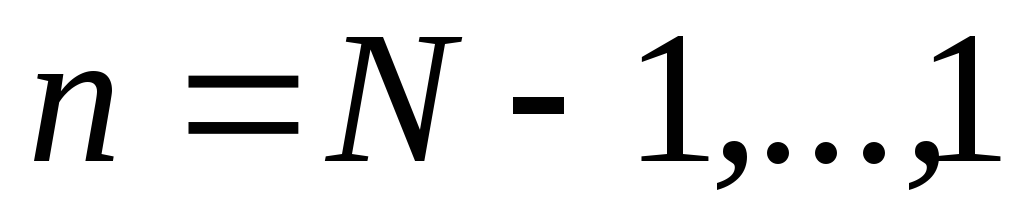
4. Скорректировать все веса НС

(10)

5. Если ошибка существенна, то перейти на шаг 1

На этапе 2 сети поочередно в случайном порядке предъявляются вектора из обучающей последовательности.