Результаты определения характеристик группировочного признака отразим в таблице 2: «Расчет характеристик интервального ряда распределения».

Таблица 2 - Расчёт характеристик интервального ряда распределения

№ Группы	Интервал по груп. признаку	Частота		Частость W, %	Величина интервала, h	Центр интервала, хср	Плотность распределения
		f	S				Абсолютная, ρа	Относительная, ρо
гI	230-268	1	11	5	38	249	0,03	0,1
I II	269-307	4	55	20	38	288	0,1	0,5
IIII	308-346	2	77	10	38	327	0,05	0,3
IIV	347-385	6	113	30	38	367	0,2	0,8
VV	386-424	7	220	35	38	405	0,2	0,9
	Итого	220	хХ	100	Х	325	Х	Х

8. Графическое изображение интервальных рядов распределения путем построения гистограммы, полигона распределения (Приложение 5) и кумулятивной кривой (Приложение 6).

Гистограмма – график, на котором ряд распределения изображен в виде смежных друг с другом столбиков. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенных на соответствующих интервалах.

Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот.

При помощи кумуляты изображается ряд накопленных частот. При построении кумуляты по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.

Далее отражаем показатели в таблице, которые характеризуют группы, и определяем их средние характеристики для каждой группы. Данная таблица строится на основе вспомогательных таблиц (Приложение 7, Приложение 8).

Таблица 3 - Зависимость себестоимости картофеля от факторов интенсификации

Группы по себестоимости 1ц картофеля, руб.	Число предприятий	В среднем по группе на 1 га						Средняя себестоимость 1 ц, руб.
		Урожайность, ц	Общие затраты производства, тыс.руб.	Материальные затраты, тыс.руб.	Затраты на оплату труда, тыс. руб.	Затраты на содержание основных средств, тыс.руб.	Прочие затраты, тыс.руб.
1	2	3	4	5	6	7	8		9
1(230-268)	1	136	31,28	12,21	7,82	7,19	4,07		230
2(269-307)	4	104	29,33	10,99	6,02	7,64	4,68		282
3(308-346)	2	105	37,05	12,45	9,01	8,44	7,15		353,6
4(347-385)	6	105	38,02	19,02	9,98	5,71	3,31		362
5(386-424)	7	101	41,40	7,84	10,96	10,96	4,19		408
В среднем по совокупности	20	104,22	36,64	16,07	9,14	7,21	4,22		352

Проанализируем показатели таблицы, то есть проследим зависимость себестоимости овощей от урожайности и уровне эффективности в совокупности предприятий. В таблице прослеживается увеличение средней себестоимости от первой до пятой группы (230 до 408,096).

Во всех остальных показателях: урожайность; общие затраты; затраты на оплату труда; материальные затраты; затраты на содержание основных средств; прочие затраты себестоимость однородна.

Рассмотрим данные таблицы 3 и отберем факторы по которым построим два интервальных ряда распределения, то есть Огивы-Гальтона (Приложения 9-14) и на этой основе выполняем комбинационную группировку с включением себестоимости. В данной курсовой работе комбинационная группировка строится по двум признакам: урожайность и материальные затраты на 1га картофеля, т.к. у этих факторов наиболее четко проявляется зависимость с результативным показателем – себестоимостью (таблица 5).

Таблица 5 - Зависимость себестоимости картофеля от урожайности и материальных затрат на 1га посадок картофеля

Группы по урожайности, ц/га	Подгруппы по материальным затратам, тыс.руб				В среднем по группе
	I.(9,04-12,43)	II.(12,44-15,83)	III.(15,84-19,23)	IV.(19,24-22,63)
I.(90-101,75)	280	390	396	397	295
II.(101,76-113,51)	294	410	375	382	339
III.(113,52-137,03)	230	280	-	-	253
В среднем по подгруппе	288	377	383	353	352

Данную таблицу можно рассчитать на основе вспомогательных таблиц (Приложение 15, Приложение 16).

Вывод: На основании рассчитанной таблицы можно сделать вывод , что при фиксированном значении материальных затрат и увеличении урожайности себестоимость зерна падает (с 410 до 280) та же закономерность прослеживается и в целом по подгруппам, т.е. наблюдается обратная закономерность. При фиксированном уровне урожайности (90-102) и увеличении материальных затрат себестоимость картофеля тоже увеличивается (280-397). Та же закономерность прослеживается и в целом по подгруппам.

Значит, под влиянием двух признаков на себестоимость картофеля, она будет уменьшаться: за счет снижения материальных затрат, при условии, что урожайность одинакова, и за счет увеличения урожайности при при пониженном уровне материальных затрат.

3.2 Определение средней себестоимости и изменение величины колеблемости признака

Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы.

Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.

На этапе статистической обработки могут быть поставлены самые различные задачи исследования, для решения которых нужно выбрать соответствующую среднюю. При этом необходимо руководствоваться следующим правилом: величины, которые представляют собой числитель и знаменатель средней, должны быть логически связаны между собой.

Используются две категории средних величин:

степенные средние;

структурные средние.

Первая категория степенных средних включает: среднюю арифметическую, среднюю гармоническую, среднюю квадратическую и среднюю геометрическую.

Вторая категория (структурные средние) - это мода и медиана.

Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по несгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.

Формула средней арифметической (простой) имеет вид

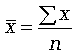
где n - численность совокупности.

Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.

Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:

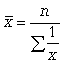
Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.

Для простой средней геометрической

Для взвешенной средней геометрической

Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения).

Формула простой средней квадратической

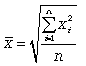
Формула взвешенной средней квадратической

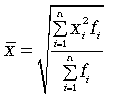
Средняя, рассчитанная по совокупности в целом, называется общей средней, средние, исчисленные для каждой группы, - групповыми средними. Общая средняя отражает общие черты изучаемого явления, групповая средняя дает характеристику размера явления, складывающуюся в конкретных условиях данной группы.

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.[3]

В процессе группировки решается задача – объединить в одну группу однородные по тому или иному признаку единицы, судить об однородности выделенных групп позволяет система показателей вариации. Методика расчета средних и показателей вариации признаков заключается в следующем:

1. Следует рассчитать среднее значение себестоимости картофеля в разрезе выделенных групп и в целом по совокупности (Приложения 19-23), обращая внимание на различие средних по группам по совокупности. В данном случае необходимо применять среднюю арифметическую взвешенную:

,

где х_i – отдельные значения себестоимости в определенном предприятии (руб),

f_i – валовой сбор (ц).

2. Рассчитать дисперсию, среднее квадратическое отклонение и коэффициент вариации себестоимости овощей в разрезе выделенных групп по себестоимости и в целом по совокупности.

Дисперсия есть не что иное, как средний квадрат отклонений индивидуальных значений признака от его средней величины. Дисперсия определяется по формуле:

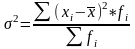
Среднее квадратическое отклонение:

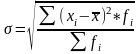
Данная величина (σ) имеет размерность и является обобщающей характеристикой абсолютных размеров вариации признака в совокупности. При расчете σ для себестоимости продукции она определяется в рублях.

Чтобы ответить на вопрос о мире вариации разных признаков одной и той же совокупности следует рассчитать коэффициент вариации:

Эта величина является относительной, что очень удобно для вариации в любых совокупностях. Чем больше величина V, тем больше разброс значений признака (х_i) вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.

3. Результаты расчетов покажем в таблице 5. Анализ данных этой таблицы позволяет судить об однородности совокупности в разрезе групп (т.к. коэффициент вариации в них не превышает 33%), устойчивости индивидуальных значений признака, а следовательно типичности средней. В то время как вся совокупность как по себестоимости, так и по урожайности и материальным затратам является неоднородной, то достижение однородности внутри групп подтверждает, что цель проведения группировки достигнута.

Таблица 6 - Анализ вариации себестоимости 1ц картофеля, урожайности и материальных затрат с 1га.

Группы	Себестоимость 1 ц.				Урожайность, 1 ц.				Мат. Затраты
	х,руб.	d,руб	d2	v,%	х,руб	d,руб	d2	v,%		х,руб	d,руб.	d2	v,%
1	230,00	0	0	0	95,5	2,85	8,1162	3,0		11,07	1,34	1,8282	1,97
2	282,00	5,77	33,35	2,05	106,9	2,93	8,5769	2,7		14,48	0,77	0,6127	1,36
3	353,70	10,1	101,33	3,04	136,5	2,51	6,3333	1,8		16,75	1,04	1,0593	1,24
4	362,30	12	144,29	3,2	-	0,00	0,0000	0,00		21,26	1,18	1,3759	1,12
5	408,10	12,1	147,44	2,99	-	0,00	0,0000	0,00		-	0,00	0,0000	0,00
В целом по совокупности	352,10	11,1	123,03	3,15	104,2	2,88	8,2861	2,7		15,7	1,18	1,3557	7,52

Вывод: Анализируя таблицы «Расчеты показателей вариации по урожайности, материальным затратам и себестоимости 1ц картофеля в разрезе выделенных групп» и «По совокупности в целом по себестоимости 1ц картофеля, по урожайности и материальным затратам с 1 га», можно сказать, что отклонение индивидуальных значений от средних по группам находятся в пределах 33%. Составляют: в первой группе- 0,00; во второй- 2,05; в третей – 3,04; в четвертой - 3,29; в пятой – 2,99. В целом по совокупности 3,15 – совокупность однородна.

Показатели вариации по материальным затратам находятся в пределах 33%. Составляют: в первой группе – 1,97; во второй – 1,36; в третьей – 1,24; в четвертой – 1,12; в пятой – 0,00. В целом по совокупности 7,52 – совокупность однородна.

По урожайности зерна в разрезе выделенных групп, можно сказать, что отношения индивидуальных значений урожайности от средних находятся в пределе 33%, следовательно, группы однородны, а средняя урожайность в них достоверна.