Оператори кросинговеру

Оператор схрещування безперервного ГА, або кросовер, породжує одного або декількох нащадків від двох хромосом. Власне кажучи, потрібно із двох векторів речовинних чисел одержати нові вектори за якими-небудь законами. Більшість real-coded алгоритмів генерують нові вектори в околиці батьківських пар. Далі представлені прості й популярні кросовери.

Нехай C1=(c₁₁,c₂₁,...,c_n1) і C2=(c₁₂,c₂₂,...,c_n2) - дві хромосоми, обрані оператором селекції для схрещування. Після формули для деяких кросоверов приводиться малюнок - геометрична інтерпретація його роботи. Передбачається, що c_k¹<=c_k² якщо f(C1)>=f(C2).

Плоский кросовер (flat crossover): створюється нащадок H=(h₁,…,h_k,…,h_n), де h_k, (k=1,…,n)– випадкове число з інтервалу [c_k1,c_k2].

Найпростіший кросовер (simple crossover): випадковим образом вибирається число k з інтервалу {1,2,…,n-1}, генеруються два нащадки H1=(c₁¹,c₂¹,…,c_k¹,c_k+1²,…,c_n²) і H2=(c₁²,c₂²,…,c_k²,c_k+1¹,…,c_n²)...

Арифметичний кросовер (arithmetical crossover): створюються два нащадки H1=(h₁¹,…,h_n¹), H2=(h₁²,…,h_n²), де h_k¹=w*c_k¹+(1-w)*c_k², h_k²=w*c_k²+(1-w)*c_k¹, k=1,…,n; w або константа (рівномірний арифметичний кросовер) з інтервалу [0;1], або змінюється зі збільшенням епох (нерівномірний арифметичний кросовер).

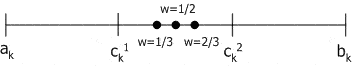
Рис. 2.1. Арифметичний кросовер.

Геометричний кросовер (geometrical crossover): створюються два нащадки H1=(h₁¹,…,h_n¹), H2=(h₁²,…,h_n²), де h_k1=(с_k¹)w*(c_k²)(1-w), (c_k²)w*(c_k¹)(1-w), де w – випадкове число з інтервалу [0;1].

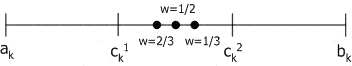
Рис. 2.2. Геометричний кросовер.

Змішаний кросовер (blend, BLX-alpha crossover): генерується один нащадок H=(h₁,…,h_k,…,h_n), де h_k – випадкове число з інтервалу [c_min–I*alpha,c_max+I*alpha], c_min=min(c_k¹,c_k²), c_max=max(c_k¹,c_k²), I=c_max–c_min. BLX-0.0 кросовер перетворюється в плоский.

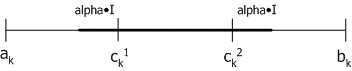
Рис. 2.3. Змішаний кросовер.

Лінійний кросовер (linear crossover): створюються три нащадки Hq=(h₁^q,…,h_k^q,…,h_n^q), q=1,2,3, де h_k¹=0.5*c_k¹+0.5*c_k², h_k²=1.5*c_k¹-0.5*c_k², h_k³=–0.5*с_k¹+1.5*c_k². На етапі селекції в цьому кросовере відбираються два найбільш сильні нащадки.

Рис. 2.4. Лінійний кросовер.

Дискретний кросовер (discrete crossover): кожний ген h_k вибирається випадково за рівномірним законом з кінцевої множини {c_k¹,c_k²}.

Рис. 2.5. Дискретний кросовер.

Розширений лінійний кросовер (extended line crossover): ген h_k=c_k¹+w*(c_k²–c_k¹), w – випадкове число з інтервалу [-0.25;1.25].

Рис. 2.6. Розширений лінійний кросовер.

Евристичний кросовер (Wright’s heuristic crossover). Нехай C1 - один із двох батьків із кращою пристосованістю. Тоді h_k=w*(c_k¹-c_k²)+c_k¹, w - випадкове число з інтервалу [0;1].

Рис. 2.7. Евристичний кросовер.

Нечіткий кросовер (fuzzy recombination, FR-d crossover): створюються два нащадки H1=(h₁¹,…,h_n¹), H2=(h₁¹,…,h_n²)... Імовірність того, що в i-тім гені з'явиться число v_i , задається розподілом p(v_i) {F(c_k¹),F(c_k²)}, де F(c_k¹),F(c_k²) – розподілу ймовірностей трикутної форми (трикутні нечіткі функції приналежності) з наступними властивостями (c_k¹<=c_k² і I=|c_k¹–c_k²|) таб.2.1.

Параметр d визначає ступінь перекриття трикутних функцій приналежності, за замовчуванням d=0.5.

Таблиця 2.1.

Розподіл імовірностей	Мінімум	Центр	Максимум
F(ck1)	ck1–d*I	ck1	ck1+d*I
F(ck2)	ck2–d*I	ck2	ck2+d*I

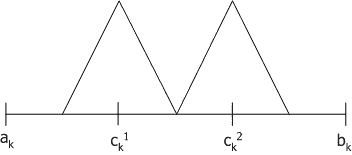
Рис. 2.8. Нечіткий кросовер.

Мін-максний кросинговер

Для представлення хромосоми числами із плаваючою крапкою використається практично тільки мін-максный кросовер або його модифікації:

Для батьків і виходять 4 нащадка

,

,

,

.

Вибираються два кращих із цих чотирьох нащадків.

Розглянуті кросовери історично були запропоновані першими, однак у багатьох завданнях їхня ефективність виявляється невисокою. Виключення становить BLX-кросовер з параметром alpha=0.5 - він перевершує по ефективності більшість простих кросоверів. Пізніше були розроблені поліпшені оператори схрещування, аналітична формула яких і ефективність обґрунтовані теоретично. Один з таких кросоверов - SBX.

SBX кросовер

SBX (англ.: Simulated Binary Crossover) - кросовер, що імітує двійковий. Був розроблений в 1995 році дослідницькою групою під керівництвом K. Deb'а. Як треба з його назви, він моделює принципи роботи двійкового оператора схрещування.

SBX кросовер був отриманий у такий спосіб. У двійкового кросовера була виявлена важлива властивість – середнє значення функції пристосованості залишалося незмінним у батьків і їхніх нащадків, отриманих шляхом схрещування. Потім автором було уведене поняття сили пошуку кросовера (search power). Це кількісна величина, що характеризує розподіл імовірностей появи будь-якого нащадка від двох довільних батьків. Спочатку була розрахована сила пошуку для однокрапкового двійкового кросовера, а потім був розроблений речовинний SBX кросовер з такою же силою пошуку. У ньому сила пошуку характеризується розподілом імовірностей випадкової величини :

Для генерації нащадків використовується наступний алгоритм, що використовує вираження для P( ) . Створюються два нащадки H_k=(h_1k, …, h_jk, …, h_nk), k=1,2, де , , – число, отримане по формулі:

У формулі u(0,1) – випадкове число, розподілене за рівномірним законом, n [2,5] – параметр кросовера.

На малюнку наведена геометрична інтерпретація роботи SBX кросовера при схрещуванні двох хромосом, що відповідають речовинним числам 2 і 5. Видно, як параметр n впливає на кінцевий результат: збільшення n спричиняє збільшення ймовірності появи нащадка в околиці батька й навпаки.

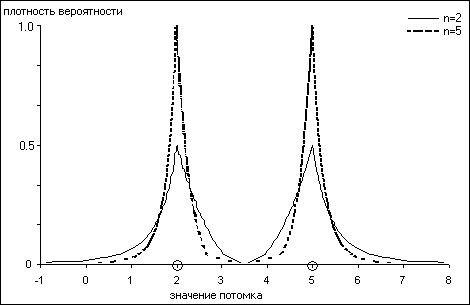
Рис. 2.9. SBX кросовер.

Експерименти автора SBX кросовера показали, що він у багатьох випадках ефективніше BLX, хоча, напевно, не існує жодного кросовера, ефективного у всіх випадках. Дослідження показують, що використання декількох різних операторів кросовера дозволяє зменшити ймовірність передчасної збіжності, тобто поліпшити ефективність алгоритму оптимізації в цілому. Для цього можуть використатися спеціальні стратегії, що змінюють імовірність застосування окремого еволюційного оператора залежно від його «успішності», або використання гібрідних кросоверов, яких у цей час налічується кілька десятків.