Оператор кросинговера (схрещування)

Простий оператор кросинговеру (ОК) із заданою вірогідністю P_c виконується в 3 етапи:

1-й етап. Дві хромосоми (батьки)

A=

B=

вибираються випадково з проміжної популяції, сформованої за допомогою оператора репродукції (ОР).

2-й етап. Випадково вибирається точка схрещування - число k із діапазону [1,2,n-1], де n – довжина хромосоми (число біт в двійковому коді )

3 -й етап. Дві нові хромосоми A', B' (нащадки) формуються з A і B обміном підрядків після точки схрещування:

A=

B=

Наприклад, розглянемо виконання кросинговеру для хромосом 1 і 2 з проміжної популяції:

A=0 1 1 0 1

B=1 1 0 0 0

1  k  4, k=4

A=0 1 1 0 0

B=1 1 0 0 1

Слід зазначити, що ОК виконується із заданою вірогідністю P_c (відібрані дві хромосоми не обов'язково схрещуються). Зазвичай величина .

Таким чином, оператори репродукції і схрещування дуже прості – вони виконують копіювання хромосом і частковий обмін частин хромосом. Продовження нашого прикладу представлено на рис.1.3 у другій таблиці (кросинговер).

Порівняння з попередньою таблицею показує, що в проміжній популяції після схрещування покращилися всі показники популяції (середнє і максимальне значення ЦФ) .

Мутація

Далі згідно алгоритму класичного ГА із заданою вірогідністю виконується оператор мутації. Інколи цей оператор грає вторинну роль. Зазвичай вірогідність мутації мала -

Оператор мутації (ОМ) виконується в 2 етапи:

1-й етап. У хромосомі A= випадково вибирається k-а позиція (бит) мутации ( 1  k  n ).

2-й етап. Проводиться інверсія значення гена в k -й позиції.

.

Наприклад, для хромосоми 11011 вибирається k=3 і після інверсії значення третього біта виходить нова хромосома – 11111. Продовження нашого прикладу представлене в третій таблиці (мутація) рис.1.3. Таким чином, в результаті роботи генетичних операторів знайдено оптимальне рішення x=31.

В даному випадку, оскільки приклад штучно підібраний, ми знайшли оптимальне рішення за одну ітерацію. У загальному випадку ГА працює до тих пір, поки не буде досягнутий критерій закінчення процесу пошуку і в останньому поколінні визначається краща хромосома.

Представлення рішень в двійковій формі

У попередньому прикладі ми розглядали лише цілочисельні рішення. Узагальнимо ГА на випадок дійсних чисел на наступному прикладі, в якому для функції

f(x)=(1,85 -х)*cos(3,5x – 0,5),

представленою на рис.1.5 необхідно знайти , яке максимізувало f, тобто таке , для якого для всіх х .

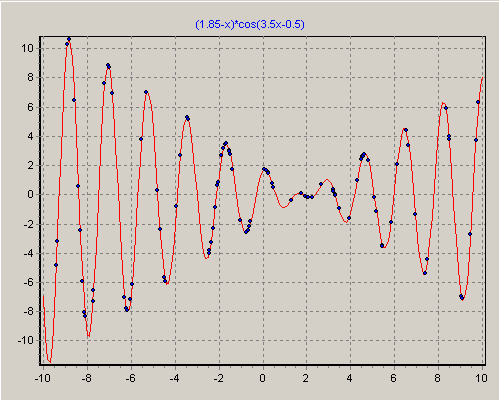
Рис.1.5. Приклад функції з популяцією хромосом на початку еволюції

Нам необхідно побудувати ГА для вирішення цього завдання. Для представлення рішення (хромосоми) використовуватимемо двійковий вектор, який застосовується в класичному простому ГА. Його довжина залежить від необхідної точності рішення, у даному випадку визначемо 3 знаки після коми.

Оскільки відрізок області рішення має довжину 20, для досягнення заданої точності відрізок [-10,+10] має бути розбитий на рівні частини, число яких має бути не менше ніж 20*1000. Використовуємо двійковий код номера відрізка. Цей код дозволяє визначити відповідне йому дійсне число, якщо відомий діапазон рішення. Звідси витікає, що двійковий вектор для кодування рішення повинен мати 15 біт, оскільки

16384= <20000

Це дозволяє розбити відрізок [-10,+10] на 32768 частин і забезпечити необхідну точність. Відображення з двійкового коду ( ) ( ) в дійсне число у діапазоні [-10,+10] виконується в два кроки.

1. Переклад двійкового числа в десяткове:

2. Обчислення відповідного дійсного числа х:

, де – 10 лівий край діапазону рішення.

Хромосоми (000000000000000) і (111111111111111) представляють кінцеві значення діапазону –10 і +10 відповідно.

Вочевидь, при даному двійковому представленні дійсних чисел можна використовувати класичний простий ГА. На рис.1.5–рис.1.8 представлено розташування хромосом - потенційних рішень на різних етапах ГА в процесі пошуку рішення. На рис. 1.5 показана початкова популяція потенційних рішень, яка рівномірно покриває зону пошуку рішення. Далі поступово із збільшенням номера покоління особини "конденсуються" близько до екстремумів і наприкінці знаходиться краще рішення.

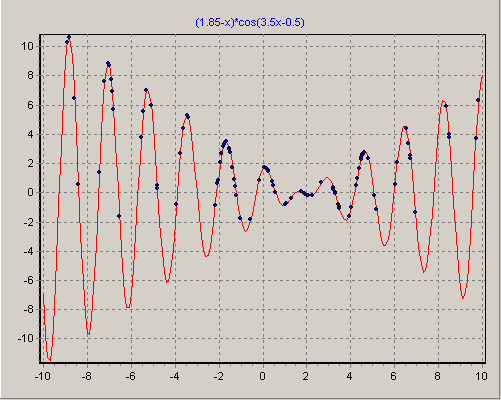
Рис.1.6. Положення хромосом у початковій популяції

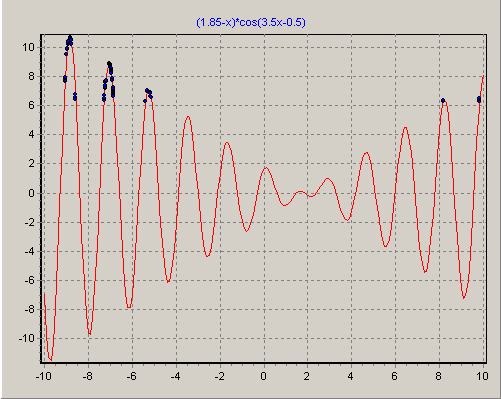Рис.1.7. «Конденсація» особин в околицях екстремумів

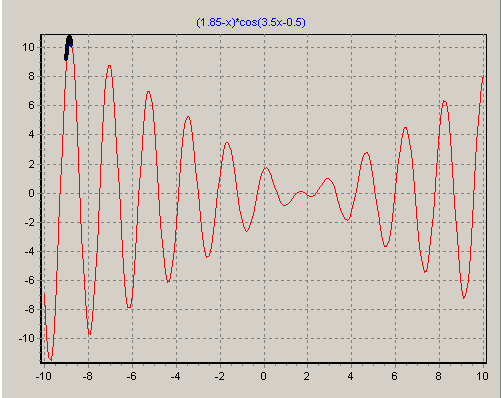
Рис.1.8. Положення хромосом популяції в кінці еволюції