Генетичні оператори

Розглянемо роботу простого ГА на наступному прикладі. Треба знайти (для простоти) цілочисельне значення х в інтервалі від 0 до 31, при якому функція приймає максимальне значення.

Т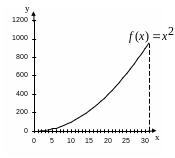 ут хромосоми початкової популяції (двійкові коди значень змінних х - стовпець 2) згенерували випадковим чином. Двійковий код значення х називається хромосомою (вона представляє генотип). Популяція утворює множина потенційних рішень даної проблеми. У третьому стовпці представлені їх десяткові значення (фенотип). Далі на цьому прикладі проілюструємо роботу трьох основних генетичних операторів.

Рис.1.2. Приклад функції

Початковий етап роботи ГА для даного прикладу приведений у верхній таблиці (репродукція) рис.1.3.

Репродукція

Репродукція – це процес, в якому хромосоми копіюються в проміжну популяцію для подальшого "розмноження" згідно їх значенням цільової (фитнес-) функції. При цьому хромосоми з кращими значеннями цільової функції мають велику вірогідність попадання одного або більш разів у наступне покоління.

Репродукція

№ хромосоми	Початкова популяція особин	Десяткове значення x	Значення f(x)		Середнє значення	Максимальне значення f max (x)
1	01101	13	169	0,14	293	576
2	11000	24	576	0,49
3	01000	8	64	0,06
4	10011	19	3 61	0,31

Кросинговер

№ хромосоми	Популяція після репродукції	Десяткове значення x	Значення f(x)	Пари хромосом для кросинговеру	Середнє значення	Максимальне значення f max (x)
1	0 1 1 0 1	13	169	1-2	439	729
2	1 1 0 0 0	24	576	1-2
3	1 1 0 0 0	24	576	3-4
4	1 0 0 1 1	19	3 61	3-4

Мутація

№ хромосоми	Популяція після кросинговеру	Нова популяція після мутації	Десяткове значення x	Значення f(x)	Середнє значення	Максимальне значення f max (x)
1	01100	01100	12	144	496.5	961
2	11001	11001	25	625
3	11011	11111	31	961
4	10000	10000	16	256

Рис.1.3. Еволюція популяції

В очевидь, оператор репродукції (ОР) є штучною версією природної селекції – виживання сильних за Дарвіном. Цей оператор представляється в алгоритмічній формі різними способами. Найпростіший (і популярний) метод реалізації ОР – побудова колеса рулетки, в якій кожна хромосома має сектор, пропорційний значенню ЦФ. Для нашого прикладу "колесо рулетки" має наступний вигляд, представлений на рис.1.4.

Для селекції хромосом використовується випадковий пошук на основі колеса рулетки. При цьому колесо рулетки обертається і після останову її покажчик визначає хромосому для селекції в проміжну популяцію (батьківський пул). Вочевидь, що хромосома, якій відповідає більший сектор рулетки, має велику вірогідність попасти в наступне покоління. В результаті виконання оператора репродукції формується проміжна популяція, хромосоми якої будуть використані для побудови покоління за допомогою операторів схрещування.

У нашому прикладі вибираємо хромосоми для проміжної популяції, обертаючи колесо рулетки 4 рази, що відповідає потужності початкової популяції. Величину 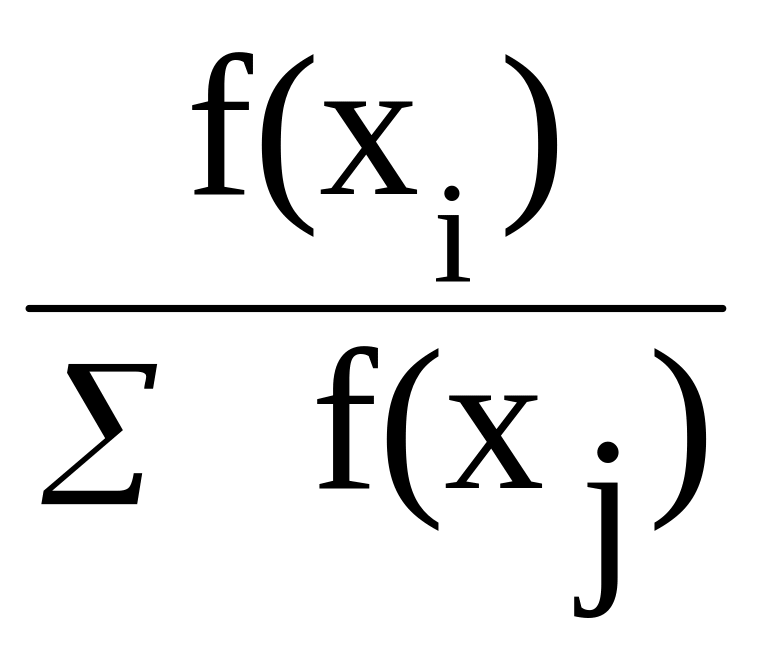позначимо, як , тоді очікувана кількість копій i-ої хромосоми визначається M= *N, N - потужність популяції. Число копій хромосоми, перехідних в наступне покоління, інколи визначається і так:

,

де - середнє значення хромосоми в популяції.

Розрахункові числа копій хромосом за приведеними формулами наступні: хромосома 1 - 0,56; хромосома 2 - 1,97; хромосома 3 – 0,22; хромосома 4 – 1,23. В результаті, в проміжну популяцію 1-а хромосома потрапляє в одному екземплярі, 2-а – в двох, 3-я – зовсім не потрапляє, 4-а – в одному екземплярі. Отримана проміжна популяція є початковою для подальшого виконання операторів кросинговеру і мутації.