Деревовидна структура

Я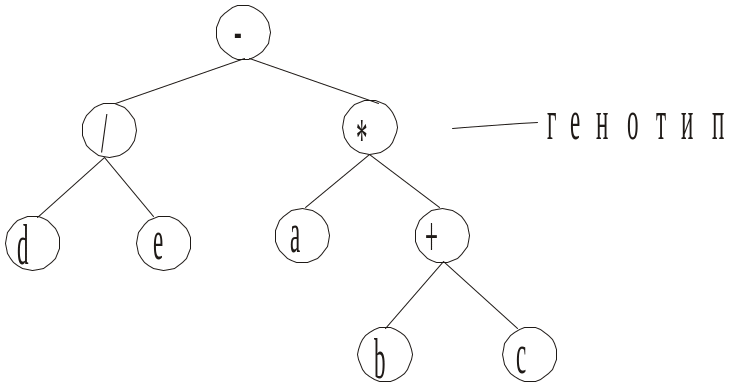 к приклад розглянемо арифметичну формулу, яку зручно представляти деревом. Розглянемо арифметичну формулу . Відзначимо, що дерево (генотип) рис.4.1 також представляє цю формулу (фенотип) .

Рис.4.1 Деревовидне представлення формули .

При цьому листя дерева відповідають терміналам, а внутрішні вузли - функціям.

Деревовидна форма представлення генотипу виявляється для даного класу завдань ефективнішою, і дозволяє працювати з програмами різної довжини. Важливим аспектом є використання пам'яті при виконанні програми. Деревовидна структура дозволяє використовувати лише локальну пам'ять в процесі виконання. Локальність пам'яті вбудована в саму деревовидну структуру. Значення змінних доступні для функції лише в дереві, корінню якого відповідає функція. Наприклад, значення змінних d, e є локальними відносно вузла ‘/’.

Лінійні структури

Розглянемо один з можливих варіантів лінійної структури ГП, орієнтованого на програмування на мові С. При цьому кожна хромосома (програма) представлена послідовністю змінної довжини операторів С. Нижче представлений приклад такої програми.

void int u

double v[8]

{

.

v[0]=v[5]+75;

v[7]=v[0]-69;

if (v[1]>0)

if (v[4]>21)

v[4]=v[2]*v[1];

v[2]=v[5]+v[4];

v[6]=v[4]-4;

v[1]=sin(v[6]);

if(v[0]>v[1])

v[5]=v[7]+115;

if(v[1]<=v[6])

v[1]=sin(v[7]);

}

Тут функціональна множина складається з арифметичних операцій, умовних операторів if і викликів функцій.

Змінні і константи разом утворюють множину термінальних символів. Таким чином будь-який оператор кодується 4-х мірним вектором, компонентами якого є тип оператора (одна компонента) і адреси змінних і констант.

Наприклад, оператор vi=vj+c представляється вектором (+,i,j,c). Кожна компонента використовує 1 байт пам'яті, отже, число змінних (і констант) обмежено зверху 256.

Графоподібні структури

Розглянемо типову блок-схему програми, яка представлена на рис.4.2.

Тут кожна хромосома - програма представляється у вигляді графа. Вершина графа представляє лінійну частину програми, яка має 2 частини - власне лінійну програму і вузол галуження. З рисунка видно, що блок-схема лінійного графа природніша, ніж лінійна (деревовидна) форма представлення програми.

Це пояснюється тим, що багато програм містять оператори галуження, після яких може бути виклик іншої частини коду програми, що не входить в лінійну послідовність операторів. Лінійна програма виконується у тому випадку, коли досягається даний вузол графа при інтерпретації програми на конкретних даних. Після виконання лінійної частини вибирається вузол-послідовник відповідно до функції галуження цього вузла. Протягом інтерпретації вузли лише одного шляху графа від входів до виходу виконуватимуться залежно від поточних значень змінних умов операторів галуження.

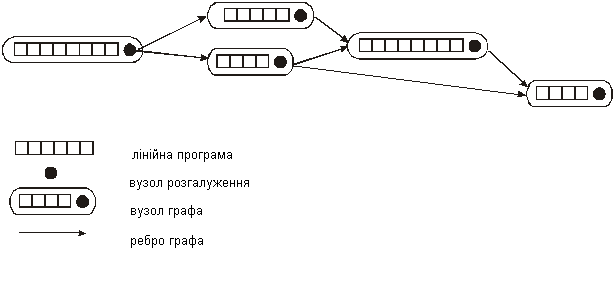
Рис.4.2. Представлення програми у вигляді графа.

Реалізація лінійних підструктур використовує список операторів С (або іншої мови програмування) змінної довжини, які оперують із змінними або константами і отримані значеня привласнюються змінним. Після виконання програми, обчислені значення запам'ятовуються у “вихідні” змінні.

Функція галуження також є оператором С, який оперує з тими ж змінними, що і лінійна програма, але цей оператор лише читає значення цих змінних.

На рис.4.3 детально представлено вузол графа, що відповідає деякій частині лінійної програми.

Рис.4.3. Підпрограма, відповідного вузла графа.

Дана модель, як і попередня, використовує при виконанні програми глобальну пам'ять. Графоподібні структури дозволяють розширити клас завдань, які можуть бути вирішені за допомогою ГП, оскільки є загальнішими в порівнянні з першими двома і допускають ефективну реалізацію.

Інший спосіб вживання структур графів в ГП називається PADO. Тут кожна програма представляється орієнтованим графом, що містить вузли, індексовану пам'ять для вхідних змінних і стек, як показано на рис.4.4. У довільному орієнтованому графі кожен вузол може мати N дуг, що витікають.

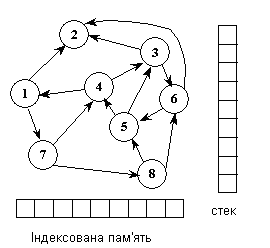
Рис.4.4. Представлення програми орієнтованим графом.

Ця структура не просто показує потоки інформації і управління ходом виконання програми. Вузол в графі відповідає сегменту програми і має дві частини: «дія» і «галуження». Частина «дія» містить константи і функцію, яка виконується при досягненні даного вузла в процесі інтерпретації програми. Дані передаються між вузлами через стек. Частина «дія» отримує дані з (верху) стека і після виконання відповідної функції передає перетворені дані знову в стек. Після цього виконується «галуження», яке визначає частину наступного виконуваного вузла на підставі даних стека, пам'яті або спеціальних констант галуження. Вочевидь, що в процесі інтерпретації необов'язково відвідуються всі вершини графа. Кожна програма має дві спеціальні вершини «старт» і «кінець» і окрім цього може містити деякі спеціальні вузли типа «виклик підпрограми». Оскільки граф може містити зворотні зв'язки, то вершина «кінець» на деяких вхідних даних може бути недосяжною унаслідок «зациклення». Тому необхідно контролювати і обмежувати час виконання програми.