г

Рис. 6

Дифракция Кирхгофа. 2. Дифракция Френеля.

3. Дифракция Фраунгофера.

де , . Величины и носят названия пространственных частот. При таких обозначениях выражение (15) формально совпадает с выражением для спектрального разложения электрических сигналов. Оказывается, что эта аналогия далеко не формальна и выражение (15) лежит в основе Фурье – оптики и оптической обработки информации. Таким образом, дифракцию Фраунгофера можно наблюдать в фокальной плоскости линзы (рис. 6). Заметим, что волновой фронт в фокальной плоскости плоский. Вблизи фокальной плоскости выполняются условия дифракции Френеля и вдали от нее – условия для дифракции Кирхгофа. Видно, что отклонения от геометрической оптики в случае дифракции Кирхгофа минимальны. Этот рисунок иллюстрирует неприемлемость приближения геометрической оптики вблизи фокальной плоскости – если луч определить как нормаль к волновому фронту, то вблизи линзы луч наклонен к оси, а в фокальной плоскости он ей параллелен. Таким образом, наблюдается отклонение от прямолинейного распространения.

Так как размер дифракционной картины мал, то ее удобно наблюдать через окуляр. Такая двухкомпонентная система является зрительной трубой (рис.6).

Примеры дифракции

Дифракция на прямоугольном отверстии и щели. Рассмотрим дифракцию на прямоугольном отверстии. Для расчета распределения освещенности в фокальной плоскости необходимо воспользоваться дифракционным интегралом в приближении Фраунгофера

			(1)

(2)

г

Рис.1

де - прямоугольная область (рис. 1). Полагая, что отверстие освещается параллельным пучком с равномерным распределением освещенности , запишем двойной интеграл как повторный, который вычисляется без труда

Распределение освещенности получится возведением в квадрат (2). Выбирая так, чтобы , запишем выражение для

,

(3)

г

Рис. 2

де ; - здесь пространственные частоты и выражены через координаты в фокальной плоскости и . Из (3) следует, что распределение освещенности есть произведение двух аналогичных функций, каждая из которых есть функция только одной координаты. Из очевидных равенств и следует, что каждая из них есть сечение двумерной функции распределения. Исследуем, для определенности первое из них. График этой функции приведен на рис 2. Нули, они же и минимумы, можно найти из условия откуда

(5)

так как из следует, что , и в выражении (4) возникает неопределенность типа , представляющая собой замечательный предел, равный 1. Именно этим объясняется глобальный, главный максимум при . Выражения для минимумов получатся из (5)

.

(6)

О

Рис. 3

стальные максимумы, называемые побочными, можно определить из условия . Вычисляя производную, найдем уравнение

для максимумов

,

(7а)

откуда

.

(7б)

Полученное уравнение не имеет аналитического решения, но результат можно получить графически (рис.3). Из этого рисунка видно, что ординаты точек пересечения близки к и при стремятся к этим значениям. Таким образом, можно считать, что положения точек максимумов примерно равны

.			(8)

.

(9)

П

Таблица 1.

1		0,047
2		0,017
3		0,008
4		0.003

римерные значения освещенности в максимумах можно определить комбинирую соотношения (3), (7б) и (8). Учитывая равенство , получим

Зависимость интенсивностей побочных максимумов относительно интенсивности главного максимума приведена в таблице 1.

Рис. 4

Если рассматривать двумерную картину дифракции, то из выражений для максимумов и минимумов (5) и (8), расстояние между побочными максимумами обратно пропорциональны ширине прямоугольного отверстия в этом направлении, т.е. дифракционная картина как бы растягивается в стороны больших сторон прямоугольника и, соответственно, сжимается со стороны меньших (рис. 4а). При дифракции на щели, которую можно считать таким прямоугольным отверстием, у которого одна из сторон значительно меньше другой, дифракционная картина вытягивается в тонкую линию (рис. 4б).

Дифракция на круглом отверстии. Учет дифракции на круглом отверстии имеет большое значение, так как подавляющее большинство оптических приборов имеет оптические элементы круглой формы. Для определения распределения освещенности в дифракционной картине поступим аналогично предыдущему случаю и вычислим дифракционный интеграл Фраунгофера, но областью интегрирования здесь будет круг заданного радиуса .

.

(10)

Удобно перейти в полярную систему координат

(11)

тогда , и интеграл (10) примет вид

.

(12)

Внутренний интеграл выражается через функцию Бесселя

,

(13)

где - функция Бесселя нулевого индекса. Полный интеграл получится в результате интегрирования по , который сводится к табличному интегралу от функции Бесселя. Результат интегрирования не зависит от угловой переменной

,

(14)

где - функция Бесселя первого индекса.

Рис. 5

График сечения функции приведен на рис. 5. Внешне он похож на сечения распределения при дифракции на прямоугольном отверстии. Но так как аргументом этой функции является , то ди­фракционная картина будет состоять из концентрических окружностей и внешне напоминать кольца Ньютона. Однако между этими распределениями есть су­щественные отличия – у колец Ньютона расстояния между кольцами убывают пропорционально корню квадратному их номера², а в рассматри­ваемом случае эти расстояния стремятся к постоянной вели­чине. Кроме того зави­симости интенсив­ностей колец от их радиу­сов сущест­венно отличаются. Распределения интен­сивностей при ди­фракции на круглом от­верстии называется распределением Эри. Минимумы функции определяются нулями функции Бесселя , значения которых совместно с радиусами темных колец сведены в таблицу 2. Туда же внесены и значения максимумов распределения совместно с радиусами светлых колец, которые получены из условия равенства нулю производной, которая равна , откуда получаются из условия , где функция Бесселя второго индекса.

Таблица 2.

Светлые кольца				Темные кольца
№				№
1	5.135	0.817	0.01752	1	3.832	0.6098
2	8.417	1.340	0.00415	2	7.016	1.117
3	11.620	1.849	0.00161	3	10.173	1.619
4	14.796	2.355	0.00078	4	13.324	2.121

По сравнению с дифракцией на прямоугольном отверстии интенсивность побочных максимумов здесь меньше.

Дифракция на периодической структуре. Рассмотрим дифракцию на одномерной периодической структуре, называемой еще решеткой. Пусть ее пропускание описывается комплексной, периодической с периодом в направлении оси , а в направлении - постоянной функцией , т.е.

(8)

Предположим, что на решетку падает световая волна с постоянной амплитудой и плоским волновым фронтом в направлении нормали к решетке. Распределение поля после решетки будет . Если решетка имеет ширину (в направлении оси ) , а длину , где - число элементов решетки (будем считать, что длина решетки в точности равна целому числу элементов), то дифракционный интеграл в этом случае примет вид

(9)

где - область, занимаемая решеткой (область интегрирования), а в постоянную включено значение амплитуды падающего света . Так как не зависит от , то по можно выполнить интегрирование (вынести множитель за знак интеграла по , после чего интеграл по вычисляется без труда). Включив результат интегрирования по в , которая будет зависеть только от , запишем (9) в виде однократного интеграла

.

(10)

Разбивая область интегрирования на отрезки длиной периода , запишем интеграл (10) в виде суммы

.

(11)

Используя периодичность функции (рис. *), выражение (11) можно записать как

.			(12)

.

(13)

Э

Рис.*

то выражение можно преобразовать, используя теорему смещения, которая очень легко доказыва­ется с помощью замены переменной интегрирования

Применяя, получим

(14)

где .

Выражение в квадратных скобках представляет собой геометрическую прогрессию. Суммируя ее, получим

.

(15)

Так как фиксируется лишь интенсивность электромагнитного поля, то для ее определения необходимо взять квадрат модуля (14)

,

(16)

где - так называемая структур­ная функция решетки, представляющая собой распределение освещенности в дифракционной картине от одного элемента структуры.

Из (16) следует то, что распределения всех периодических структур имеют общий характер, описы­ваемый множителем перед интегралом, а конкретный вид распределения определяется выражением . График зависимости приведен на рис(16). Он может быть получен умножением графика на график структурной функции , который является для огибающей. Построим график . Введем безразмерную переменную , т.е. будем исследовать зависимость

(17)

Рис. *

Данная формула представляет собой отношение двух пе­риодических функций, причем период знаменателя , а период числителя в раз меньше, т.е. . Из теории периодических функций, известно, что их отношение также будет периодической функцией с наибольшим у этих функций периодом .

Знаменатель обращается в нуль при

.

(19)

,

(18)

где - целое число, однако в этих точках и числитель об­ращается в нуль, т.е. в этих точках возникает неопределенность типа . Раскрывая ее по правилу Лопиталя, найдем, что значение функции в этих точках равно . Так как , то минимум функции тогда, когда , т.е. при , т.е. при

Числитель функции осциллирует значительнее чем знаменатель, то можно считать, что будет иметь также максимумы приблизительно в тех точках, когда , т.е. при

. (20)

Значения в этих точках будут и при больших значениях (это можно доказать) т.е. их величины значительно меньше, чем у максимумов, положения которых определено (18).

Таким образом, рассматриваемая функция будет иметь главные максимумы, в точках, определяемых условиями

, (21.а)

откуда положения главных максимумов

. (21.б)

По аналогии определим положения максимумов . Они называются побочными (из (20))

(22)

и минимумов

. (23)

Из анализа выражений (21) - (23) следует, что между двумя главными максимумами находится побочных максимума, разделенных минимумами, так как расстояние между побочными максимумами в раз меньше, чем между главными. График этой функции показан на рис 2 а.

Рис.8

Структурная функция, как уже отмечалось, представляет собой дифракционное распределение интенсивности от одного элемента периодической структуры. Это значительно более плавно изменяющаяся функция и ее примерный вид показан на рис 2 б. Наконец, дифракционное распределение от всей структуры показано на рис 2 в и получено как произведение двух верхних графиков.

Из сказанного ясно, что основным параметром, характеризующим дифракционную структуру, является ее пространственный период , именно от него зависят положения главных максимумов. Все остальные параметры дифракционного распределения играют второстепенную роль. Параметр носит название постоянной решетки.

Рассмотрим плоскую одномерную амплитудную дифракционную решетку или, просто дифракционную решетку. Она состоит из ряда прозрачных прямоугольных отверстий шириной и шириной непрозрачной части так, что . Согласно (16), влияние этих параметров скажется через структурную функцию решетки, для чего надо вычислить интеграл

, (24)

где - функция пропускания одного элемента решетки.

. (25)

Этот интеграл представляет собой дифракцию на прямоугольном отверстии и его вид нам известен

. (26)

Его вид приведен на рис 5, а нули выражаются формулами . После определения квадрата модуля полученного выражения и подстановки его в (16), распределение освещенности в дифракционной картине примет вид

(27)

Распределение освещенности от решетки с показан на рис 8. Так как ширина структурной функции об­ратно пропорциональна размеру прозрачной части штриха , то решетке присуще некоторое противоречие: при умень­шении - с одной стороны все большее число главных мак­симумов имеют достаточно большую амплитуду, а с другой - через решетку проходит меньше света. Это особенно важно при использовании дифракционной решетки в качестве дис­пергирующего элемента в спектральных приборах - в них используется зависимость положения главных максимумов от и эта зависимость пропорциональна номеру (порядку) главного максимума. Возможны ситуации, когда минимумы структурной функции совпадают с главными максимумами. Рассмотрим условия их возникновения. Минимумы струк­турной функции возникают при , т.е. при . Сравнивая это выражение с (18), найдем, что это совпадение выполнится при . Именно такой случай представлен на рис 4, где третий главный мак­симум подавлен вторым минимумом структурной функции.
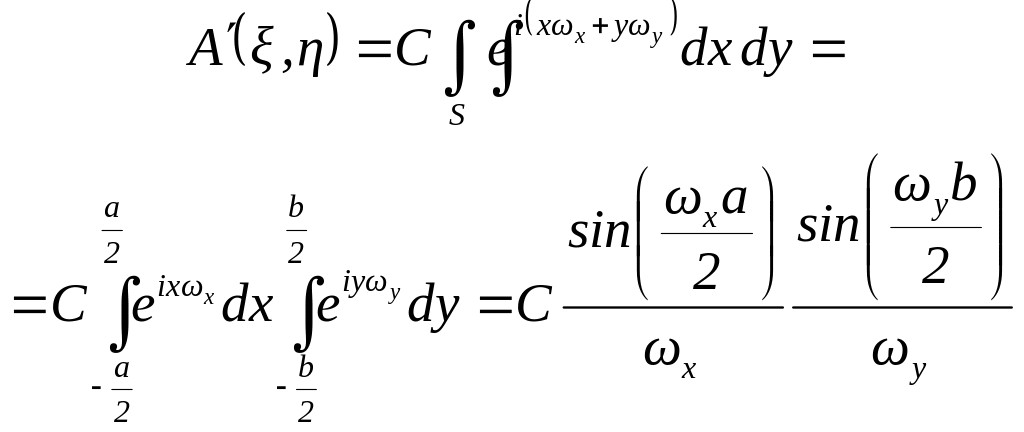
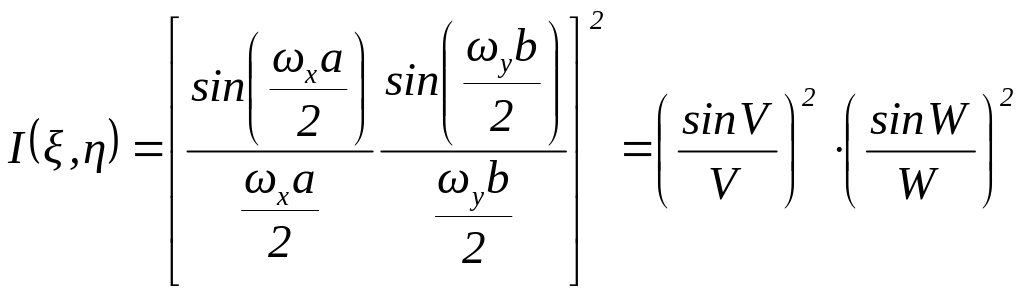
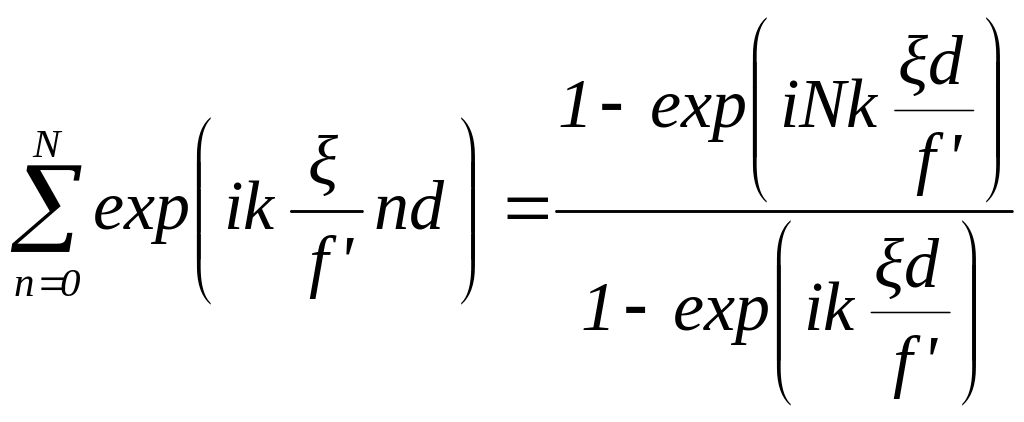