Коефіцієнти ряду Фур’є

Зворотний перехід від ряду (23.2) до ряду (23.1) неважко зробити, визначивши

При визначенні кута Ψ_r потрібно враховувати порізно знаки С_r і В_r, оскільки від них залежить величина кута. Наприклад, при позитивних С_r і В_r їх ставлення позитивно, а кут лежить у першій чверті, при негативних С_r і В_r їх ставлення теж позитивно, але кут знаходиться у третій чверті.

При побудові синусоид по осі абсцис потрібно відкладати початкову фазу R-й гармоніки, перерахувавши її на масштаб основної гармоніки, тобто замість Ψ_r відкласти Ψ_r/R .

Це випливає з того, що градуювання осі абсцис дається в масштабі першої гармоніки, тому на відрізку wt=2п укладається R повних циклів R-й гармоніки.

Коефіцієнти А₀, В_R, С_R ряду (23.2) визначають за допомогою таких формул:

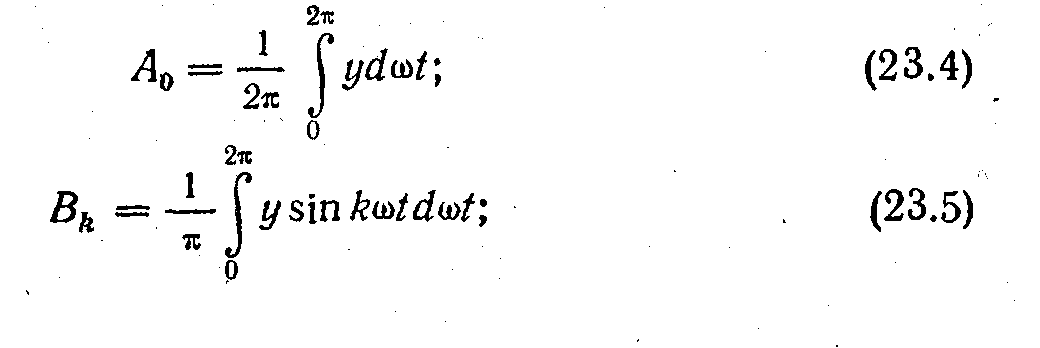
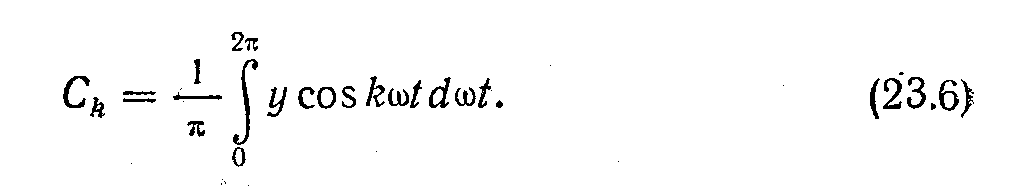
Якщо закон зміни ординат несинусоїдної кривий можна виразити у вигляді рівняння, то вирази (23.4) - (23.6) дозволяють в більшості випадків виконати аналітично розкладання її в тригонометричний ряд виду (23.2) і далі, якщо потрібно, перейти до ряду (23.1). Постійна складова, як видно з формули (23.4), є середнім значенням функції за її період.

Таким чином, постійна складова в тригонометрическом ряду відсутній, якщо середня за період значення функції одно-нуля.

Графо-аналітичний метод визначення коефіцієнтів ряду Фур’є

Коефіцієнти ряду (23.2) можна визначити графо-аналітичним методом, який дає наближені значення коефіцієнтів, але зате є більш загальним, так

як не вимагає аналітичного виразу разлагаемой в ряд функції.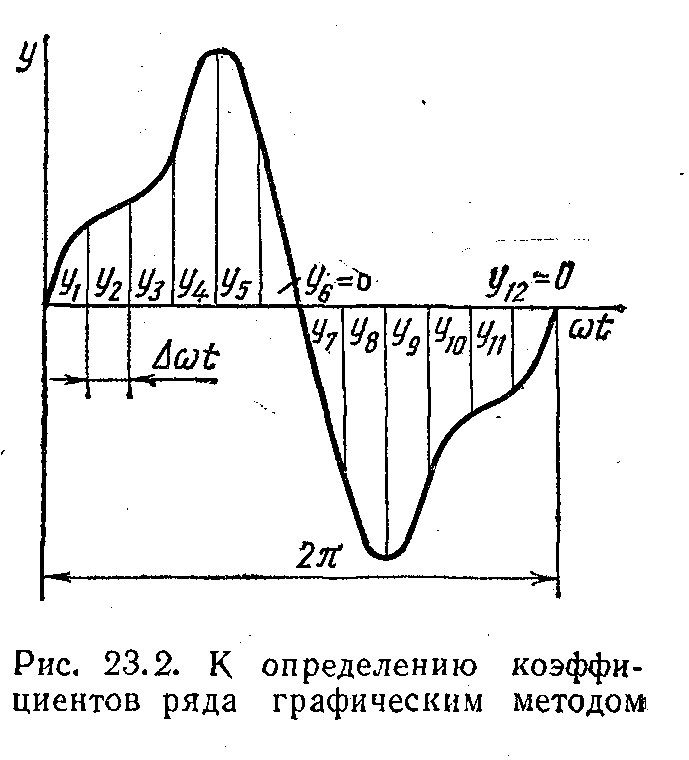

Періодична крива викреслюється на графіку (мал. 23.2). Протягом відрізка, відповідного періоду, на рівних відстанях ∆wt один від 'одного проводяться ординати кривої.

Коефіцієнт А₀ - постійна складова-визначається наближеним виразом

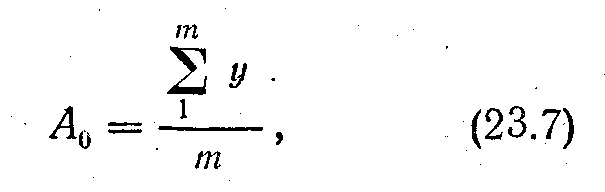
де ∑y- алгебраїчна сума всіх ординат, узята за період; m - число ординат.

Вираз (23.7) следует.из основного (23.4):

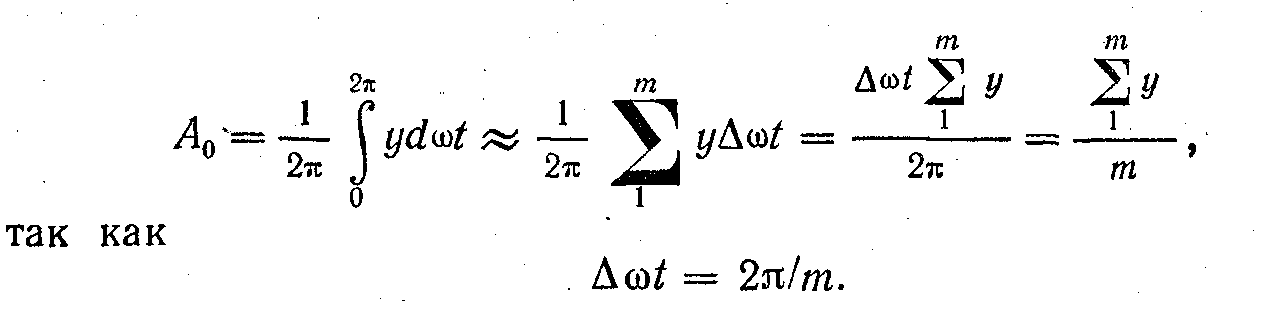
Результат визначення А₀ тим точніше, чим менше буде взято інтервал ∆wt між ординатами.

Аналогічно визначаються коефіцієнти С_r і В_r на підставі виразів (23.5) і (23.6):

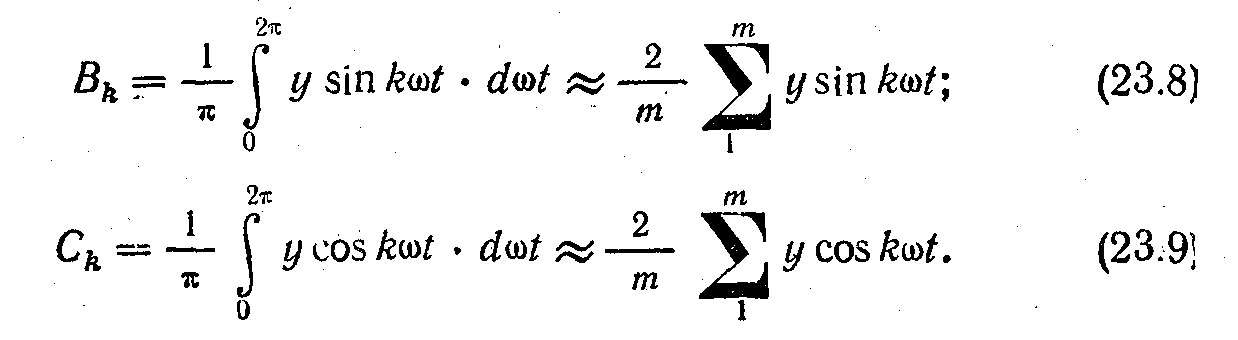
Симетричні несинусоїдальні функції

Періодичні функції, з якими доводиться зустрічатися в електротехніку, найчастіше мають симетрію. Одні з них симетричні щодо осі абсцис, інші - щодо осі ординат або початку координат.

Симетрія несинусоїдних кривих полегшує аналітичне їх вираження.

Функція, симетрична щодо осі абсцис

На рис. 23.4 показаний графік функції, симетричною щодо осі абсцис. Для такого графіка

При симетрії щодо осі абсцис значення функції повторюються із зворотним знаком через половину періоду, тому негативна полуволна, зрушена на половину періоду, є дзеркальним відображенням позитивної напівхвилі.

Як буде показано далі (див. мал. 24.9), таку форму має крива струму в котушки з феромагнітним сердечником при синусоїдної напруги.

У складі тригонометричного ряду функції, що підкоряється співвідношенню (23.11), відсутні постійна складова і гармонійно парного порядку.

У цьому неважко переконатися, якщо записати ряди виду (23.1) для функцій y(wt) і 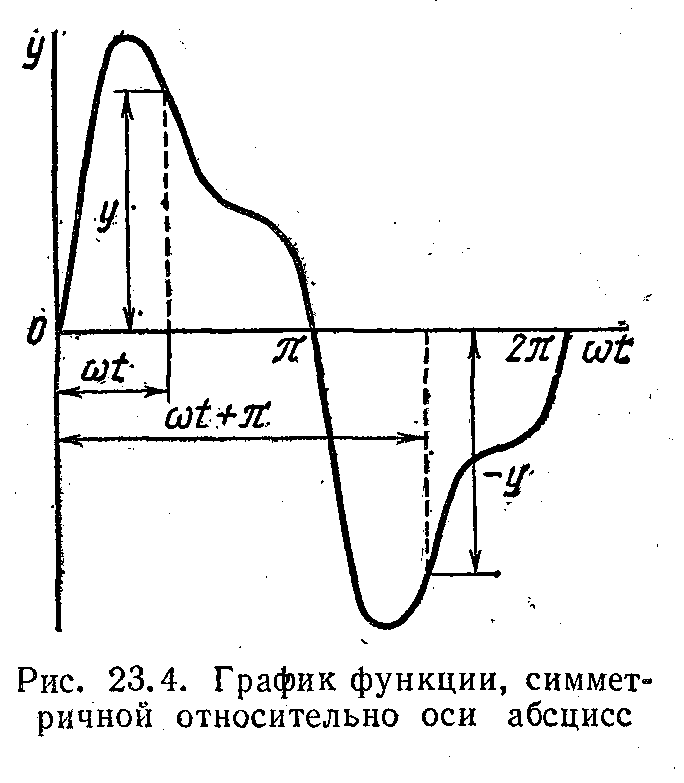y(wt+п)

Функція y(wt+п) відрізняється від y(wt) тим, що всі непарні гармоніки мають негативний знак:

Згідно умові (23.11)

Тоді

При будь-якому wt це рівність можливо, якщо

Таким чином, крива, симетрична щодо осі абсцис, виражається тригонометричним поруч наступного виду:

Або