Індуктивність в системі магнітно-пов'язаних котушок

Розглянемо окремий випадок, коли дві магнітно-пов'язані котушки електрично з'єднані між собою послідовно, у результаті чого в обох котушках струм I один і той же (див. мал. 8.22).

Енергія магнітного поля такої системи

де L=L₁+L₂ ⁺ _- 2М - індуктивність системи магнітно-пов'язаних котушок.

При згодному включення

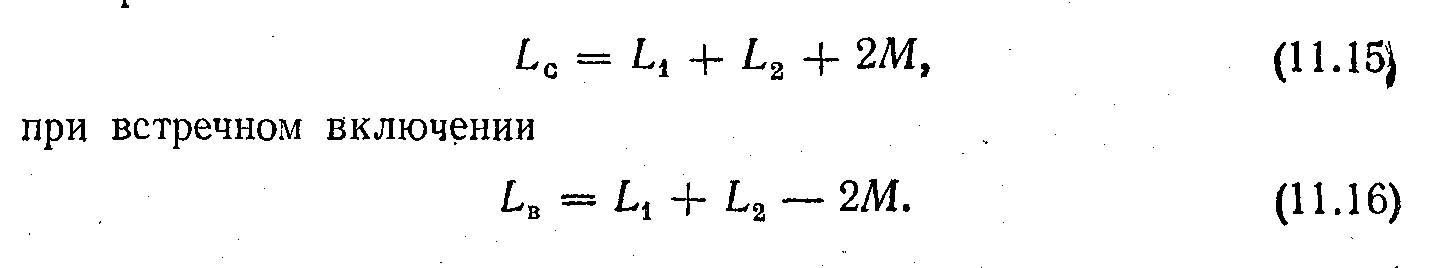
Вираження енергії через характеристики магнитного поля

Формулами (11.13) и (11.14) енергія выражена через характери­стики контурів з токами.

Можна показати, що в даному випадку енергія розподілена в магнітному полі, навколишньому провідники з струмами.

Для прикладу візьмемо поле котушки з кільцевим серцевиною. Якщо діаметр перетину сердечника багато менше діаметра самого сердечника, поле можна вважати рівномірним:

Тут енергія виражена через характеристики магнітного поля, що свідчить про її належності магнітному полю.

Діюча величина змінного струму

При визначенні діючої величини змінного струму можна виходити з якого-або його дії електричного ланцюга (теплового, механічного взаємодії проводів з струмами).

На рис. 12.18 зображені графіки двох струмів: постійного1 і змінного 2, причому величина постійного струму дорівнює амплітуді змінного.

Постійний струм, рівний амплітуді змінного, виділить більше тепла в одному і тому самому елементі ланцюга за один і той же час, так як змінний струм протягом напівперіоду менше постійного, і лише одна мить ці струми рівні.

Діюча величина змінного струму I чисельно дорівнює величині постійного струмуI , який в одному і тому самому елементі ланцюга за час періоду Т виділяє стільки ж тепла, скільки при тих оці умовах виділяє змінний струм.

Діюча величина змінного струму I менше амплітуди (пряма 3 на рис. 12.18).

Визначимо кількість тепла, що виділяється за період Т постійним струмом,

рівним I, і змінним струмом i=I_msinwt (див. мал. 12.18) у елементі ланцюга з опором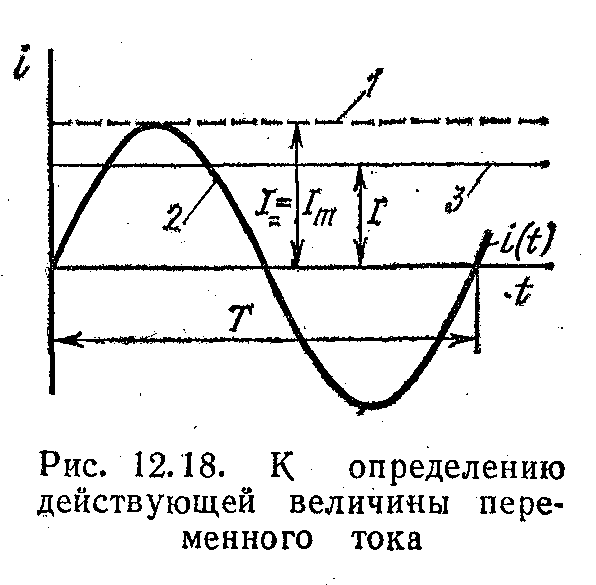 R:

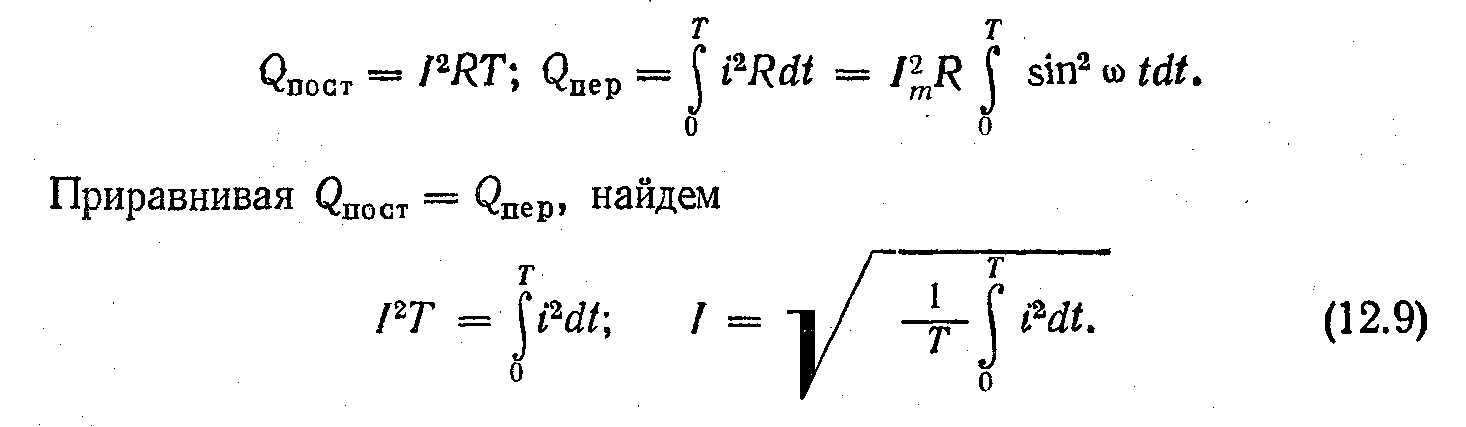
Діюча величина періодичного струму є його середньої квадратичної за період.

Її можна знайти з рівняння (12.9), але для наочності наведемо графічним рішенням поставленої задачі.

Среднеквадратичную величину змінного струму за період можна представити у вигляді квадратного кореня з суми дуже великого числа ординат кривий і²(t), розділеною на число ординат n:

де в чисельнику підкореневої вираження представлена сума квадратів ряду миттєвих струмів протягом періоду, n - число цих значень, прагне до ∞.

На рис. 12.19 показані ряд положень обертового з кутовою швидкістю w вектора струму I_m,і відповідні їм миттєві струми i. Ці положення точками 0, 1, 2 і т. д. на колі, яку описує кiнець вектора I_m.

Розглянемо два положення вектора I_m (точками 2 і 8), віддалені по колу на 90°, тобто перебувають відповідно в першому і другому кварталах кола. Прямокутні трикутники

6'-2-2' i 6'-8-8' рівні, так як рівні їх боки: 2-2' = 6'-8' i 2'-6'= 8-8'. З цих трикутників слідує :

i₂² + I²₈=I_m²

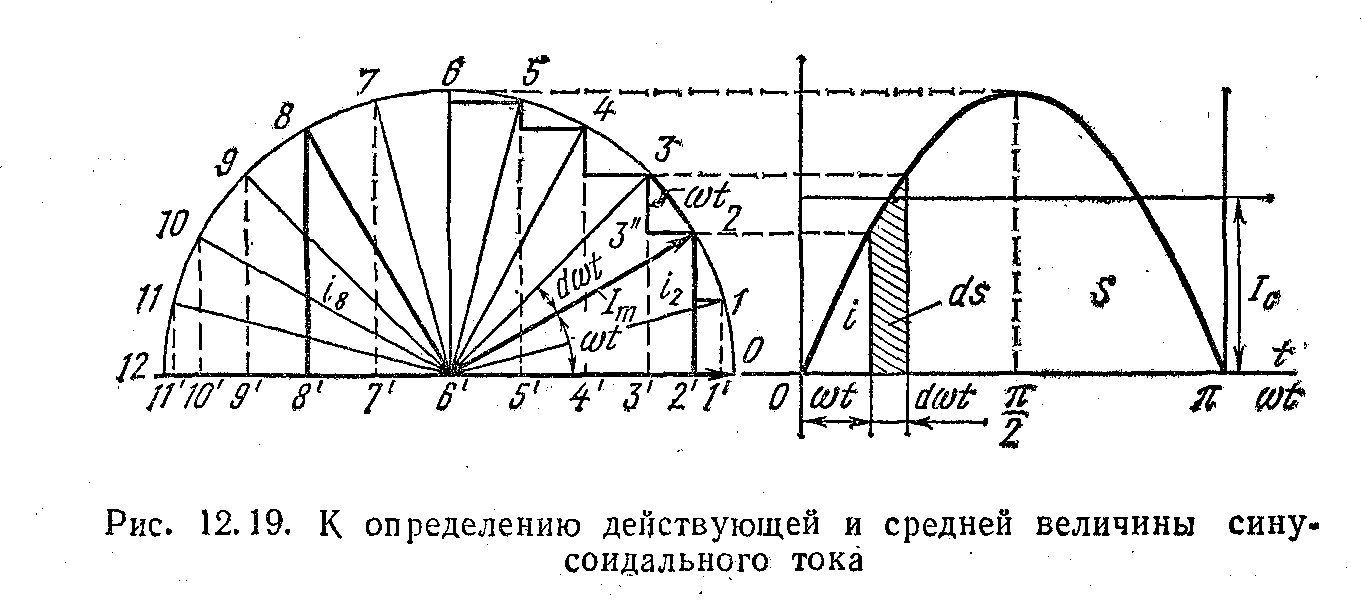
Кожному положенню вектора I_m у першій чверті відповідає інше його положення у другій, для яких можна написати аналогічне вираз. Такі міркування можна провести для іншої полуокружности, тобто поширити їх на другий напівперіод струму, причому квадрати негативних миттєвих струмів будуть позитивні, тому

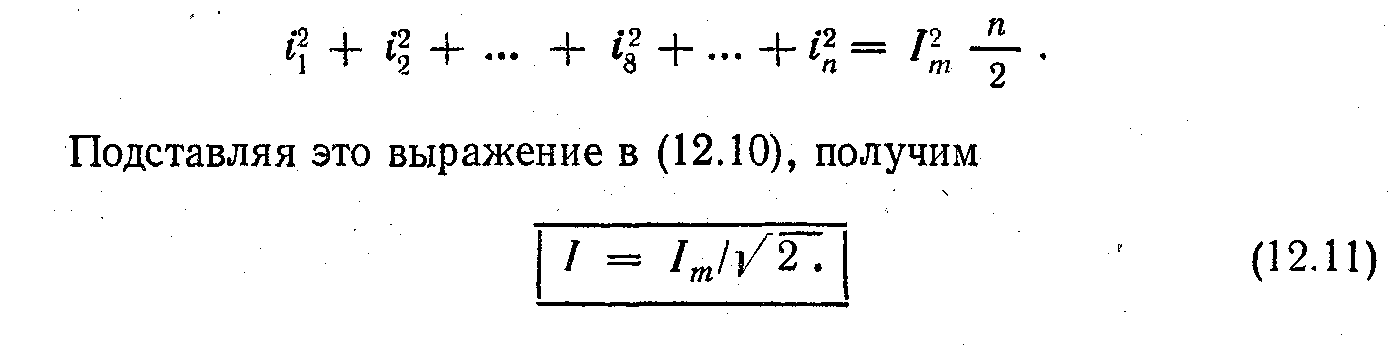
Таким чином, діюча величина синусоїдального струму менше його амплітуди в рази.

Поняття про діючої величиною можна поширити на всі синусоїдальні функції і, отже, говорити про діючої величиною напруги, е. р. с.

Діючі величини струму, напруги вимірюються електровимірювальними приладами. Номінальні струми і напруги електротехнічних пристроїв виражаються діючими величинами. Ввівши поняття про діючої величиною, надалі векторні діаграми будемо будувати для діючих величин напруг і струмів.

Відношення амплітуди до діючої величиною називається коефіцієнтом амплітуди K_a Для синусоїдальної функції цей коефіцієнт дорівнює ; якщо крива струму або напруги має більш гостру форму, ніж синусоїда, то Ка> , інакше K_a< (при прямокутної форми K_a = 1).