Глава 10. Несобственные (обобщенные) интегралы (Интегрирование на некомпактном промежутке)

Ранее был рассмотрен определенный интеграл, необходимым условием существования которого являлось условие ограниченности подынтегральной функции на отрезке . При этом подразумевалось, что отрезок интегрирования конечный, или как его называют компактный. Такие интегралы в противоположность тем, которые будут рассматриваться в этом разделе, иногда, называют собственными.

df.1 Компактным промежутком будем называть -ой сегмент .

df.2 Пусть - полуинтервал числовой прямой , причем ” в ” может быть , символами , а функция интегрируема на сегменте .

df.3 Пусть f(x) – определена на промежутке и f(x) , тогда предел

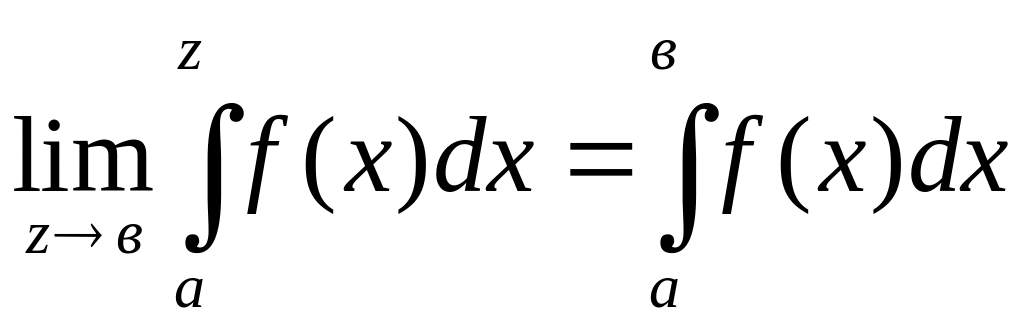(1)

называют несобственным интегралом от функции f(x) на промежутке , если этот предел и конечен.

Очевидно возможны 2 частных случая:

1) Интеграл с бесконечным верхним пределом:

, .

2) Интеграл от неограниченной функции:

, в=const в этом случае

Заметим, что если (ограничена), тогда получаем обычный интеграл Римана. В силу непрерывности функции на (т.е. ), т.е.

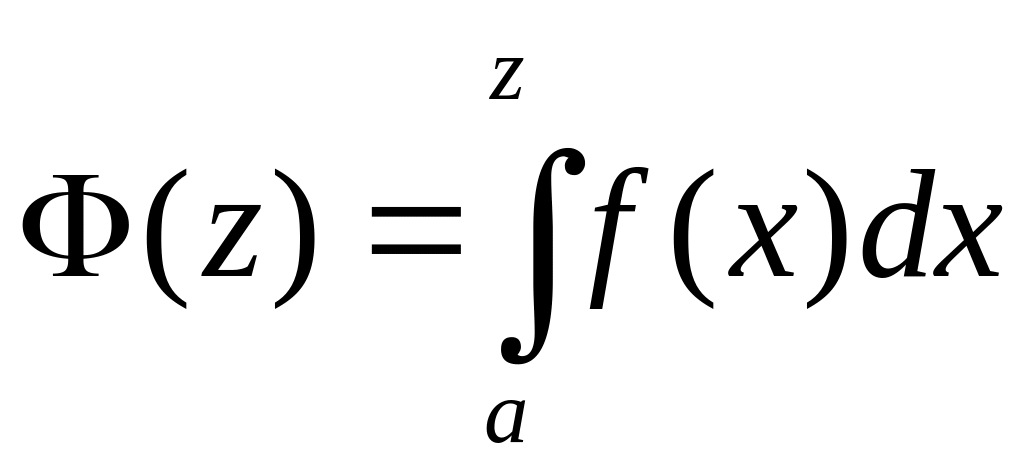
df.4 Пусть f(z) определена на промежутке . ( ) и . Тогда предел

(2)

называется несобственным интегралом от функции f(x) на , если предел и конечен.

Опять возможны два случая:

1. с бесконечным нижним пределом:

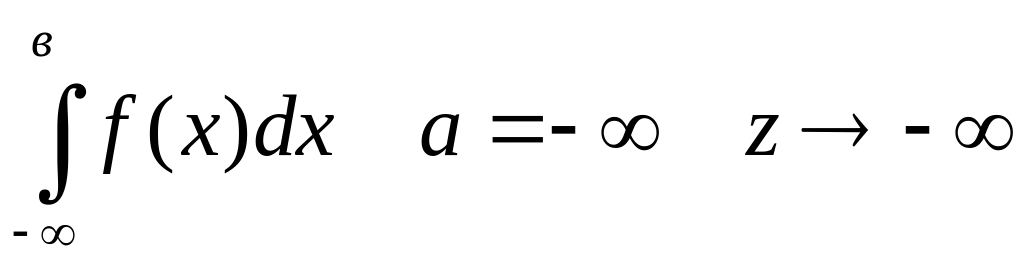
2. Интеграл от неограниченной функции:

, здесь .

df.5 Пусть f(x) определена , что -ют несобственные интегралы , то по df: .

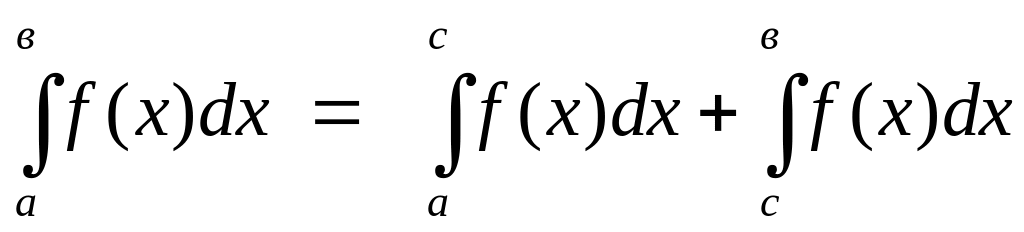
df:

ЗАМЕЧАНИЕ. Можно показать, что в этом определении значение

н. и. не зависит от выбора (^.) ”c”.

Заметим также, что последнее определение эквивалентно следующему определению:

df:

т.е. здесь рассматривается предел функции двух переменных ”y” ”z”. Т.е. при вычислении предела стремятся к независимо.

df.6 f(x) определена на за исключением конечного числа точек и н.и. 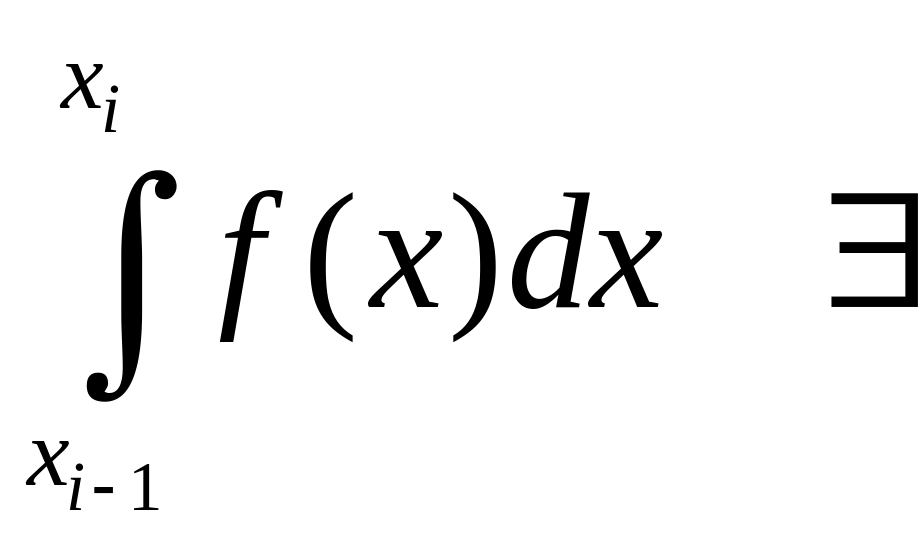-ет (i=1,2,..., n). Тогда н. и. от f(x) на назовем:

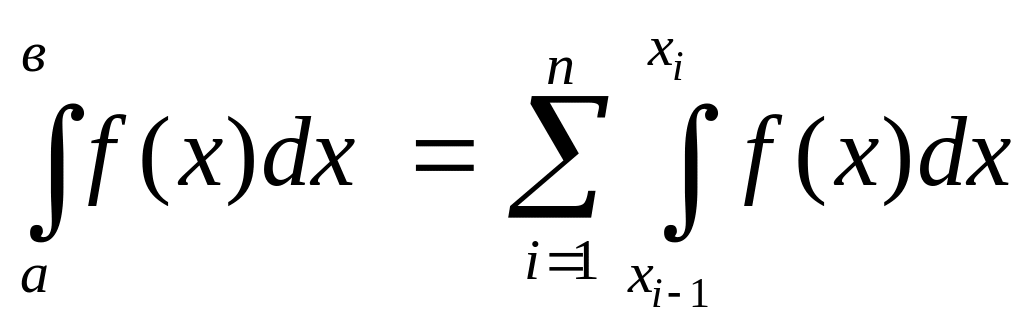df:

По определению полагаем геометрический смысл н. и. – площадь соответствующих «бесконечных» криволинейных трапеций.

y df.3 y df.3

f(x) f(x)–неограни

f(x) ченная вU(в)

0 a x 0 a в x

y y

df.4 df.4

f(x) f(x) – неограни-

f(x) ченная в U(a)

0 в x 0 a’ a в x

y y

df.5 df.5

f(x) f(x) неогра-

f(x) ниченная в

U(а) U(в)

0 x a 0 в x

Если соответствующие пределы в определениях 3, 4 5 -ют и конечны, то говорят, что функция f(x) интегрируема в несобственном смысле ( и т.д.), а интеграл – сходится. В противном случае интеграл – расходится.

Можно показать, что свойства интегралов из df. 3 4 аналогичны, а интегралы вида 5 6 сводятся к ним.

Поэтому в дальнейшем изложении в основном ограничимся несобственными интегралами типа (1), т.е. df. 3