8.3. Задачи в проекциях с числовыми отметками.

Состав геометрических задач, решаемых с применением проекций с числовыми отметками объектов остается традиционным: позиционные и метрические. Здесь рассматриваются те из них, которые являются типовыми в практике строительных работ.

8.3.1. Позиционные задачи. Прямая и плоскость.

На рис.14 показано построение линии пересечения плоскостей  и . Такая задача может встретиться при определении линии пересечения плоских откосов насыпей или выемок. Искомая проекция линии пересечения А₄В₂ плоскостей  и  проходит через точки пересечения двух пар «одноименных» (с одинаковыми отметками) горизонталей заданных плоскостей.

У параллельных плоскостей в проекциях с числовыми отметками:

• параллельны масштабы уклонов;

• равны интервалы;

• отметки возрастают в одну сторону.

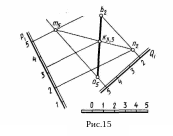
Определение точки пересечения прямой АВ и плоскости Р показано на рис.15. Эта задача решается по тому же плану, что и в ортогональных проекциях. Через заданную прямую АВ проводят вспомо­гательную плоскость Q,, но только не проецирующую, как в ортогональных проекциях, а плоскость общего положения с таким расчетом, чтобы одноименные горизонтали плоскостей Р и Q пересе­кались в пределах чертежа. Затем строят линию MN пересечения плоскостей Р и Q — ее проекция — прямая m₅n₂. Искомая проекция k₃,₃ точки пересечения лежит в месте пересечения проекции данной пря­мой и m₅n₂. Ее отметка определена по масштабу уклона плоскости Р_i.

Плоскость и поверхность .

Линия пересечения плоскости с поверхностью конуса бу­дет проходить через точки пересечения одноименных горизон­талей этих поверхностей Решение этой задачи также встречает­ся в практике строительного проектирования, поскольку откосы насыпей или выемок могут иметь коническую форму. На рис.16 показан пример решения такой задачи. Проекция линии пересечения конической поверхности с плоскостью  проходит через точки А₁, b₂, С₃, D₄

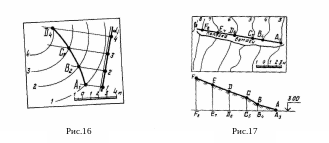
Линия пересечения топографической поверхности с гори­зонтально проецирующей плоскостью  (рис. 17) носит название профиля топографической поверхности Построение этой ли­нии — распространенная в строительном проектировании зада­ча. Для решения ее рекомендуется следующий практический прием. К проекции плоскости , ее горизонтальному следу , прикладывают полоску бумаги, куда переносят точки пересече­ния плоскости с горизонталями топографической поверхности А₃, B₄, С₅, D₆, Е₇, f₈. Полученные точки переносят на горизон­тальную линию — основание профиля, отметку которой задают условно (обычно эта отметка является минимальной). В данном случае отметка основания 3,00 Затем в масштабе чертежа из отмеченных точек откладывают по перпендикуляру вверх пре­вышения отмеченных точек (разность отметки точки и приня­той отметки основания профиля). Искомая линия профиля (се­чения плоскости с топографической поверхностью) будет проходить через точки А, В, С, D, E, F.