Раздел 8. Проекции с числовыми отметками.

8. Проекции с числовыми отметками.

Метод проекций с числовыми отметками получил широкое применение при проектировании сооружений из земли: железных и шоссейных дорог, гидроузлов, каналов, аэродромов, строительных площадок, т.е. в тех случаях, когда высота объекта существенно меньше его длины или ширины.

8.1. Основные понятия. Проекции точки.

Метод проекций с числовыми отметками является частным случаем ортогональных проекций.

Сущность метода заключается в том, что вместо двух ортогональных проекций объекта (на плоскостях П₁ и П₂) изображают одну, чаще всего горизонтальную проекцию, лежащую в плоскости XOY, и рядом с проекцией каждой точки предмета указывают ее отметку (число), определяющую расстояние (обычно в метрах) от точки до плоскости XOY (координата Z). Плоскость XOY называют плоскостью нулевого уровня и обозначают П₀ (рис.1).

При изображении топографической поверхности за такую плоскость принимают поверхность уровня моря. Точки, расположенные на плоскости нулевого уровня, имеют отрицательные отметки и на чертеже проставляются со знаком минус. Точки, принадлежащие плоскости П₀, имеют нулевую отметку (рис.1). Проекция с числовой отметкой является обратимым чертежом, поскольку есть возможность восстановить все три параметра точки, расположенной в пространстве.

Чертежи, выполненные в проекциях с числовыми отметками, принято называть планами, на которых показывают линейный масштаб, необходимый для решения метрических задач (рис.2).

П лан должен быть определенным образом ориентирован относительно сторон света, на

нем в виде стрелки с пометками «С», «Ю» (север, юг) показывают расположение меридиана. Если боковая линия рамки чертежа совпадает с положением меридиана, его можно специально не обозначать.

8.2. Проекции геометрических объектов.

Рассмотрим основные понятия и построения, связанные с изображениями в проекциях с числовыми отметками прямой, плоскости, поверхности.

8.2.1. Проекции прямой.

Для изображения отрезка прямой АВ в проекциях с числовы­ми отметками (рис. 3) показывают проекции двух ее точек А и В.

Длину проекции отрезка А₂В₅ = L называют заложением прямой. Разность расстояний до плоскости П₀ концов отрезка АВ = (h_В - h_А) называют превышением прямой. Отношение пре­вышения прямой к ее заложению называют уклоном прямой: i = (h_В - h_А)/L. Численно уклон равен tg, где a — угол наклона прямой к плоскости П₀. Уклоны выражают в виде простого отношения — 1:1, 1:2 и т.д., в виде процентов — 10%, 20% и т.д. или в виде тысячных — 10%_о, 20%_о и т.д.

Длина заложения отрезка прямой, у которого превышение равно единице длины, называется интервалом прямой. Чтобы получить интервал, нужно заложение прямой разделить на ее превышение, l = L/(h_В - h_А), где l — интервал прямой. Между уклоном прямой и ее интервалом обратная зависимость, т.е. l = 1/ i и i = 1/ l.

И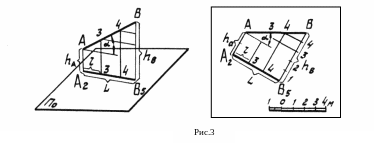 нтервал прямой можно построить графически. Для этого нужно отрезок прямой повернуть вокруг его проекции и совмес­тить его с плоскостью П₀ (см. рис. 3). Из концов проекций отрезка проводят перпендикуляры, на которых в масштабе чертежа откла­дывают расстояния от точек А и В до плоскости П₀, или превыше­ние прямой. Затем на прямой АВ находят точки с целыми отметка­ми, в данном случае точки 3 и 4, и проецируют их на плоскость П₀. Отрезки на проекции прямой (А2-3); (3-4); (4-В5) равны интервалу. Процесс построения на проекции пря-

мой точек, имеющих числовые отметки в виде целых чисел, называют гра­дуированием прямой. Угол a — угол наклона прямой в плоско­сти П₀. АВ — действительная длина отрезка АВ.

По проекциям прямых можно судить об их положении в пространстве относительно плоскости нулевого уровня и других изображенных на чертеже прямых.

Например, все точки прямой АВ имеют отметку 2 – прямая АВ горизонтальная (рис. 4).

Проекция прямой CD — точки cd — пря­мая CD перпендикулярна плоскости нуле­вого уровня (рис. 5).

У параллельных прямых JK и FG (рис. 6) проекции i₂K₄ и f₁g₃ парал­лельны, интервалы равны и отметки возрастают в одном направлении.

Изображенные на рис.7 прямые ML и NP пересекаются, на отметке 4 они имеют общую точку 4. Проекции m₆l₂ и n₃p₅ таких прямых тоже пере­секаются, а точка пересечения проекций имеет отметку 4 как на одной, так и на другой прямой.