Флуктуации при заданной температуре
Используем общую формулу для гауссовых флуктуаций (5.60) и будем считать, что флуктуации температуры отсутствуют. Такая ситуация возникает, например, в растворах, когда устанавливается равновесие по отношению к обмену энергией между растворённым веществом и растворителем. При этих условиях имеем следующую флуктуационную функцию распределения:
.
(5.85)
Эта
формула позволяет вычислить полную
матрицу флуктуаций для всех четырёх
величин
.
(5.86)
Удобно
перейти к переменным
,
тогда оказывается, что
Если же использовать переменные
,
тогда оказывается, что
.
Сначала выберем в качестве независимых переменных N и p. Тогда находим
(5.87)
Для
получения последнего соотношения было
использовано выражение для полного
дифференциала энтальпии
.
Подставляя эти выражения в общее
соотношение (62), обнаруживаем, что
остаются только квадратичные слагаемые:
.
(5.88)
Поэтому
флуктуации давления и числа частиц
статистически независимы, т.е.
,
а среднеквадратичные флуктуации давления
и числа частиц без труда вычисляются:
.
(5.89)
Умножая
дифференциалы (5.87) на
или
на
,
а затем производя усреднения с помощью
(5.52), получаем еще четыре соотношения:
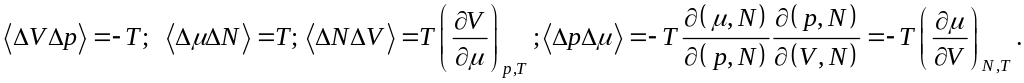(5.90)
Оставшиеся флуктуации удобно вычислять в переменных и V.
Запишем сначала соотношения, аналогичные (5.87):
(5.91)
Здесь использована известная формула:
,
полученная из записи полного дифференциала
.
Подставляя (5.91) в общее соотношение (5.85), находим
(5.92)
Отсюда следует статистическая независимость флуктуаций и , а также следующие две флуктуации:
.
(5.93)
С помощью соотношений (5.91) и (5.93) находим средние от произведений в переменных и V :
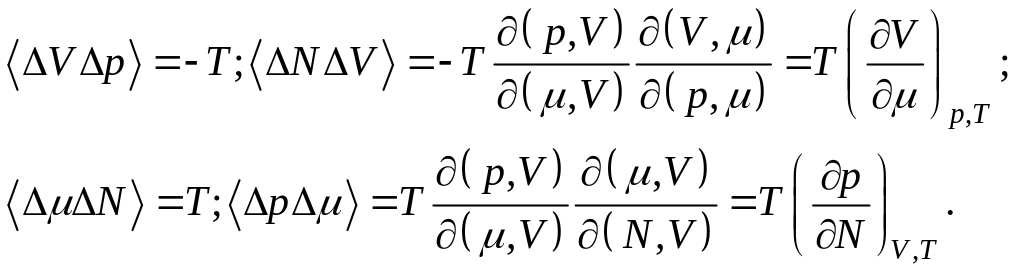(5.94)
Остаётся
доказать, что матрица флуктуаций
симметрична, т.е. средние от произведений
и
в переменных (
)
совпадают с теми же средними в переменных
(
).
Из полученных формул видно, что средние квадраты флуктуаций аддитивных (экстенсивных) величин числа частиц и объёма пропорциональны первой степени числа частиц или объёма. Точно такая же оценка относится к средним значениям от произведения флуктуаций любой пары аддитивных величин. Для таких же величин, как давление и химический потенциал (интенсивные величины) среднеквадратичная флуктуация обратно пропорциональна первой степени объёма или числа частиц. Эта же оценка относится и к среднему значению от произведения флуктуации давления и химического потенциала. Что же касается средних значений от произведения флуктуаций аддитивных и неаддитивных величин, то эти средние имеют порядок единицы (в частности, могут быть равными нулю).
1
.
2
