Флуктуации в обобщённом ансамбле при заданном полном объеме
В этой системе вместо аддитивных величин энтропии и числа частиц используются соответствующие величины, относящиеся к единице объёма. При этом давление следует считать заданной функцией какой-либо пары неаддитивных величин (например, температуры и химического потенциала), в то время как единственной независимой аддитивной величиной является полный объём (V) выделенной системы. Такое описание соответствует гидродинамическому описанию жидкостей и газов. С помощью флуктуационной функции распределения (5.62) произведём вычисления всех элементов матрицы флуктуаций при заданном полном объёме V:
.
(5.77)
Здесь введены обозначения: число частиц в единице объёма, энтропия, отнесённая к единице объёма.
Для
того чтобы вычислить все эти флуктуации,
запишем дифференциалы всех термодинамических
потенциалов, отнесённых к единице
объёма. Начнём с дифференциала энергии
:
Выражение в скобках равно нулю, поскольку
В результате мы имеем первое термодинамическое соотношение:
(5.78)
Второе
термодинамическое соотношение находим
из определения потенциала
(
):
,
или
.
(5.79)
Два
других соотношения
для свободной энергии
и потенциала
,
отнесённых к единице объёма, являются
непосредственным следствием соотношения
(78):
;
.
(5.80)
Полученные
соотношения (5.79) и (5.80) имеют тот же вид,
что и для системы с заданным объёмом,
но с заменой аддитивных (экстенсивных)
величин (
)
на соответствующие неаддитивные
(интенсивные) величины (
).
Учитывая также формальную аналогию
между флуктуационной функцией
распределения (66) и соответствующей
функцией распределения для большого
канонического ансамбля (47), находим все
флуктуации через производные
термодинамических величин, отнесённых
к единице объёма.
Выбирая
в качестве независимых переменных
и
T,
c
помощью соотношений, аналогичных (5.48)
и (5.49), обнаруживаем, что флуктуации
и
статистически независимы, т.е
,
а среднеквадратичные флуктуации
температуры и
без
труда вычисляются:
.
Здесь
и ниже
теплоёмкость на единицу объёма.
Умножая
дифференциалы (46) на
а
затем производя усреднения с помощью
(5.48), получаем еще четыре соотношения:
(5.81)
Оставшиеся
флуктуации удобно вычислять в переменных
и
.
Сначала с помощью соотношений, аналогичных
(5.52)
(5.53), устанавливаем статистическую
независимость флуктуаций
и
а
затем вычисляем среднеквадратичные
флуктуации:
.
(5.82)
Здесь
и ниже
теплоёмкость на единицу объёма.
С помощью соотношений, аналогичных (5.52) и (5.54), находим средние от произведений в переменных и :
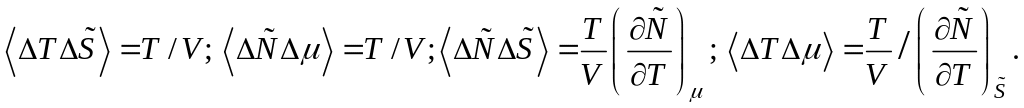(5.83)
Флуктуации термодинамических потенциалов, отнесённых к единице объёма, определяем с помощью соответствующих дифференциалов (5.80). Используя независимость флуктуаций и , сразу находим флуктуацию свободной энергии:
Флуктуацию потенциала, отнесённого к единице объёма, находим, используя независимость флуктуаций и :
Используя
явные выражения для флуктуаций температуры
и
а
также преобразуя производную энтропии
по объёму, находим флуктуацию энергии
(
)
и давления:
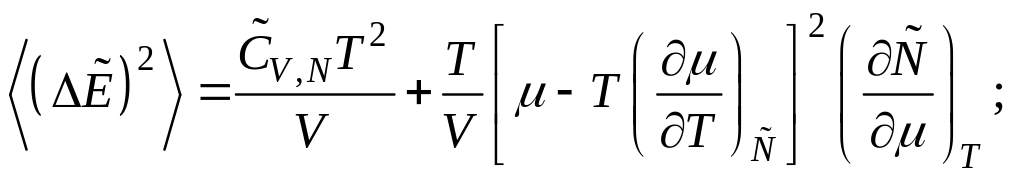
(5.84)
Итак,
все термодинамические потенциалы,
отнесённые к единице объёма, являющиеся
неаддитивными (интенсивными) величинами,
имеют весьма малую среднеквадратичную
флуктуацию
.
Та же самая оценка относится и к средним
от произведения любой пары неаддитивных
(интенсивных) величин
и
.
Что же касается объёма, занимаемого
системой, то его флуктуации имеют
макроскопический порядок
.