2. Флуктуации в обобщённом ансамбле при заданном полном числе частиц

В этой системе вместо аддитивных величин  энтропии и объёма  используются величины, относящиеся к одной частице. При этом химический потенциал следует считать заданной функцией какой-либо пары неаддитивных величин (например, температуры и давления), в то время как единственной независимой аддитивной величиной является полное число частиц N. Такое описание соответствует так называемому твердотельному описанию кристаллического твёрдого тела, когда все величины вычисляются для одной элементарной ячейки. При этом полное число ячеек задаётся независимым образом. Все термодинамические потенциалы, отнесённые к одной частице, выражаются через четыре выбранные неаддитивные величины s, T, v , p. Используя функцию распределения (5.62), произведём вычисления всех элементов матрицы флуктуаций:

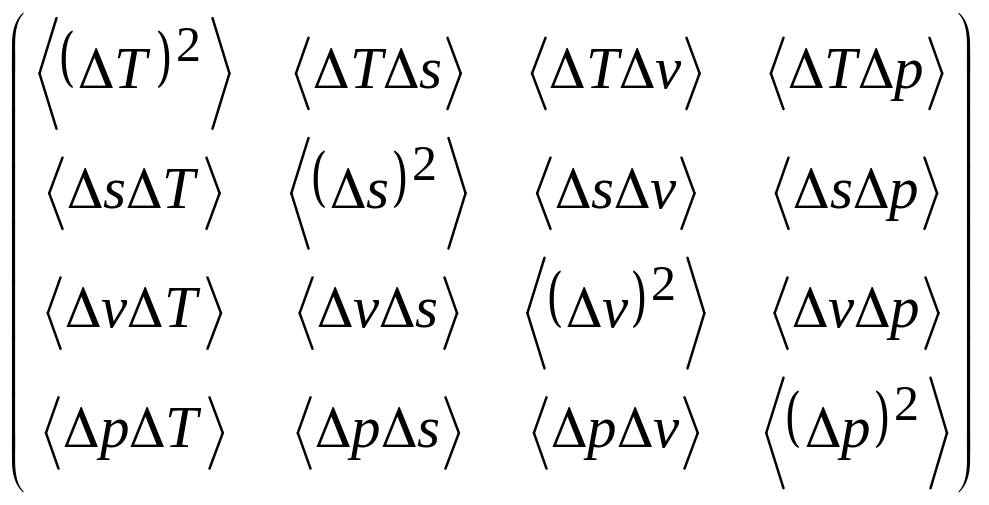. (5.67)

Для того чтобы вычислить все эти флуктуации, запишем дифференциалы всех термодинамических потенциалов, отнесённых к одной частице. Начнём с дифференциала энергии :

Выражение в скобках равно нулю, поскольку термодинамический потенциал равен произведению химического потенциала на число частиц. В результате мы имеем два термодинамических соотношения:

. (5.68)

Два других соотношения: для свободной энергии и энтальпии , отнесённых к одной частице,  являются непосредственным следствием первой формулы из (5.68):

. (5.69)

Соотношения (5.68) и (5.69) имеют тот же вид, что и для системы с заданным числом частиц, но с заменой аддитивных (экстенсивных) величин (S,V ) на соответствующие неаддитивные(интенсивные) величины (s,v). Учитывая формальную аналогию между флуктуационной функцией распределения (5.62) и соответствующей функцией распределения для pTансамбля, находим все флуктуации через производные термодинамических величин, отнесённых к одной частице.

Сначала выберем в качестве независимых переменных v и T. Оказывается, что флуктуации (T, v) статистически независимы, т.е , а среднеквадратичные флуктуации температуры и объема v могут быть получены из формулы (5.22):

. (5.70)

Умножая дифференциалы s и p сначала на , а затем на , и производя усреднения с помощью (5.70) , получаем еще четыре соотношения:

(5.71)

Оставшиеся флуктуации удобно вычислять в переменных и . С помощью соотношений, аналогичных (5.20), удаётся доказать статистическую независимость флуктуаций и Для оставшихся флуктуаций имеем

. (5.72)

С помощью соотношений, аналогичных (5.24) и (5.26), находим средние от произведений в переменных p и s:

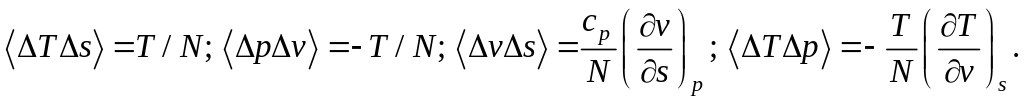(5.73)

Флуктуации термодинамических потенциалов, отнесённых к одной частице, определяем с помощью соответствующих дифференциалов (5.68) и (5.69). Используя независимость флуктуаций и находим флуктуацию свободной энергии:

. (5.74)

Используя независимость флуктуаций и , для флуктуации энтальпии имеем

. (5.75)

Используя явные выражения для флуктуаций температуры и объёма (5.70) и преобразуя производную энтропии по объёму, находим флуктуацию энергии и химического потенциала

(5.76)

Итак, все термодинамические потенциалы, отнесённые к одной частице, являющиеся неаддитивными (интенсивными) величинами, имеют весьма малую среднеквадратичную флуктуацию .

Эта же самая оценка относится и к средним от произведения любой пары неаддитивных (интенсивных) величин и . Что же касается полного числа частиц, то их флуктуации имеют макроскопический порядок .