3. Флуктуации в обобщённом ансамбле. ансамбль

1. Описание обобщённого ансамбля и общая формула флуктуаций

Особенность обобщённого ансамбля состоит в том, что в нём флуктуируют экстенсивные величины (N,V,E), а заданными являются три интенсивных величины (, p, T), между которыми имеется одно термодинамическое соотношение: . Таким образом, нашу систему "удерживают" только две интенсивных (неаддитивных) величины. Это обстоятельство является причиной того, что флуктуации всех трёх величин E, N и V в этом ансамбле, по существу, бесконечны.

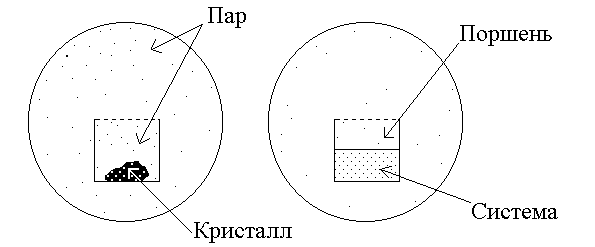
pTансамбль pTансамбль

Рис.2.Обобщенный ансамбль и ансамбль

Для доказательства этих утверждений рассмотрим статистическую сумму обобщённого ансамбля:

(5.54)

Для вычисления среднеквадратичной флуктуации числа частиц произведём интегрирование по энергетическим состояниям, а затем по всевозможным значениям объёма V. В результате получим статистическую сумму pTансамбля , которая выражается через термодинамический потенциал с помощью соотношения .

Следовательно,

. (5.55)

Здесь использовано термодинамическое соотношение , которое приводит к тому, что значения n в пределах имеют одинаковую вероятность. Соответственно этому в пределе находим:

(5.56)

Для нахождения флуктуаций объёма произведём интегрирование по энергетическим состояниям, а затем просуммируем по всевозможным значениям числа частиц. В результате получим большую статистическую сумму которая выражается через потенциал с помощью соотношения . Поэтому

.

Здесь использовано термодинамическое соотношение которое приводит к тому, что значения объёма V в пределах имеют одинаковую вероятность. В пределе находим

. (5.57)

Следовательно, и относительные флуктуации числа частиц, и относительные флуктуации объёма имеют порядок единицы, в то время как нормальная относительная флуктуация должна иметь порядок Далее показано, что флуктуации величины нормальны, так что флуктуации энергии существенно определяются флуктуациями N (т.к. ) и, следовательно, будут также велики.

Рассмотрим флуктуации величин N/V и E/N, для чего воспользуемся общим соотношением:

, (5.58)

где предполагается, что величины  и T связаны уравнением , или

, где (5.59)

По этой причине величину следует считать функцией двух переменных из числа T, p, . Кроме этого, согласно (5.57) и (5.58), она зависит от параметра обрезания N_m или V_m, каждый из которых только множителем отличается от соответствующих средних: или .

Ниже используется вторая возможность, т.е. усреднение по объёму производится в последнюю очередь, так что все усреднённые величины дополнительно зависят от среднего объёма <V>. Несмотря на эти особенности, удаётся записать общую формулу для гауссовых флуктуаций, содержащую три пары дифференциалов:

. (5.60)

Однако при вычислении различного рода флуктуаций необходимо помнить, что

. (5.61)

После подстановки (61) в выражение (60) обнаруживаем, что коэффициент перед обращается в нуль, а флуктуации давления и температуры определяются через производные от энтропии (s) и объёму v, отнесённому к одной частице:

. (5.62)

Ввиду формальной аналогии этой формулы с (5.16) можно заключить, что флуктуации температуры и давления имеют обычную малость ( ), в то время как флуктуации числа частиц имеют негауссовый (степенной) характер.

Аналогично можно исключить из рассмотрения величину полного объёма, если вместо аддитивных величин S и N использовать величины, отнесённые к единице объёма. Для того чтобы получить желаемый результат, запишем следующие, легко проверяемые соотношения:

, .

Далее мы вычислим показатель экспоненты (60):

(5.63)

Можно утверждать, что последнее слагаемое обращается в нуль в силу двух известных соотношений:

, , (5.64)

откуда следует:

. (5.65)

В итоге мы получили функцию распределения типа (43) для флуктуаций энтропии и числа частиц , отнесённых к единице объёма:

. (5.66)

При этом флуктуации объёма имеют степенной характер и макроскопически большую величину.