1. Флуктуации энергии в большом каноническом ансамбле.

В этом ансамбле при заданном химическом потенциале  флуктуирует число частиц. Поэтому сначала запишем определение среднего числа частиц с помощью большой статистической суммы

. (5.33)

Отсюда находим формулу для флуктуации числа частиц:

(5.34)

.

Таким образом, величина числа частиц (34), как и величина флуктуации энергии, пропорциональна числу частиц в первой степени. Флуктуацию энергии при заданном химическом потенциале получаем из тех же соображений, что и при выводе соотношений (32), (33). Формулы для флуктуации числа частиц могут быть получены из соответствующих формул для флуктуации объёма с помощью формального преобразования:

, (5.35)

В результате для флуктуации энергии получим

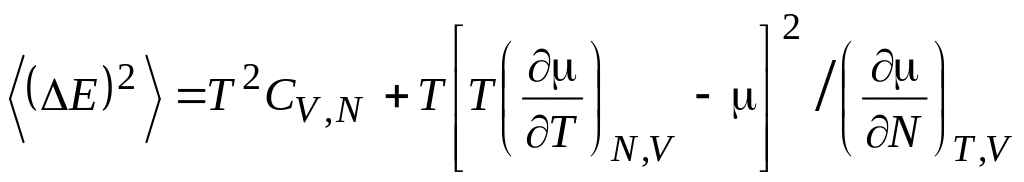. (5.36)

Второй член в правой части (5.36) представляет собой дополнительный вклад во флуктуацию E, возникающий из-за флуктуации числа частиц..

2. Флуктуации в большом каноническом ансамбле.

Произведем суммирование функции распределения большого канонического ансамбля по всем импульсам и координатам выделенной подсистемы для заданного числа частиц n и заданной энергии

Для этой цели умножим функцию распределения на функцию от и просуммируем по всем импульсам и координатам подсистемы:

.

В результате левая сторона является функцией только от энергии и числа частиц подсистемы .

В правой стороне заменим больцмановский фактор на , после чего введем функцию плотности состояний .

Таким образом, имеем:

. (5.37)

Функцию плотности состояний представим в виде производной от полного числа состояний, соответствующих данному числу частиц и энергии, которую, в свою очередь, выражаем через энтропию выделенной подсистемы:

. (5.38)

Последнее соотношение записано в полной аналогии с переходом от плотности состояний к полному числу состояний, когда предполагается, что они несущественно отличаются степенным множителем (по сравнению с экспонентой).

Поэтому, при заданных и T распределение вероятностей и n имеет вид

. (5.39)

Равновесные значения определяются из требования максимальности показателя экспоненты:

. (5.40)

Полагая и и ограничиваясь членами второго порядка по и , получаем

С помощью соотношений (5.40) аргумент экспоненты преобразуется к следующему виду:

. (5.41)

Дальнейшие преобразования произведем с помощью термодинамического соотношения

. (5.42)

Именно здесь используется предположение о том, что термодинамические флуктуации обратной температуры и химического потенциала могут быть определены через дифференциальные соотношения, относящиеся к термодинамически равновесным состояниям. В результате удается найти общую формулу термодинамических флуктуаций, справедливую при заданном объёме:

. (5.43)

Заметим, что это соотношение аналогично формуле (5.16): достаточно произвести замену и .

2. Вычисления флуктуаций при заданном объёме

Общая формула (5.43) позволяет (при заданном объёме) вычислить полную флуктуационную матрицу флуктуаций для всех четырёх величин :

. (5.44)

Удобно перейти к переменным тогда оказывается, что . Если же использовать переменные , имеем .

Сначала выберем в качестве независимых переменных N и T. Тогда

, (5.45)

. (5.46)

Здесь было использовано выражение для полного дифференциала свободной энергии . Подставляя эти выражения в общее соотношение (5.43), обнаруживаем, что остаются только квадратичные слагаемые:

. (5.47)

Таким образом, флуктуации температуры и числа частиц статистически независимы, а среднеквадратичные флуктуации температуры и числа частиц без труда вычисляются:

. (5.48)

Умножая дифференциалы (45) и (46) на и усредняя с помощью (48), получаем еще четыре соотношения:

, , , (5.49)

. (5.50)

Три оставшихся флуктуации удобно вычислять в переменных и S.

Запишем сначала соотношения, аналогичные (5.45) и (5.46):

. (5.51)

Здесь было использовано соотношение .

Подставляя (5.51) в общее соотношение (5.47), находим:

. (5.52)

Отсюда следует статистическая независимость флуктуаций и , а также следующие соотношения:

, , . (5.53)

С помощью соотношений (5.51) и (5.53) находим средние от произведений в переменных и S:

, , ,

.

Остаётся доказать, что матрица флуктуаций симметрична, т.е. средние от произведений и в переменных (T,N) совпадают с теми же средними в переменных (S, ). Из полученных формул видно, средние квадраты флуктуаций аддитивных (экстенсивных) величин  числа частиц, энтропии и энергии пропорциональны первой степени числа объёма Точно такая же оценка относится к средним значениям от произведения флуктуаций любой пары аддитивных величин. Для таких же величин, как температура и химический потенциал (интенсивные величины), среднеквадратичная флуктуация обратно пропорциональна первой степени объёма. Эта же оценка относится и к среднему значению от произведения флуктуации температуры и химического потенциала. Что же касается средних значений от произведения флуктуаций аддитивных и неаддитивных величин, то эти средние имеют порядок единицы (в частности, могут быть равными нулю). Важно заметить, что не только среднеквадратичные флуктуации энергии зависят от того ансамбля, к которому они относятся. Этим же свойством обладает также флуктуация энтропии: при заданном числе частиц она равна , а при заданном объёме  . Однако при этом среднеквадратичная флуктуация температуры равна в обоих случаях.