Лекция 5.

Содержание

1. Фуктуации в p-T  ансамбле при заданном числе частиц

   1. Описание p-T  ансамбля и общая формула флуктуаций

   2. Флуктуации в p-T-ансамбле.

   3. Вычисление флуктуаций при заданном числе частиц.

   4. Флуктуации энергии при заданном числе частиц.

2. Флуктуации энергии в каноническом ансамбле

3. Флуктуации в большом каноническом ансамбле при заданном объеме.

   1. Флуктуации энергии в большом каноническом ансамбле

   2. Флуктуации в большом каноническом ансамбле.

   3. Вычисление флуктуаций при заданном объеме

4. Флуктуации в обобщённом ансамбле. ансамбль

   1. Описание обобщённого ансамбля и общая формула флуктуаций

   2. Флуктуации в обобщённом ансамбле при заданном полном числе частиц

   3. Флуктуации в обобщённом ансамбле при заданном полном объеме

   4. Флуктуации при заданной температуре

Для динамических величин типа энергии, давления или объёма понятие термодинамической флуктуации имеет вполне определённый смысл: достаточно записать соответствующую среднеквадратичную величину, а затем усреднить её по функции распределения выбранного ансамбля: , где угловые скобки обозначают усреднение по соответствующей функции распределения.

Что же касается таких истинно термодинамических величин, как температура и энтропия, то непосредственное вычисление их флуктуаций не представляется возможным. Под флуктуацией энтропии мы будем понимать её флуктуационные изменения, возникающие вследствие того, что в термодинамических соотношениях она является функцией от средних значений всевозможных динамических величин, для каждой из которых понятие термодинамической флуктуации имеет вполне определённый смысл. Точно так же флуктуация температуры может быть определена по той причине, что в термодинамическом равновесии, в силу уравнения состояния, она определяется через средние значения динамических величин  давления, объёма и числа частиц,  для которых термодинамические флуктуации определяются однозначно

1. Флуктуации в p-T-ансамбле при заданном числе частиц.

   1. Описание p-T-ансамбля и общая формула флуктуаций.

Рассмотрим подсистему, которая A) не имеет фиксированного объема, но находится при заданном давлении окружающей среды, B) не является замкнутой, но находится при заданной температуре T, C) имеет фиксированное число частиц N. Предположим, что изучаемая подсистема имеет малый объем и является частью большой замкнутой системы с объемом и энергией . Предположим для наглядности, что термостат, в котором находится наша подсистема, является идеальным газом, имеющим температуру и давление p.

Рис. 1. Наглядное изображение Tpансамбля

При этом вся система  термостат + подсистема  является микроканонической и имеет -образную функцию распределения:

. (5.1)

Здесь импульсы и координаты частиц выделенной подсистемы; импульсы частиц термостата, по которым надлежит произвести интегрирование.

Интегрирование функции удобно произвести с помощью известного соотношения:

. (5.2)

С помощью этого соотношения усреднение по импульсам термостата (термостат можно себе представлять идеальным газом) сводится к вычислению производной от полного числа состояний идеального газа с энергией , который заключен в объеме . Таким образом, функция распределения выделенной подсистемы представляется в следующем виде:

. (5.3)

При заданном числе частиц можно получить явный вид полного числа состояний, а также его производной по энергии для идеального газа:

, (5.4)

. (5.5)

Сравнение (5.5) и (5.4) показывает, что энергетическая плотность состояний отличается от полного числа состояний только множителем пропорциональности , который несущественным образом входит в определение функции распределения (5.3). Поэтому вообще с точностью до нормировочного множителя можно считать, что искомая функция распределения пропорциональна полному числу квантовых состояний:

. (5.6)

Здесь введена функция , которая есть не что иное, как энтропия термостата.

Для получения окончательного выражения разложим энтропию по степеням безразмерного объема и энергии . Используя известные термодинамические определения:

, найдем . (5.7)

Поскольку окончательный результат (5.7) не зависит от физических свойств термостата, можно написать общую квантовомеханическую формулу для для функции распределения ансамбля получим:

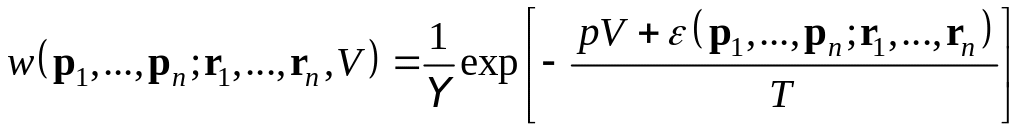. (5.8)

где - уровни энергии при заданном объеме , статистическая сумма распределения:

, (5.9)

Для квантовых систем

, (5.10)

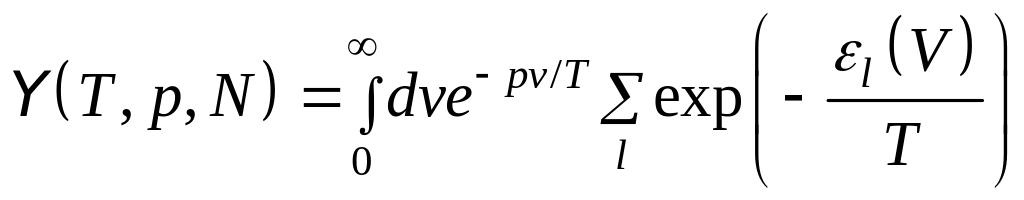. (5.11)

Суммирование в (5.11) происходит по всем уровням энергии системы при заданном объеме .

Через статистическую сумму определяется термодинамический потенциал (в узком смысле) , который зависит от давления и температуры¹:

. (5.12)

2. Флуктуации в 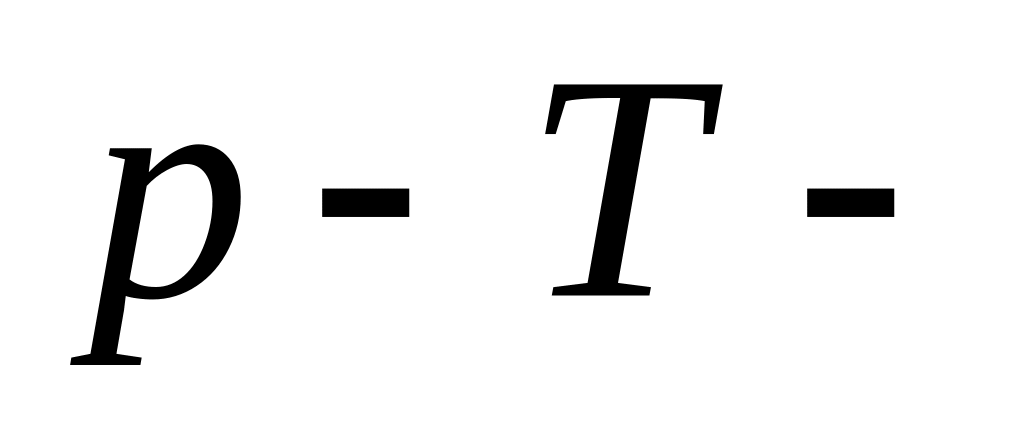ансамбле

Подчеркнем, что в распределениях (5.8) и (5.10) суммирование происходит не по всем различным значениям энергии, а по всем возможным уровням энергии, т .е. по всем возможным состояниям. Поэтому, если мы хотим фиксировать значение энергии, необходимо умножить выражения (5.8) и (5.10) на число состояний при заданном знаяении энергии, т.е. на величину . При этом получим, что

. (5.13)

В выражении (5.13) - вероятность найти состояние с заданной энергией .

Равновесные значения энергии и объема определяются требованием максимальности показателя экспоненты:

. (5.14)

Полагая и и ограничиваясь членами второго порядка по и получаем:

(5.15)

Таким образом, удается получить общую формулу термодинамических флуктуаций:

. (5. 16)

Удобно перейти к переменным T, V, тогда оказывается, тогда

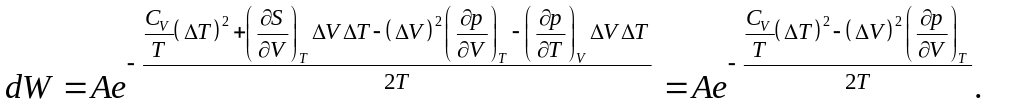
Поскольку , имеем

, . (5.17)

Переменные и независимы. Если же использовать переменные p, S, тогда,

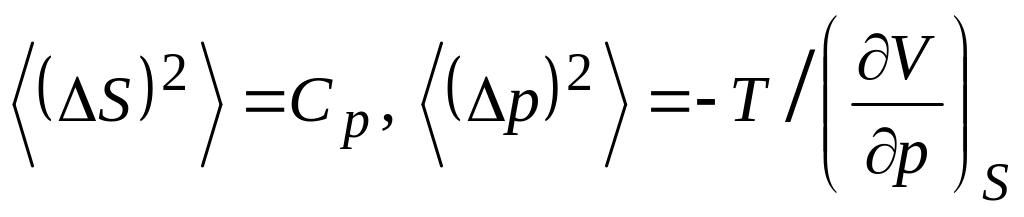, . (5. 18)

Здесь независимыми являются величины и .