Тетрагональная сингония
Необходимым условием отнесения кристаллов к тетрагональной сингонии является наличие одной оси четвертого порядка L4 или зеркально-поворотной оси четвертого порядка L24.
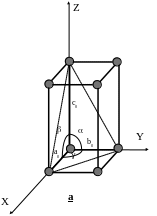
Элементарная ячейка кристаллов тетрагональной сингонии имеет форму параллелепипеда с квадратным сечением (рис. 21). Координатные оси X, Y, Z располагаются под углом 90 друг к другу.
Параметры элементарной ячейки: a0 =b0c0; ===90.
б
Рис. 21. Элементарная ячейка кристаллов тетрагональной сингонии:
а -общий вид; б - вид сверху.
В тетрагональной сингонии выделяется семь классов симметрии:
1. L4 4L2 5P C
2. L4 P C
3. L4 4P
4. L4 4L2
5. L4
6. L24 2L2 2P
7. L24
Простые формы кристаллов тетрагональной сингонии (рис. 22):
1. Тетрагональная пирамида - 4 наклонных грани, сходящихся в одной вершине, через которую проходит L4. Сечение перпендикулярное ей - квадрат.
2. Дитетрагональная пирамида - 8 наклонных граней, образующих тетрагональную пирамиду, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L4 , имеет вид равностороннего 8-угольника с углами, равными через один.
3. Тетрагональная бипирамида - 8 наклонных граней, имеющих форму равнобедренного треугольника и образующих две одинаковые пирамиды, сложенные основаниями.
4. Дитетрагональная бипирамида - 16 наклонных граней, образующих две одинаковые дитетрагональные пирамиды, сложенные основаниями.
5. Тетрагональная призма - 4 вертикальных грани, параллельных L4 и попарно параллельных друг другу, поперечное сечение имеет вид квадрата.
6. Дитетрагональная призма - 8 вертикальных граней, образующих тетрагональную призму, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L4 , имеет вид равностороннего 8-угольника с углами, равными через один.
7. Тетрагональный трапецоэдр - 8 наклонных граней, имеющих форму 4-угольника с двумя равными смежными сторонами. Эта форма похожа на бипирамиду, у которой нижняя часть относительно верхней расположена асимметрично. Эта простая форма не имеет плоскостей и центра симметрии.
8. Тетрагональный тетраэдр - 4 наклонных грани, имеющих форму равнобедренного треугольника. Для этой простой формы характерно наличие зеркально-поворотной оси четвертого порядка L24.
9. Тетрагональный скаленоэдр - 8 наклонных граней, сгруппированных попарно, каждая из которых имеет вид разностороннего треугольника. Две пары нижних граней располагаются симметрично между двумя парами верхних. Для этой простой формы характерно наличие зеркально-поворотной оси четвертого порядка L24.
10. Пинакоид.
11. Моноэдр.
6
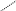
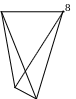
Рис. 22. Простые формы кристаллов тетрагональной сингонии.
Ориентировка кристаллов при проектировании (рис. 23).
С координатными осями X,Y совмещают:
- либо оси L2 (в 1, 4 и 6 классах симметрии);
- либо перпендикуляры к вертикальным плоскостям симметрии (в 3 классе симметрии);
- либо направления, параллельные двум взаимно перпендикулярным ребрам (в 2, 5 и 7 классах симметрии).
С координатной осью Z совмещают оси симметрии L4 или L24.
Единичная грань - грань тетрагональных пирамиды, бипирамиды и тетраэдра.
X
Z
Y
Y
C
X
Y
X
Z
Y
C
X
2)
L4PC
1)
L44L25PC
_
_
_
_
+
+
+
+
_
_
X
Z
Y
Y
X
X
Y
X
Z
Y
4)
L44L2
3)
L44P
_
_
+
+
+
_
_
+
X
Z
Y
Y
X
Y
6)
L24
2L22P
5)
L4
_
_
+
+
X
Z
Y
+
X
+
_
7)
L24
_
+
X
Z
Y
Y
X
Р
+