Средняя категория

К средней категории относятся гексагональная, тетрагональная и тригональная сингонии.

Необходимым условием отнесения кристаллов к средней категории является наличие одной оси высшего порядка соответственно: L₆, L₄, L₃. Вместо L₆ и L₄ могут присутствовать зеркально-поворотные оси шестого и четвертого порядка.

Зеркально-поворотной осью шестого порядка является прямая линия, при вращении вокруг которой на 360 кристалл через 60 трижды совмещается с первоначальным положением и трижды со своим зеркальным отражением (рис. 17 а).

Зеркально-поворотная ось шестого порядка является простой осью третьего порядка, но не наоборот.

О бозначается ось - L₃⁶.

На проекции ось изображается в виде -

Зеркально-поворотной осью четвертого порядка является прямая линия, при вращении вокруг которой на 360 кристалл через 90 дважды совмещается с первоначальным положением и дважды со своим зеркальным отражением (рис. 17 б).

Зеркально-поворотная ось четвертого порядка является простой осью второго порядка, но не наоборот.

О бозначается ось - L₂⁴.

На проекции ось изображается в виде -

L₃⁶

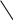
а

Рис. 17. Кристаллы с зеркально поворотной осью симметрии:

а - шестого порядка L₃⁶; б - четвертого порядка L₂⁴.

Гексагональная сингония

Необходимым условием отнесения кристаллов к гексагональной сингонии является наличие одной оси шестого порядка L₆.

Элементарная ячейка кристаллов гексагональной сингонии имеет форму шестигранной призмы (рис. 18). Для удобства пространственной ориентировки кристаллов гексагональной сингонии вводится дополнительная пространственная ось U. Таким образом, выделяется четыре координатных оси X, Y, U, Z. Оси X, Y, U располагаются в горизонтальной плоскости под углом 120.

П

б

араметры элементарной ячейки: a₀=b₀=d₀c₀; ===90; ₁=₂=₃ =120

X

U

Рис. 18. Элементарная ячейка кристаллов гексагональной сингонии: а - общий вид; б - вид сверху;

плоские сетки, параллельные единичным граням: AFB - первого рода (I), AKB - второго рода (II);

в - проекции единичных граней:

п ервого рода - I - (1121); второго рода - II - (1011).

В гексагональной сингонии выделяется пять классов симметрии:

1. L₆6L₂ 7P C

2. L₆ 6L₂

3. L₆ 6P

4. L₆ P C

5. L₆

Простые формы кристаллов гексагональной сингонии (рис. 19):

Различают открытые и закрытые простые формы. Открытые – состоят из граней не полностью ограничивающих пространство и встречаются только в комбинациях с другими простыми формами.

1. Гексагональная пирамида - 6 наклонных граней, сходящихся в одной вершине, через которую проходит L₆. Сечение перпендикулярное ей - правильный шестиугольник.

2. Дигексагональная пирамида - 12 наклонных граней, образующих гексагональную пирамиду, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L₆ , имеет вид равностороннего 12-угольника с углами, равными через один.

3. Гексагональная бипирамида - 12 наклонных граней, имеющих форму равнобедренного треугольника и образующих две одинаковые пирамиды, сложенные основаниями.

4. Дигексагональная бипирамида - 24 наклонных грани, образующих две одинаковые дигексагональные пирамиды, сложенные основаниями.

5. Гексагональная призма - 6 вертикальных граней параллельных L₆ и попарно параллельных друг другу, поперечное сечение имеет вид правильного шестиугольника.

6. Дигексагональная призма - 12 вертикальных граней, образующих гексагональную призму, каждая грань которой разделена на две равные, симметрично расположенные грани. Сечение перпендикулярное L₆ , имеет вид равностороннего 12-угольника с углами, равными через один.

7. Гексагональный трапецоэдр - 12 наклонных граней, имеющих форму 4-угольника с двумя равными смежными сторонами. Эта форма похожа на бипирамиду, у которой нижняя часть относительно верхней расположена асимметрично. Не имеет плоскостей и центра симметрии.

8. Пинакоид - 2 равных параллельных грани, имеющих любую форму. Встречается только в комбинации, например с призмой («основания» призмы).

9. Моноэдр - 1 грань, имеющая любую форму. Встречается только в комбинации, например с пирамидой («основание» пирамиды).

Ориентировка кристаллов при проектировании (рис. 20).

С координатными осями XYU совмещают:

- либо три оси L₂ (1, 2, 6 классы симметрии);

- либо перпендикуляры к плоскостям симметрии (3 класс);

- либо направления, параллельные трем ребрам, расположенным под углом 120 друг к другу (4, 5, 7 классы).

С координатной осью Z совмещают оси симметрии L_6.

Единичная грань - грань гексагональной пирамиды и бипирамиды.

Грани простых форм, принимаемые за единичные, в сложных кристаллах могут быть ориентированы по-разному относительно горизонтальных осей координат. В соответствии с этим различают формы I и II рода.

Е диничная грань формы первого рода пересекает три горизонтальных координатных оси. Единичные отрезки, отсекаемые на осях X и Y равны, а отрезок, отсекаемый на оси U - вдвое меньше. Такая грань проектируется в точку I (см. рис. 18) и имеет символ (1121).

Е диничная грань формы второго рода пересекает две горизонтальные координатные оси и параллельна третьей. Такая грань проектируется в точку II и имеет символ (1011).

В обоих случаях величина единичных отрезков по X, Y, U одинакова.

Величина единичных отрезков по оси Z не равна единичным отрезкам по X, Y и U.

В комбинациях могут встречаться простые формы третьего рода, грани которых проектируются в точку III (см. рис. 18). Такие грани отсекают на всех координатных осях различные по величине отрезки и единичными быть не могут. При наличии в кристалле форм третьего рода отсутствуют оси симметрии L₂ и вертикально расположенные плоскости симметрии (4, 5 и 7 классы симметрии).

1

6

8

Рис. 19. Простые формы кристаллов гексагональной сингонии.

2) L₆6L₂

Z

X

_

+

U

1) L₆6L₂7PC

_

+

Y

Y

С

X

_

+

U

X

_

+

U

3) L₆6P

Y

Z

Y

_

+

_

+

X

U

_

Рис. 20. Стереографические проекции элементов симметрии пяти классов гексагональной сингонии.