1.8 Логарифмические характеристики

Имеем передаточную функцию разомкнутой системы:

Построим ЛАХ и ЛФХ в командном режиме среды MatLab:

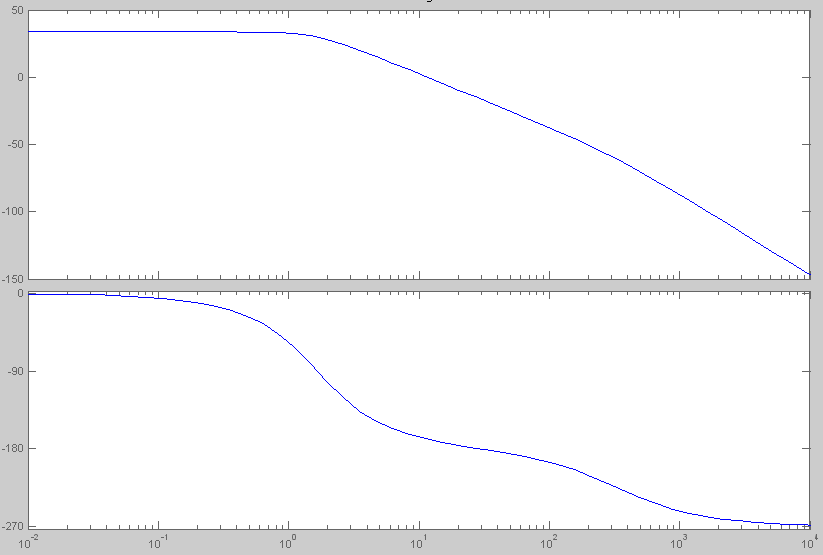
Рис. 1.11 ЛАХ и ЛФХ разомкнутой системы

По полученным ЛАХ и ЛФХ можно судить об устойчивости разомкнутой системы. Разомкнутая система неустойчива, так как ЛФХ достигает значение –180 град при положительных значениях ЛАХ. ЛАХ не удовлетворяет критерию устойчивости Найквиста-Михайлова.

1.9 Корректирующее звено

Для синтеза корректирующего устройства будем использовать среду MatLab 6 и программу AmLAHX 1.1 RC.

Для построения корректирующего звена необходимо построить ЛАХ желаемой разомкнутой системы, параметры быстродействия, параметры качества и устойчивость которой удовлетворяют поставленным требованиям.

Для построения желаемой ЛАХ найдем желаемою частоту среза. Чем больше частота среза желаемой ЛАХ, тем быстрее система реагирует на входное воздействие. К тому же, частота среза должна быть численно меньше, но как можно ближе к значению коэффициента усиления, потому что быстродействие зависит от того, как временные постоянные (характеризующиеся частотой среза) компенсируют «большой» коэффициент усиления.

Итак, выбираем частоту среза:

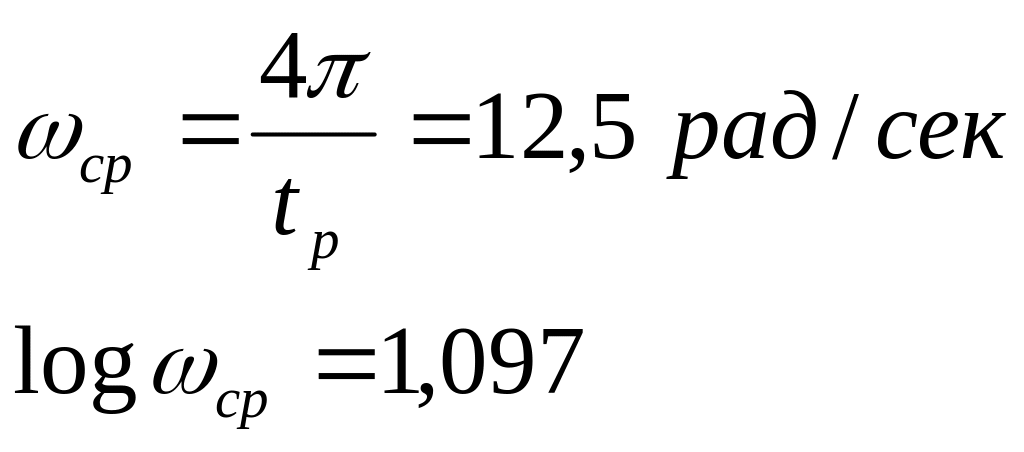
Проводим линию с наклоном , набираем запасы по фазе:

Далее слева проводим линию с наклоном до пересечения с линией, характеризующей коэффициент усиления - линия, проходящая через и имеющая нулевой наклон. Справа повторяем наклон располагаемой л.а.х. - линия с наклоном .

Таким образом, определяем частоты изломов и временные постоянные передаточной функции желаемой системы:

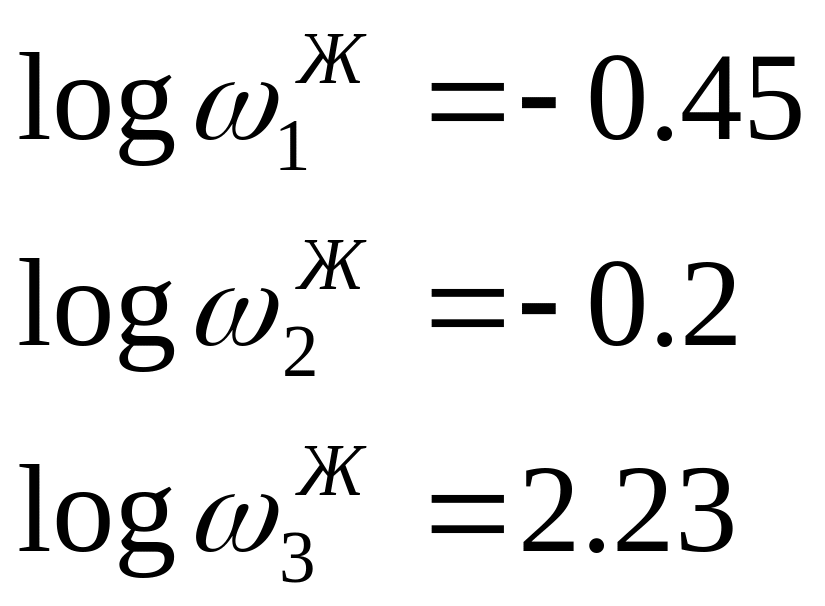
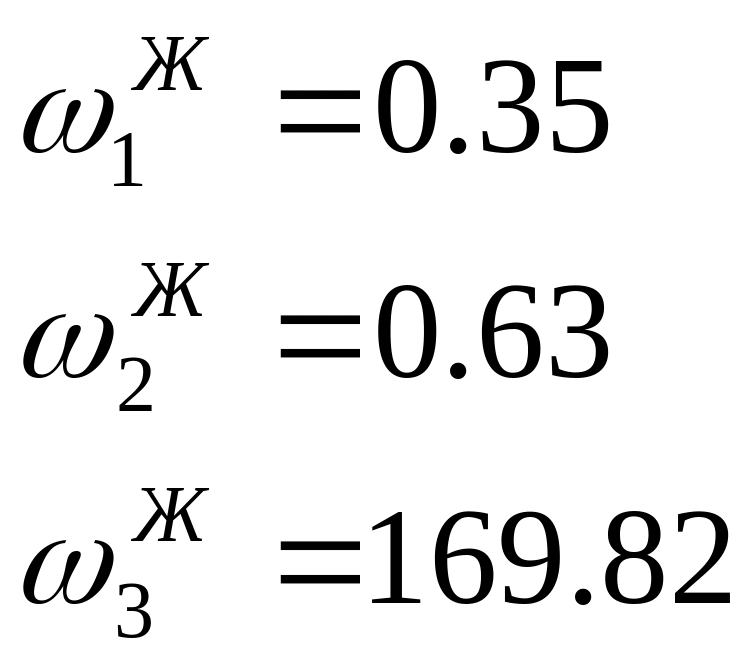
(1.9.1)

Желаемая передаточная функция разомкнутой системы:

, (1.9.3)

где

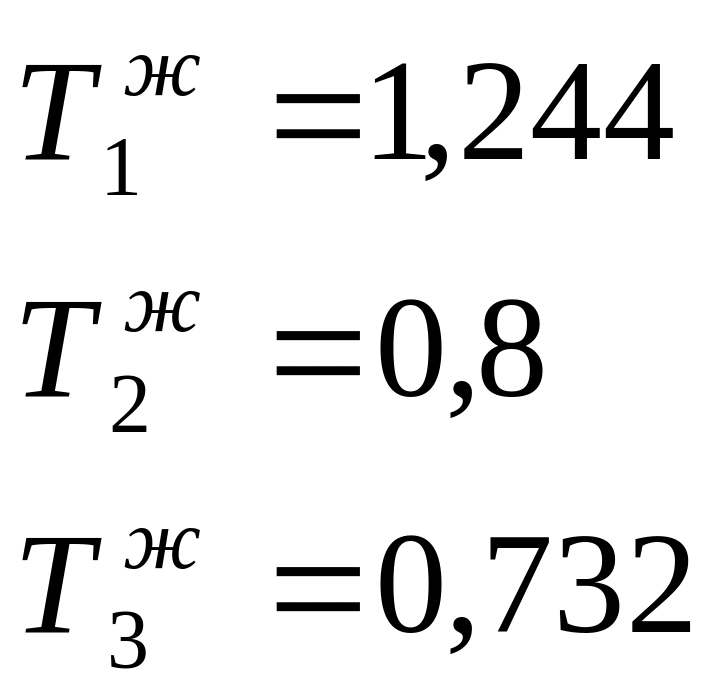
(1.9.4)

1. Запускаем программу AmLAHX в среде MatLab 6.

amlahx(3)

2. Вводим нашу передаточную функцию и желаемые параметры качества системы.

3. Результатом выполнения программы будут ЛАЧХ и передаточная функция корректирующего устройства.

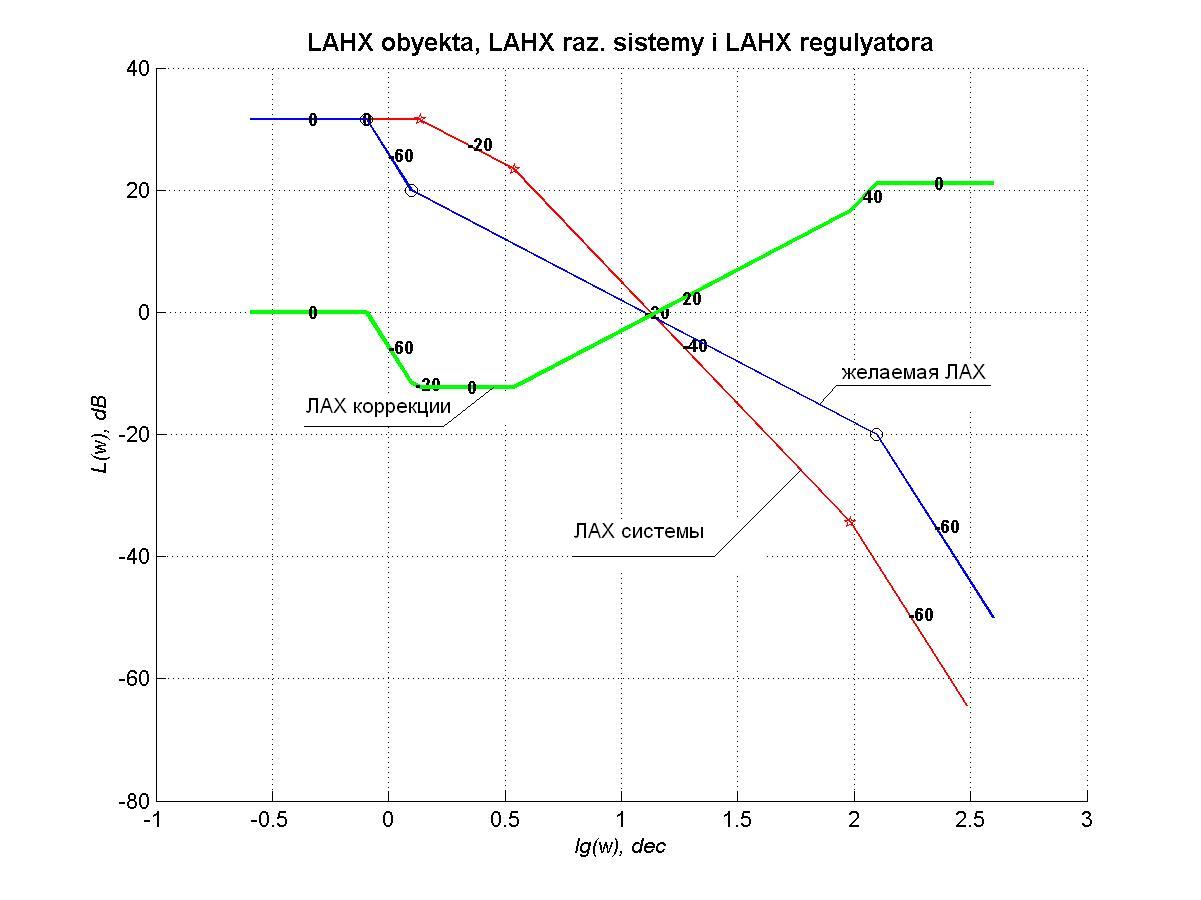
Рис. 1.12 ЛАХ разомкнутой системы, желаемая ЛАХ, ЛАХ коррекции

Построим для нее диаграмму Боде (рис. 1.13):

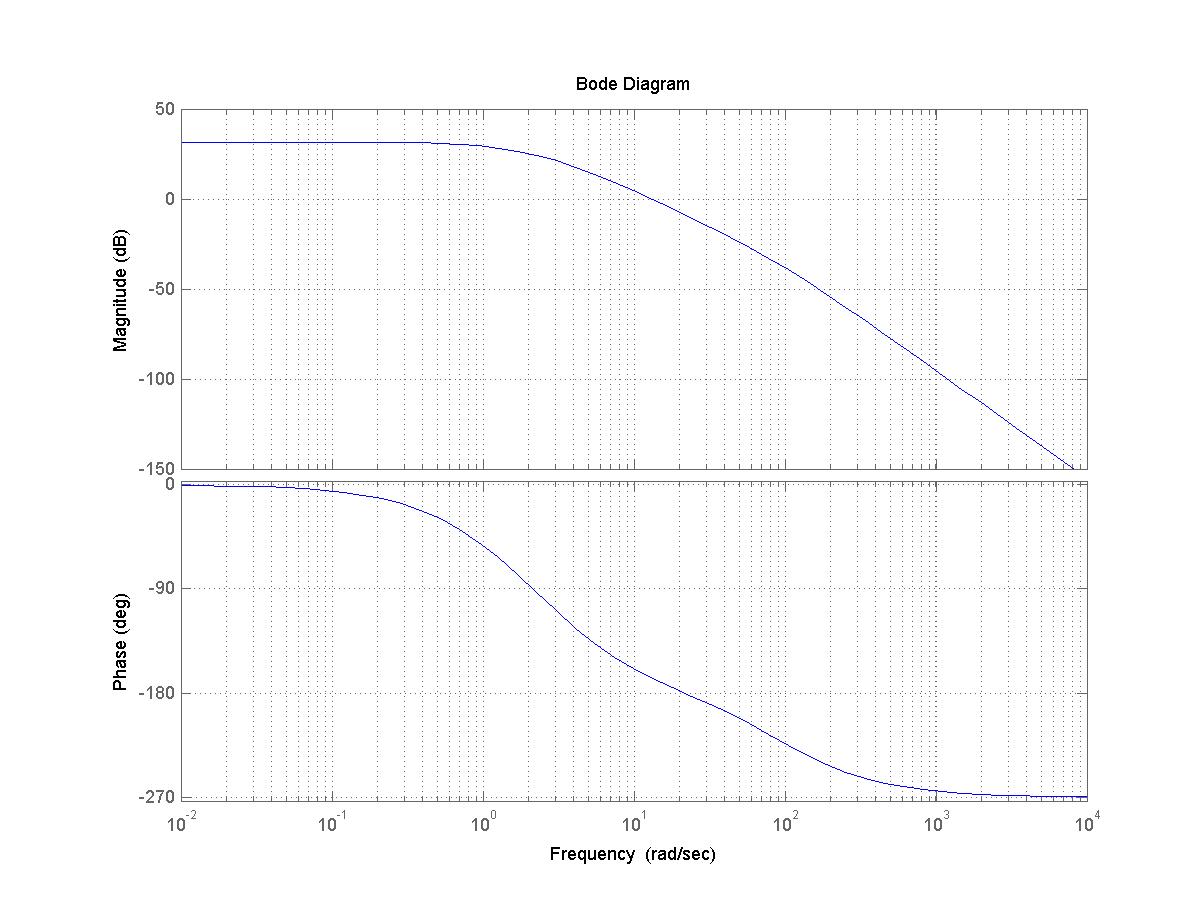
Рис.1.13 Желаемая ЛАХ и ЛФХ

По полученной желаемой ЛАХ строим ЛАХ коррекции и передаточную функцию последовательного корректирующего звена.

Передаточная функция корректирующего звена:

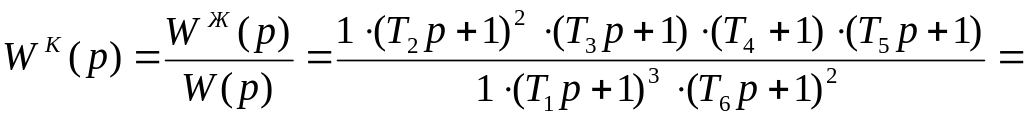
(1.9.5)

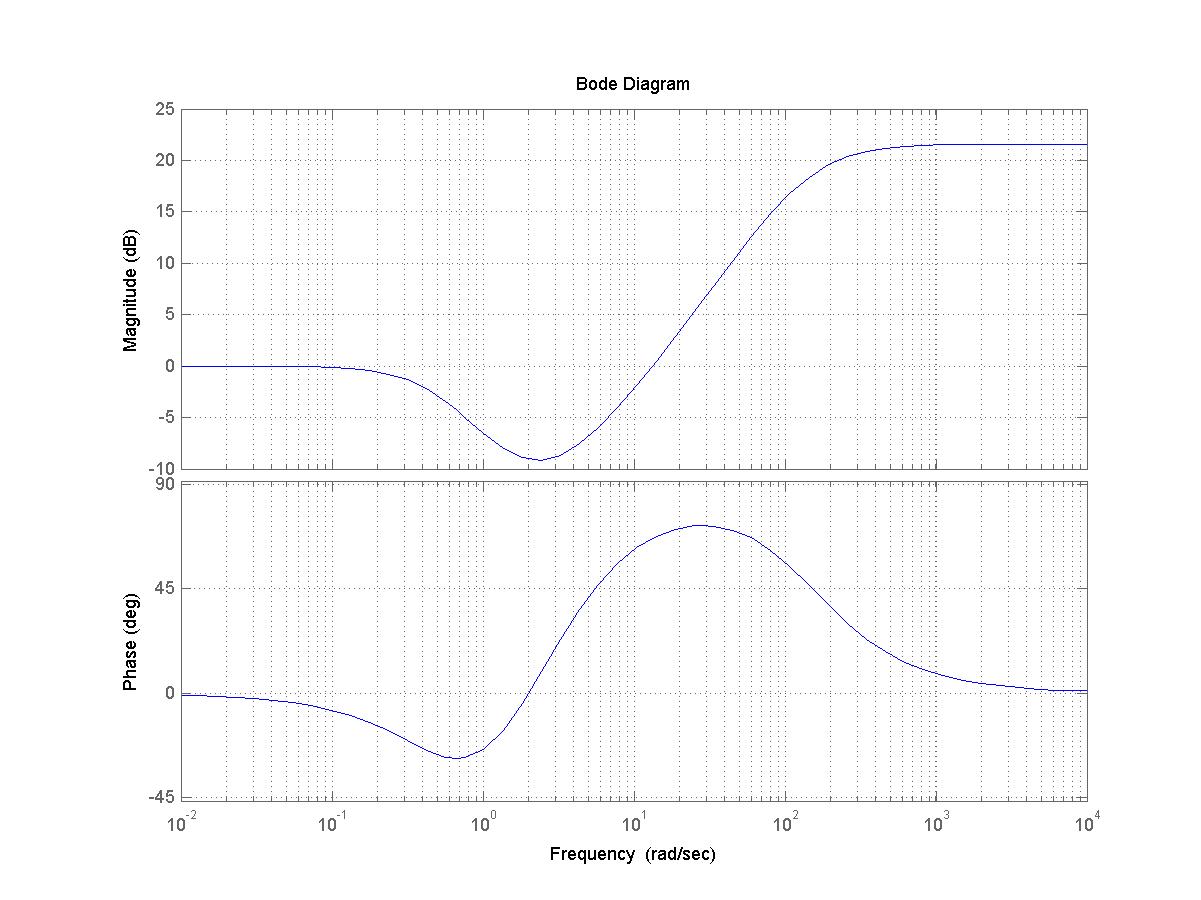
Рис. 1.14 Диаграмма Боде пассивного корректирующего звена

Разбивая передаточную функцию корректирующего звена, получаем 3 дифференцирующих(W1, W2, W3) и 2 интегрирующих (W4,W5) звена:

(1.9.6)

Рассчитаем параметры каждого звена (номиналы конденсаторов берем произвольно)

1) - значит, звено обладает интегрирующим свойством:

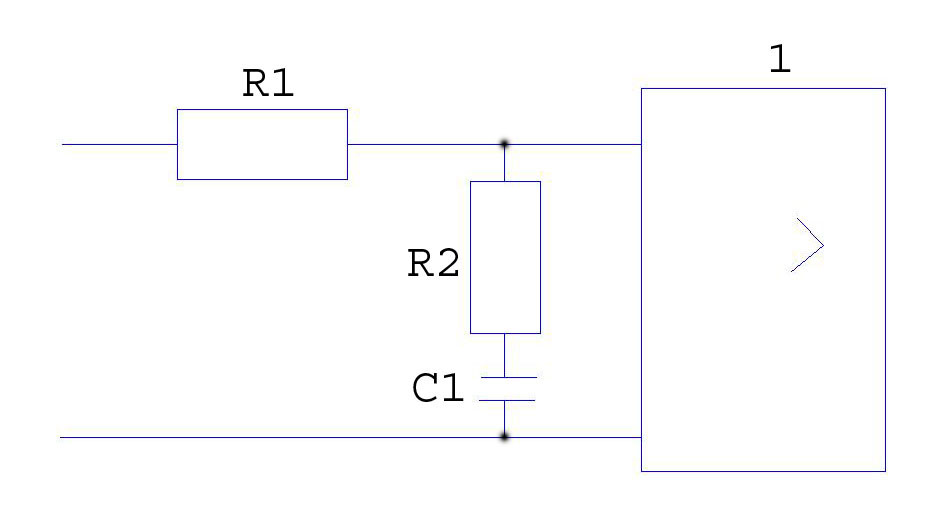
Рис. 1.15 Схема пассивного интегрирующего звена

возьмем , тогда

Так как , то

2) - значит, звено обладает интегрирующим свойством:

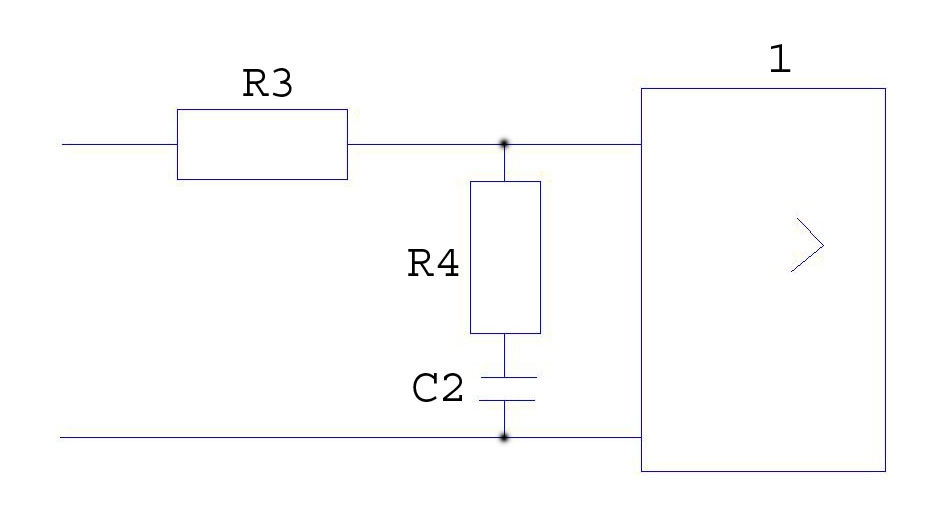
Рис. 1.16 Схема пассивного интегрирующего звена

возьмем , тогда

Так как , то

3) - значит, звено обладает интегрирующим свойством:

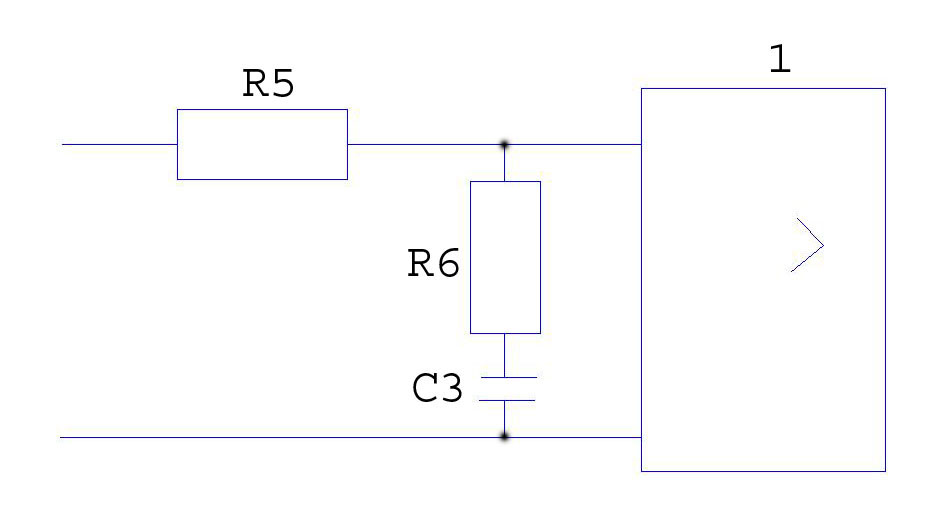
Рис. 1.17 Схема пассивного интегрирующего звена

возьмем , откуда:

4) - следовательно, звено обладает дифференцирующим свойством:

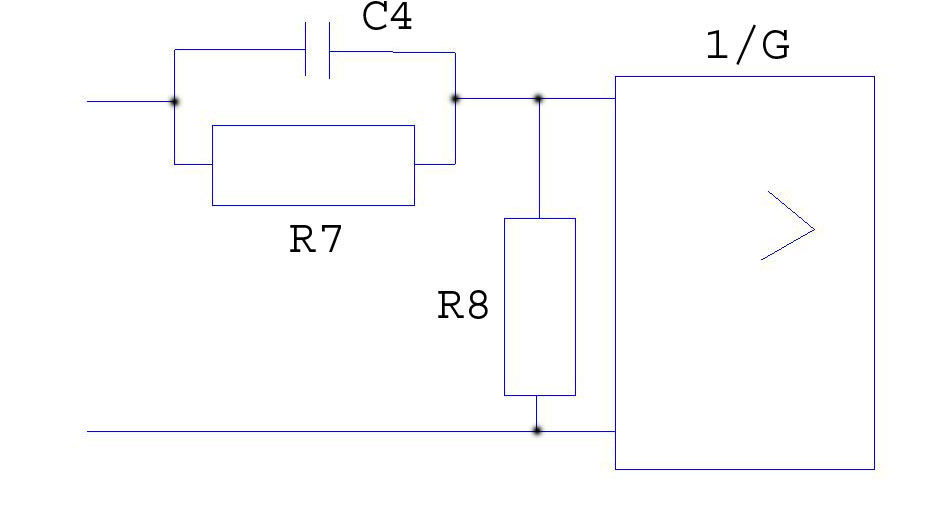
Рис. 1.18 Схема 1-го пассивного дифференцирующего звена

, тогда

5) - дифференцирующее звено

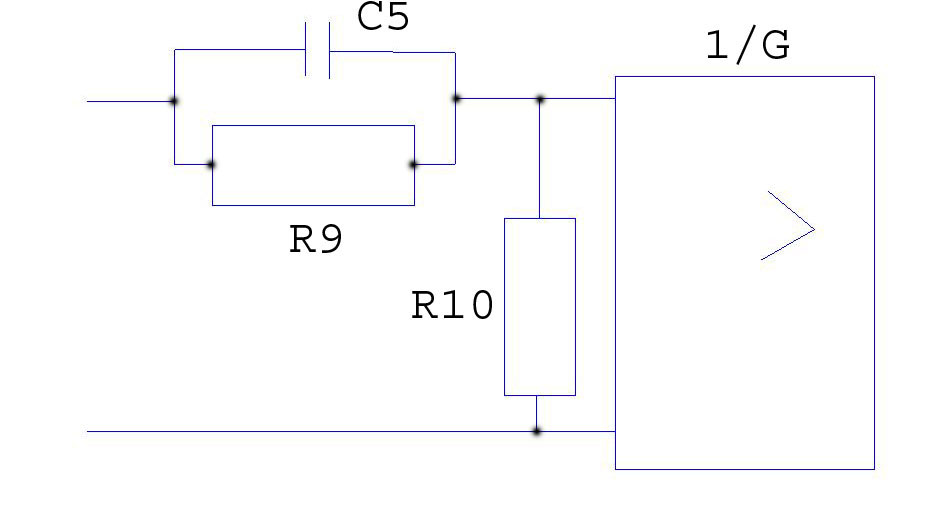
Рис. 1.19 Схема 1-го пассивного дифференцирующего звена

Подставляя наши временные постоянные каждый раз для каждого контура, получаем схему (рис. 1.12)

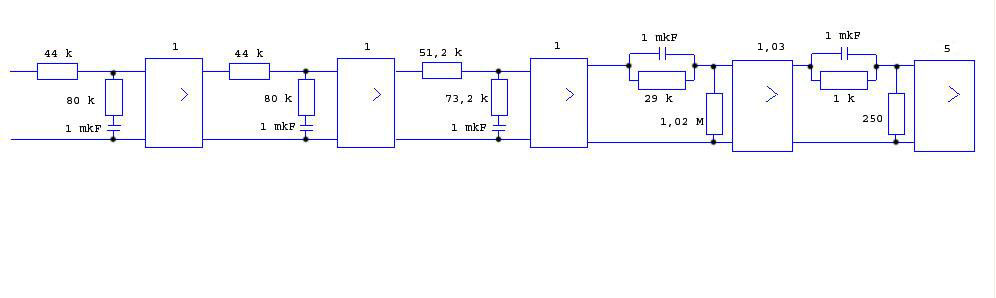
Рисунок 1.20 схемная реализация пассивного корректирующего звена

Таким образом, получившееся корректирующее звено, при включении его в систему, будет повышать качество переходного процесса.

Спроектированное звено предлагается включать в цепь усиления, то есть либо перед электронным усилителем, либо после него, либо непосредственно в электронную схему усилителя.