1.4 Передаточная функция для ошибки
Согласно предыдущему параграфу, ошибка запишется в следующем виде.
Таким образом, найдется передаточная функция для ошибки по команде:
(1.4.1)
И передаточная функция для ошибки по возмущению:
(1.4.2)
1.5 Определение коэффициента усиления системы
Для достижения необходимого параметра качества (в установившемся режиме) – статической ошибки – нужно подобрать соответствующий коэффициент усиления электронного усилителя, а, следовательно, и коэффициент усиления всей системы.
Итак, найдем статическую ошибку.
(1.5.1)
Так как система имеет статизм по отношению к возмущающему воздействию, то для нахождения статической ошибки необходимо использовать входное воздействие – функцию-константу, например:
. (1.5.2)
Итак, получаем изображение по Лапласу:
. (1.5.3)
Теперь находим установившуюся ошибку по формуле (1.5.1):
. (1.5.4)
Отсюда выводим область для необходимого
коэффициента усиления электронного
усилителя, учитывая, что необходимая
ошибка должна быть меньше 2% от величины
входного воздействия. Это обеспечивает
коэффициент усиления:
,
следовательно:
(1.5.5)
Учитывая статическую ошибку, получаем,
что
.
Таким образом, можно выбрать электронный
усилитель так, чтобы выполнялось условие
качества по статической ошибке. Итак,
выбираем электронный усилитель с
коэффициентом усиления
,
те есть берем небольшой запас.
Общий коэффициент усиления разомкнутой системы найдется следующим образом:
.
И коэффициент усиления замкнутой системы:
. (1.5.6)
1.6 Исследование номинальных режимов работы системы
Ставится задача в нахождении такого
управления (величины напряжения на
потенциометре), чтобы напряжение
генератора было
в установившемся режиме.
Допустим, было подано на вход искомое
напряжение
,
тогда, руководствуясь §1.5, можем записать
величину ошибки в установившемся режиме
по формуле (1.5.4):
.
Далее, величину выхода (напряжения
генератора) в установившемся режиме мы
знаем, следовательно, мы знаем, какое
напряжение обратной связи создает эту
ошибку, то есть
.
Теперь можем записать уравнение сумматора для величины входа:
(1.6.1)
Решая уравнение (1.6.1) приходим к следующему:
(1.6.2)
Но для номинального режима работы
системы недостаточно только задать
входное напряжение, так как существует
еще и номинальная нагрузка генератора.
Поэтому ставится задача определить,
как сильно влияет номинальное сопротивление
нагрузки регулируемого и нерегулируемого
генератора
.
Рассмотрим нерегулируемый генератор (система без ООС). Тогда, при отсутствии входного напряжения, изменение регулируемой величины выглядит следующим образом:
(1.6.3)
Формула (1.6.3) в установившемся режиме запишется в виде предела.
(1.6.4)
Таким образом, напряжение будет
уменьшаться на
.
Теперь рассмотрим регулируемый генератор (система охвачена отрицательной обратной связью). В таком случае изменение напряжения запишется в виде:
(1.6.5)
Так, уменьшение будет на
.
Вывод. Регулируемый генератор менее подвержен изменению сопротивления нагрузки, следовательно, регулирование напряжения лучше в системе с обратной связью.
1.7 D-разбиение по общему коэффициенту усиления
Запишем характеристическое уравнение передаточной функции замкнутой системы исходя из характеристического полинома – см. формулу (1.3.4).
(1.7.1)
Коэффициенты в формуле (1.7.1) соответствуют следующим коэффициентам:
Перед тем, как строить D-разбиение, обратимся к критерию Гурвица для определения критического коэффициента усиления.
Составим матрицу Гурвица.
(1.7.2)
Условия Гурвица запишутся в виде:
(1.7.3)
Подставляя коэффициент усиления в (1.7.3) как неизвестную величину, получим систему неравенств.
(1.7.4)
Таким образом, критический коэффициент усиления найдется из (1.7.4):
.
Теперь построим D-разбиение и найдем область устойчивости по общему коэффициенту усиления.
Вещественная и мнимая часть:
(1.7.5)
Годограф рассматриваемого комплексного вектора отображен на рис. 1.3.
Рисунок 1.3. D-разбиение по общему коэффициенту усиления
Рассмотрим интервал
– кандидат на область устойчивости.
Рассмотрим любой коэффициент усиления
из этой области, например
и построим для него годограф Михайлова.
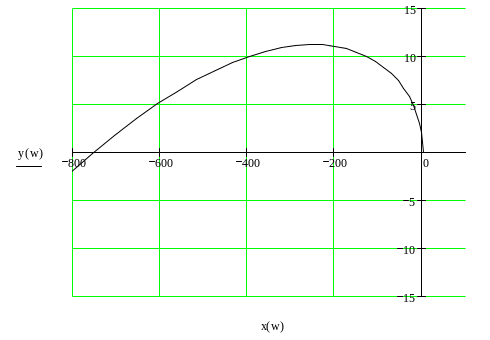
Рисунок 1.4. Годограф Михайлова
Видно, что годограф, изображенный на рис. 1.4 совершает оборот вокруг нуля против часовой стрелки (в положительном направлении), уходя в бесконечность в третьем квадранте, при изменении частоты от нуля до бесконечности. Это свидетельствует об устойчивости разомкнутой системы при коэффициенте усиления из области устойчивости на рис. 1.3.
Таким образом, коэффициент усиления, найденный в §1.5, удовлетворяет условию устойчивости.