2. Основні правила диференціювання функцій

Нехай функції u(x), v(x) мають похідні при деякому значенні x, тобто існують u(x) і v(x). Тоді в точці x мають місце такі правила :

I. Похідна суми функцій дорівнює сумі їх по­хідних:

(u(x) ± v(x)) = u(x) ± v(x).

II. Сталий множник можна виносити за знак похідної

(C·u(x)) = C·u(x) (C = const).

III. Похідна добутку : (u(x)·v(x)) = u(x)·v(x) + v(x)·u(x).

IV. Похідна частки: .

V. Похідна складеної функції. Нехай функція u = (x) диференційовна в точці x, а функція y = f (u) диференційовна в точці u = (x). Тоді складена функція y = f ((x)) диференційовна в точці x, причому

, або ,

тобто похідна складеної функції дорівнює добутку похідної заданої функції по проміжному аргументу на похідну цього аргументу по незалежній змінній.

Таблиця похідних.

(u = u(x), v=v(x), – диференційовні функції від x)

1. ;

2. ;

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

Приклад. Знайти похідні функцій:

1) ; 2) ; 3) ;

4) y = (1 + sin³ 5x)²; 5) ; 6) .

Розв’язання. Використовуючи таблицю похідних, дістанемо:

1)

;

2)

;

3)

;

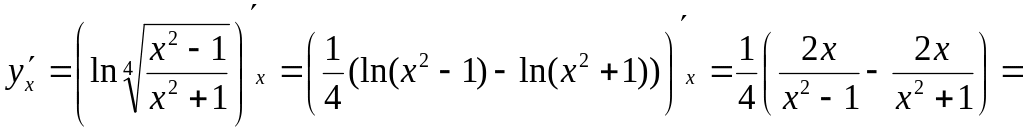
4)

;

5)

;

6)

.

Похідна степенево-показникової функції (формула Лейбніца-Бернуллі).

Степенево-показниковою функцією називають функцію, у якої і основа, і показник є змінні, тобто функцію y(x) = u(x)^v(x), (u(x) > 0).

Для виведення формули її похідної прологарифмуємо обидві частини рівності y = u^v. Маємо: ln |y| = vln u, (u > 0).

Тоді

; ;

; ;

.

Отже, маємо формулу

,

за якою похідна степенево-показникової функції дорівнює сумі по­хід­них: степеневої функції (якщо v(x) вважати сталою) та показникової функції (u(x) вважається сталою).

Об’єднуючи встановлені формули та правила диференціюван­ня, дістанемо таблицю похідних, за допомогою якої і знаходять похідні елементарних функцій.

Диференціювання неявних і параметрично заданих функцій. Рівняння дотичної і до кривої

1. Диференціювання неявно заданих функцій

Нехай функція y = y(x) задана неявно рівнянням F(x, y) = 0. Для знаходження похідної цієї функції потрібно про­диференціювати обидві частини заданого рівняння по x, вважаючи y функцією від x, а потім з одержаної рівності виразити .

Приклад. Знайти , якщо y(x) визначається рівнянням:

1) x² + y² = R²; 2) y = cos (x + y).

Розв’язання. 1) Знайдемо похідну по аргументу x від обох час­тин заданого рівняння. Дістанемо

; 2x + 2y· = 0; x + y· = 0

і виразимо з останньої рівності :

.

2) Аналогічно маємо:

; ;

; ;

; .

З наведених прикладів бачимо, що похідна неявної функції ви­ражається через незалежну змінну і саму функцію. Тому для обчис­лення значення похідної неявної функції при деякому значенні аргу­менту x = x₀ потрібно знати і значення самої функції в точці x₀.