
- •Введение
- •Классификация признаков и показателей в статистике
- •Пример оформления работы
- •Контрольные вопросы
- •Формы и виды статистического наблюдения
- •Пример оформления работы
- •Порядок оформления и защиты лабораторной работы № 7
- •Контрольные вопросы
- •Пример дискретного ряда
- •Пример интервального ряда
- •Пример решения и оформления типовой задачи
- •Данные о стоимости опф и численности работающих на заводах отрасли народного хозяйства
- •Ранжированный ряд по среднесписочной численности работников
- •Ранжированный ряд заводов по стоимости опф с разбивкой по группам
- •Порядок оформления и защиты лабораторной работы № 8
- •Контрольные вопросы
- •Пример решения и оформления типовой задачи
- •Относительные показатели структуры затрат на производство в текущем году, %
- •Относительные показатели динамики
- •Соотношения по видам затрат на производство между заводами в текущем году
- •Контрольные вопросы
- •Пример решения и оформления типовой задачи
- •Контрольные вопросы
- •Контрольные вопросы
- •Пример решения и оформления типовой задачи
- •Данные о заработной плате работников фирмы за текущий период
- •Контрольные вопросы
- •Пример решения и оформления типовой задачи
- •Контрольные вопросы
- •Пример решения и оформления типовой задачи
- •Контрольные вопросы
- •Характер связи в зависимости от коэффициента корреляции
- •Пример решения и оформления типовой задачи
- •Контрольные вопросы
- •Пример решения и оформления типовой задачи
- •Контрольные вопросы
- •Общие индексы средних величин
- •Примеры решения и оформления типовых задач
- •Контрольные вопросы
- •Пример решения и оформления задачи
- •Данные о производстве на предприятиях отрасли в регионе
- •Пример решения и оформления задачи
- •Данные о заработной плате работников предприятия
- •Контрольные вопросы
- •Пример оформления и решения задачи
Контрольные вопросы
Какие ряды называют вариационными?
Какие меры вариации знаете для вариационных рядов?
Назовите формулу для вычисления колеблемости признака?
Назовите формулы для вычисления мер вариации для рядов по несгруппированным данным.
Назовите формулы для вычисления мер вариации для рядов по сгруппированным данным.
Для каких рядов применяют формулы вычисления средней величины изучаемого признака и дисперсии по способу моментов?
Назовите формулу для вычисления средней величины по способу моментов.
Назовите формулу для вычисления дисперсии по способу моментов.
Почему значения дисперсии и среднего значения признака по сгруппированным и несгруппированным данным, вычисленные в лабораторной работе, отличаются?
Что называют условным нулём при расчёте средней и дисперсии по способу моментов?
Чем отличаются формулы для расчёта средних величин стоимости ОПФ и стоимости валовой продукции по сгруппированным данным?
Опишите алгоритм проведения группировки в лабораторной работе.
Опишите правило 3
 .
.Сделайте выводы по результатам выполненной работы.
Лабораторная работа № 9
Тема: Вычисление доверительного интервала для генеральной средней и доли
Цель работы
Приобрести навык расчёта ошибки выборочной средней, границ доверительного интервала по заданной вероятности для средней величины генеральной совокупности и ошибки доли с нахождением границ доли по заданной вероятности с использованием инструментария Microsoft Excel 7.0.
Краткая теория
Определение. Ошибка выборки (репрезентативности) – разница между значением показателя, полученного по выборке и генеральным параметром.
Так,
![]() ,
где
,
где
![]() -
значения средней величины и доли для
генеральной совокупности,
-
значения средней величины и доли для
генеральной совокупности,
![]() -
значения средней величины и доли
выборочной совокупности, отсюда:
-
значения средней величины и доли
выборочной совокупности, отсюда:![]() .
Причём
.
Причём
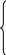
![]() для повторного отбора
для повторного отбора
![]()
![]() для бесповторного отбора
для бесповторного отбора
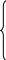
![]() для повторного отбора
для повторного отбора
![]()
![]() для бесповторного отбора
для бесповторного отбора
Значение
параметра t разыскивается по таблице
значений функции Лапласа р=0,997 для
генеральной средней и р=0,954 для генеральной
доли, значение
![]() ,
где m – число единиц совокупности,
обладающих указанным признаком; n –
число единиц или объём выборочной
совокупности.
,
где m – число единиц совокупности,
обладающих указанным признаком; n –
число единиц или объём выборочной
совокупности.
Тогда доверительным
интервалом для генеральной средней
будет:
![]() ;
для генеральной доли, соответственно:
;
для генеральной доли, соответственно:
![]() .
.
Пример решения и оформления типовой задачи
С целью изучения обеспеченности населения города предприятиями общественного питания проведена 5-процентная механическая выборка, в результате которой получено следующее распределение предприятий общепита по числу посадочных мест:
Таблица 9.1
Группы предприятий по числу мест |
Число предприятий |
|
до |
25 |
15 |
25 |
50 |
20 |
50 |
75 |
35 |
75 |
100 |
25 |
100 |
и выше |
5 |
С вероятностью 0,997 определить ошибку выборочной средней и возможные границы, в которых ожидается среднее число посадочных мест на всех предприятиях общепита города.
С вероятностью 0,954 определить предельную ошибку выборочной доли и границы удельного веса предприятий с числом посадочных мест от нижней границы второго интервала до верхней границы четвертого интервала.
|
A = |
62,5 |
h =25 |
Таблица 9.2 |
|
||||||
Группы предприятий по числу мест |
Число предприятий |
Середина интервала |
|
|
|
|
|||||
До |
25 |
15 |
12,5 |
-2 |
-30 |
60 |
|
||||
25 |
50 |
20 |
37,5 |
-1 |
-20 |
20 |
|
||||
50 |
75 |
35 |
62,5 |
0 |
0 |
0 |
|
||||
75 |
100 |
25 |
87,5 |
1 |
25 |
25 |
|
||||
100 |
и выше |
5 |
112,5 |
2 |
10 |
20 |
|
||||
|
|
100 |
312,5 |
|
-15 |
125 |
|
||||
|
|
58,750000 |
|
|
|
|
|||||
|
|
27,69814976 |
|
0,800 |
|
|
|||||
|
|
8,099045083 |
|
0,077974 |
|
|
|||||
50,65095 |
|
66,849045 |
72,203% |
|
87,797%. |
||||||
Для расчёта предельной ошибки выборочной средней t=3, для расчёта предельной ошибки выборочной доли t=2. Так как отбор был бесповторным, то расчёт предельных ошибок производится по соответствующим формулам.
