Задача 3.2.4
З
якою максимальною швидкістю при як
завгодно малій ймовірності спотворення
повідомлень можна передавати інформацію
через біноміальний канал, якщо технічна
швидкість передачі символів
,
а ймовірність помилки при передачі
двійкового символу p
= 0,1; р
= 0,01.
Розв’язання. Для відповіді на поставлене в умовах задачі запитання треба знайти пропускну здатність каналу. Підставивши чисельні значення у вираз (3.22), маємо:
для p = 0,1
для p = 0,01
Аналізуючи отримані результати, можна зробити висновок, що при p = 0,1 із кожної тисячі двійкових символів 531 передають інформацію, а 469 ( майже половина ) використовується для боротьби із завадами. Якщо ж p = 0,01, то для захисту інформації від завад достатньо виділяти 81 символ на 1000 символів, тобто менше 10%.
Задача 3.2.5
Знайти чисельним методом пропускну здатність двійкового стаціонарного несиметричного каналу без пам’яті та без витирання, який має таку матрицю перехідних ймовірностей
-
.
Швидкість
передачі символів
.
Розв’язання. Будемо використовувати вираз (3.11) для пропускної здатності. З урахуванням обмежень умов задачі ентропію Н(Y) можна знайти таким чином:
Для умовної ентропії Н(Y/Х) маємо:
Підставляючи
у наведені вирази значення перехідних
ймовірностей
та надаючи
різні значення, отримаємо дані, що
наведені у таблиці 3.1.
Аналізуючи
дані таблиці 3.1, робимо висновок, що
пропускна здатність дорівнює 0,57787 біт/с
і досягається ( на відміну від симетричного
каналу ) при суттєво неоднаково ймовірних
символах на виході каналу, а саме при
;
.
Проте розподіл ймовірностей
появи символів на вході каналу, який
забезпечує максимальне значення
швидкості передачі інформації, незначно
відрізняється від однаково ймовірного
:
;
.
Таблиця 3.1
|
|
|
|
|
0,4 |
0,516 |
0,9993 |
0,4655 |
0,5338 |
0,45 |
0,5555 |
0,9911 |
0,4334 |
0,5577 |
0,5 |
0,595 |
0,9738 |
0,4014 |
0,5724 |
0,55 |
0,6345 |
0,94715 |
0,36930 |
0,57785 |
0,553 |
0,6369 |
0,94525 |
0,36738 |
0,57787 |
0,6 |
0,674 |
0,9108 |
0,3372 |
0,5736 |
0,65 |
0,7135 |
0,8642 |
0,3052 |
0,559 |
0,7 |
0,753 |
0,8065 |
0,2731 |
0,5334 |
Крім того, навіть значне відхилення від 0,553 незначно знижує швидкість передачі інформації. Якщо ж символи на вході каналу будуть однаково ймовірними, швидкість передачі інформації буде відрізнятись від пропускної здатності лише на
( 0,57787 – 0,5724 ) / 0,57787 · 100 % = 0,9466 %.
Задача 3.2.6
Визначити пропускну здатність двійкового каналу без пам’яті з витиранням, який має таку матрицю перехідних ймовірностей
-
.
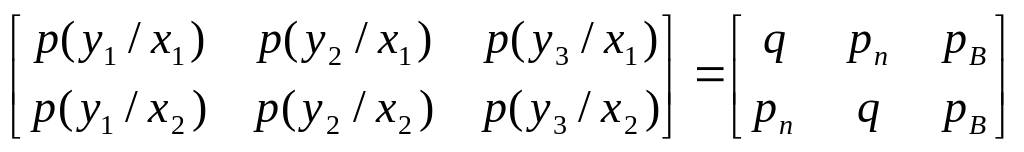Розв’язання.
Канал є симетричним по входу. Це означає,
що умовна ентропія Н(Y/Х)
не залежить від
розподілу
ймовірностей
появи символів на вході каналу. Для
отримання пропускної здатності в цьому
випадку можна скористатися виразом
(3.13), тобто необхідно знайти значення
,
яке максимізує
.
Отримаємо
вирази для ймовірностей
появи символів на виході каналу:
Ймовірність
не залежить від розподілу ймовірностей
появи символів на вході каналу, тому
для максимізації
необхідно, щоб різниця між
та
була якомога меншою ( дивися розділ
1 ). Легко пересвідчитись, що при
Отже
