Хасанов 2003 / шпора

Задача многомерной безусловной оптимизации формулируется в виде:

min f(x),

xX

где x={x⁽¹⁾, x⁽²⁾,…, x⁽ⁿ⁾} – точка в n-мерном пространстве X=IRⁿ, то есть целевая функция f(x)=f(x⁽¹⁾,…,f(x⁽ⁿ⁾) – функция n аргументов.

Т. Необх-ое условие min 1-го порядка

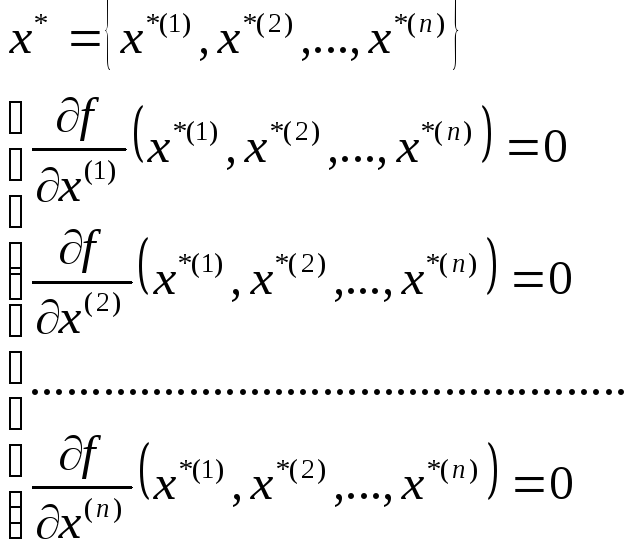стационарная X^*

Т. Необходимое условие 2-го порядка

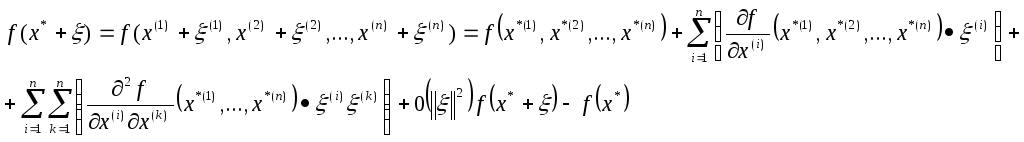
Т. Необходимое условие 2-го порядка

Х^* - стационарная точка

Квадратичная форма записи

Достаточное условие 2-го порядка

Х^* - стационарная точка

необх. условие

Х^* - стацю точка

достат. условие

Х^* - стацю точка

Вычислительные методы нахождения min в многомерном случае

(прямые методы)

первого значения f(x)

1-го порядка f(x), и df/d(x)⁽¹⁾

2-го порядка – f(x), (df/dx)*(x), (d²f/dxdx)(x)

Методы нулевого порядка

усл-е ______: h≤ε

Метод симплекса

Метод деформируемого симплекса

Градиентные методы

Х_к

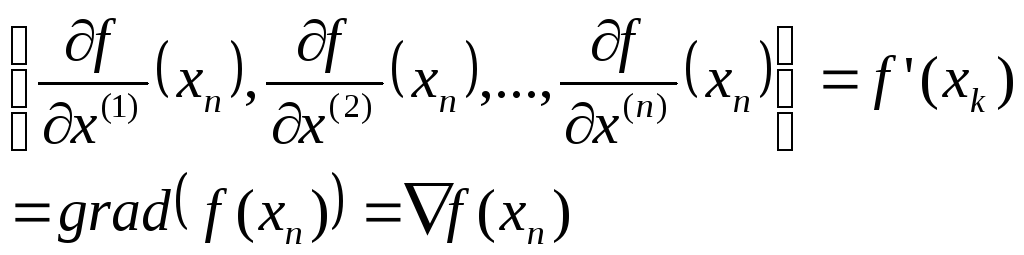
приращение

Общая схема

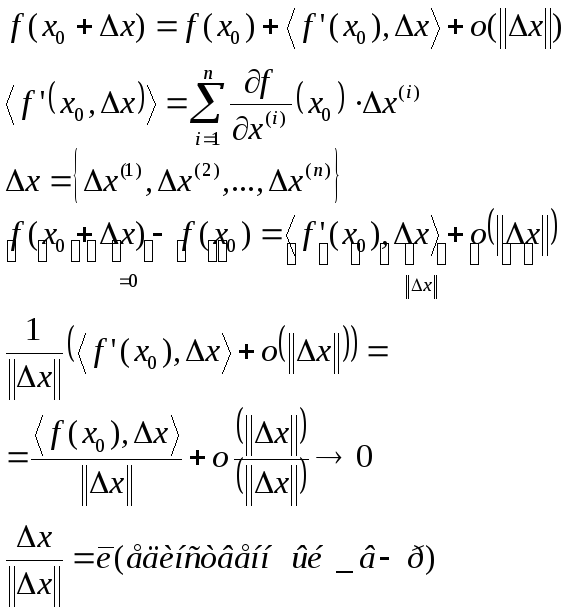
Градиент всегда _|_ линии уровня

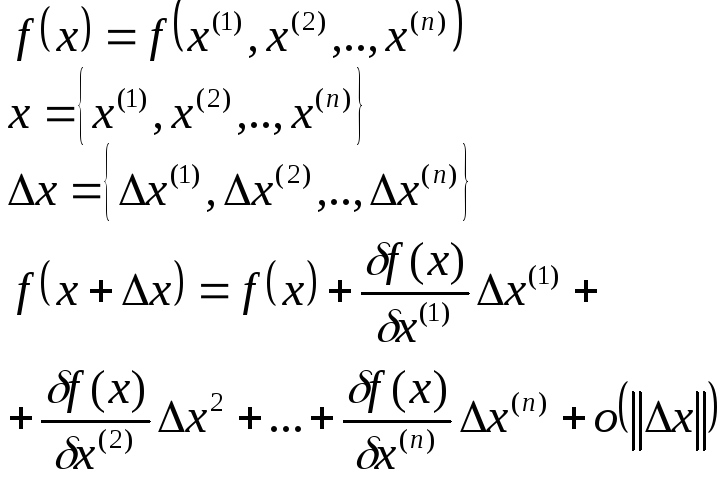
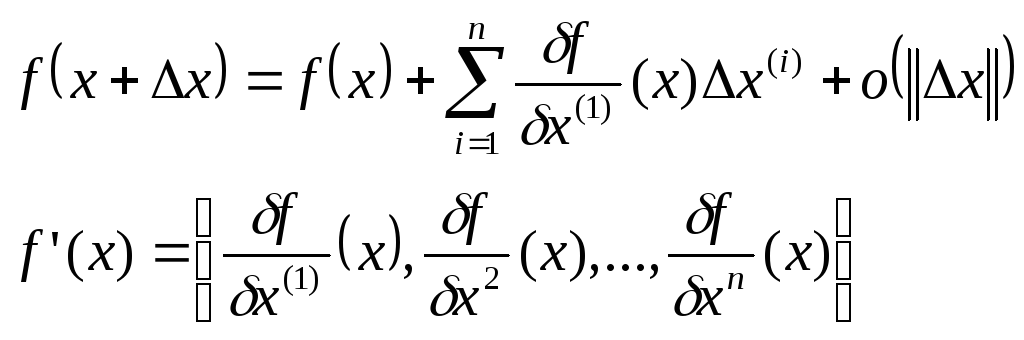
- скаляр. пр-ие

Д-во:

Пусть мы выбрали направ-е (м.б. не совпадающее с напр-ем f ’(x))

Тогда

Нужно найти

Скалярное пр-ие:

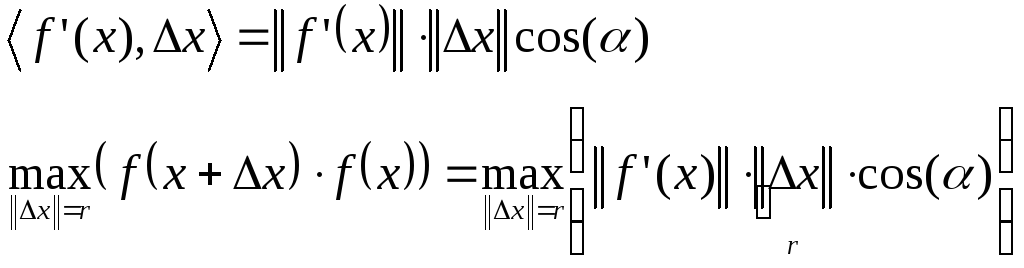
-f ’(x) – антиградиент

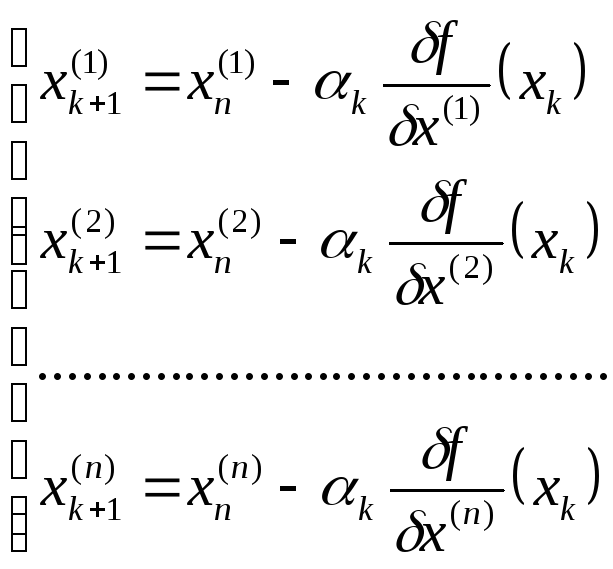
Метод с дроблением шага

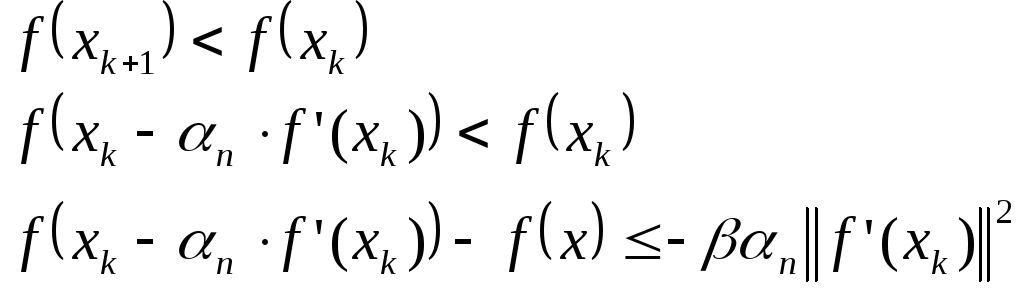
опр-я век-ра

Т. || Если ф-ия f(x) удовл-ет усл-ю для любых 2-х точек (x₁,x₂):

усл-е ___________

то α м. не дробить :

Без доказательства

Метод наискорейшего спуска

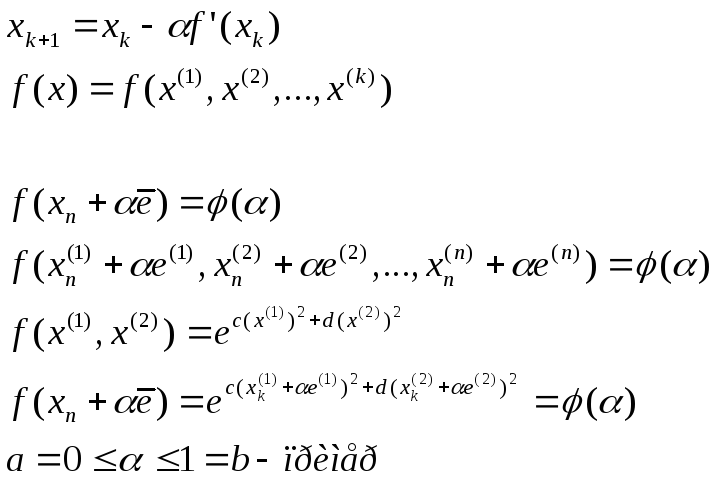
св-во метода:

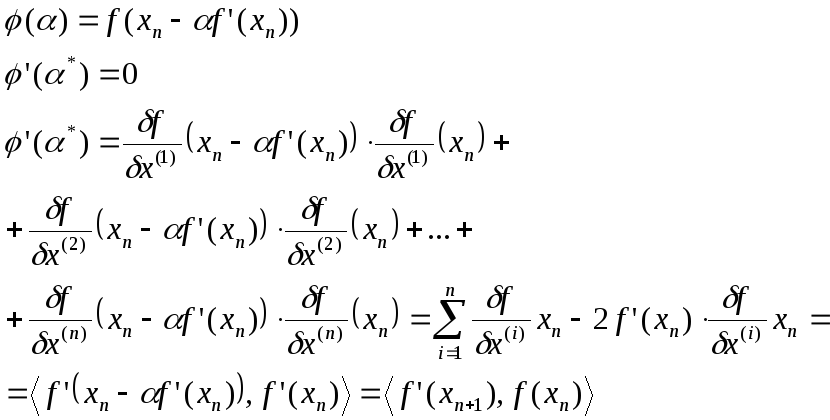
Т. || о сходимости градиентных методов ||

Если f(x) удовл-ет усл-ю Липшица ,

тогда для любого Х₀ обл-т св-вом

Методы покоординатного спуска

замечание: это тоже методы 1-го порядка!

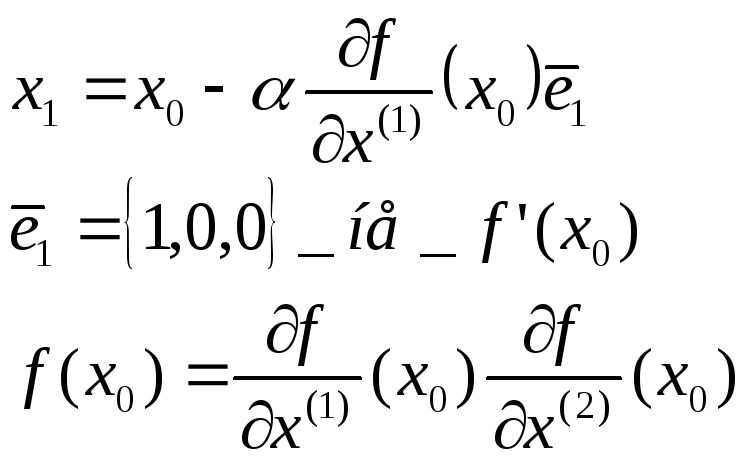
Методы Ньютона(м-ды 2-го порядка)

Общая схема: