1.3. Задача 3. Реализация бих-фильтра на процессоре tms320c50
Задача аппроксимации (конструирование передаточной функции фильтра) в большинстве случаев может быть оптимально решена с использованием общеизвестных программных средств, например, при помощи системы автоматизации математических и научно - технических расчетов MatLab, пакетов для расчета и анализа цифровых фильтров DFDP или FD. При выполнении данной задачи этап аппроксимации реализуется с помощью пакета программ FD.
Для БИХ фильтров предлагается два типа передаточных функций. Передаточные функции, полученные из ФНЧ аналоговых прототипов с помощью билинейного преобразования частоты - это функции Баттерворта, Чебышева I, Чебышева II и Золотарева-Кауэра. Второй тип передаточных функций используется, в основном, для построения амплитудных корректоров.
В результате декомпозиции полученной передаточной функции, которую выполняет программа FD, получается передаточная функция, записанная в виде последовательности передаточных функций первого и второго порядков, т.к. на практике, в основном, используется реализация фильтров в виде каскадного соединения звеньев первого и второго порядка.
Передаточная функция БИХ-фильтра при каскадной форме реализации имеет вид:
|
где множители
соответствуют передаточным функциям
звеньев второго порядка
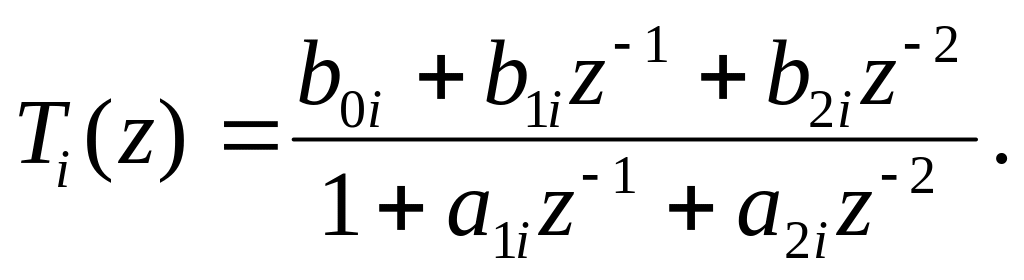
Для реализации звеньев второго порядка могут использоваться различные структуры. На рис. 4 приведены структурные схемы звеньев при различных формах реализации. На этих рисунках не показаны умножители на масштабные коэффициенты, которые должны стоять на входе каждого звена.
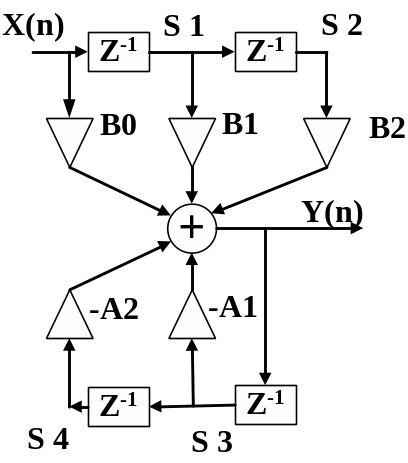
Рис. 4а Схема звена РЦФ второго порядка – прямая форма реализации
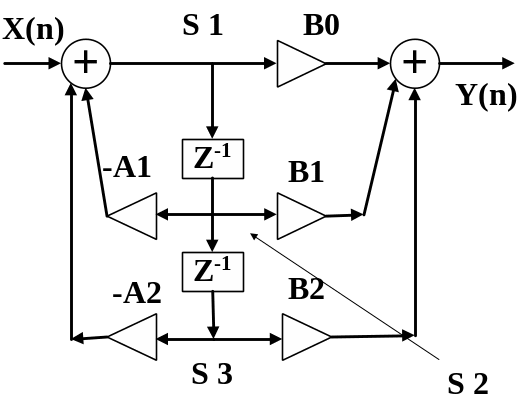
Рис. 4б Схема звена РЦФ второго порядка – каноническая форма реализации
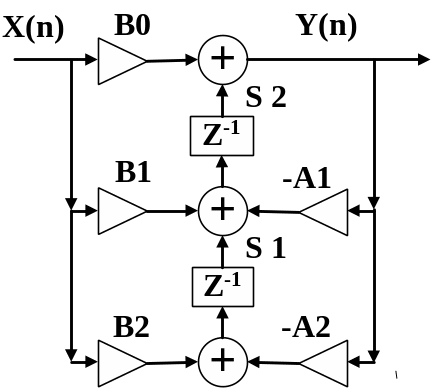
Рис. 4в Схема звена РЦФ второго порядка – трансформированная форма реализации
На рис.4.а приведена прямая форма реализации (структура 1), на рис. 4.б – каноническая форма реализации (структура 2), на рис. 4в – трансформированная форма реализации (структура 3).
Для выполнения задачи необходимо сделать следующее.
1. Написать программу реализации БИХ фильтра в виде последовательного соединения звеньев заданной структуры.
Исходные данные для программы фильтра (коэффициенты и масштабные множители m двух звеньев), которые определяются значением В кода варианта, приведены в табл. 6. Во всех вариантах фильтров используется частота дискретизации 8 кГц.
Структуры звеньев фильтра определяются значением F кода варианта в соответствии с табл. 7. Структурные схемы показаны на рис. 4.
Примеры программной реализации звеньев различной структуры приведены в разделе 4.3.
2. Отладить написанную программу с помощью имитатора процессора.
3. Используя пакет синтеза фильтров FD получить импульсную характеристику для заданного фильтра и составить таблицу её значений.
4. Снять импульсную характеристику полученного фильтра в имитаторе процессора, используя в качестве входного сигнала единичный импульс.
Критерием правильности функционирования программы будет совпадение значений снятой в имитаторе импульсной характеристики с значениями функции, полученной в пакете FD.
5. Определить в имитаторе время вычисления выходного отсчета фильтра (в тактах) и рассчитать максимально возможную частоту дискретизации входного сигнала для данного фильтра.
Варианты заданий отличаются адресами размещения секций программы в памяти процессора и типом прерываний, используемым для ввода входного сигнала.
Значение С номера варианта определяет размещение секций программы в памяти процессора. Адреса размещения секций (в 16-ричной системе) приведены в табл. 2.
Значение D кода варианта определяет тип прерываний, используемый для ввода отсчетов сигнала. Используемые типы прерываний в зависимости от значения D приведены в табл. 3:
INT1, INT2, INT3 – внешние прерывания от устройств, запросы которых подаются на различные входы процессора,
TINT – прерывания по таймеру.
Таблица 6
Значение В |
1 |
2 |
3 |
4 |
5 |
Звено 1 |
b0=0.3845 b1=-0.7691 b2=0.3845 a0=1.0000 a1=0.0388 a2=0.0000 m=0.598
|
b0=0.3525 b1=-.5717 b2=0.3525 a0=1.0000 a1=0.5497 a2=0.2926 m=0.5406 |
b0=0.3149 b1=0.2643 b2=0.3149 a0=1.000 a1=-0.6163 a2=0.6570 m=0.3073 |
b0=0.5074 b1=0.9557 b2=0.5074 a0=1.0000 a1=0.6365 a2=0.6342 m=0.5688 |
b0=0.1986 b1=0.0000 b2=-0.1986 a0=1.0000 a1=-0.5772 a2=0.8451 m=0.3773 |
Звено 2 |
b0=0.3845 b1=-0.3845 b2=0.0000 a0=1.0000 a1=0.1036 a2=0.3346 m=1.0000 |
b0=0.3525 b1=-0.2523 b2=0.3525 a0=1.000 a1=-0.007214 a2=0.8211 m=0.9500 |
b0=0.3149 b1=0.3149 b2=0.00 a0=1.0000 a1=-0.4586 a2=0.000 m=0.9025 |
b0=0.5074 b1=0.5074 b2=0.0000 a0=1.0000 a1=-0.1192 a2=0.0000 m=0.95000 |
b0=0.1986 b1=0.0868 b2=0.1986 a0=1.0000 a1=-0.3071 a2=0.9242 m=0.9500
|
Значение В |
6 |
7 |
8 |
9 |
0 |
Звено 1 |
b0=0.1703 b1=0.0000 b2=-0.1703 a0=1.0000 a1=0.2926 a2=0.8476 m=0.4401 |
b0=0.3245 b1=0.0000 b2=-0.3245 a0=1.0000 a1=-0.2776 a2=0.6399 m=0.5403 |
b0=0.5672 b1=0.1109 b2=0.5672 a0=1.0000 a1=-0.7751 a2=0.5118 m=0.3972 |
b0=0.7056 b1=0.2897 b2=0.7056 a0=1.0000 a1=0.8653 a2=0.6492 m=0.5133 |
b0=0.4419 b1=-0.4633 b2=0.4419 a0=1.0000 a1=0.6610 a2=0.7462 m=0.1660
|
Звено 2 |
b0=0.1703 b1=-0.1666 b2=0.1703 a0=1.0000 a1=0.0070 a2=0.9242 m=0.7737 |
b0=0.3245 b1=0.4918 b2=0.3245 a0=1.0000 a1=0.4167 a2=0.8322 m=0.9500 |
b0=0.5672 b1=0.3834 b2=0.5672 a0=1.0000 a1=1.2385 a2=0.6120 m=1.0000 |
b0=0.7056 b1=0.0885 b2=0.7056 a0=1.0000 a1=-0.4878 a2=0.6152 m=1.00000 |
b0=0.4419 b1=-0.4633 b2=0.4419 a0=1.0000 a1=0.8577 a2=0.4496 m=1.00000
|
.
Таблица. 7
Значение F |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
№ структуры |
1 |
2 |
3 |
3 |
1 |
2 |
2 |
1 |
1 |
3 |
Значение E кода варианта период прерываний (период ввода отсчетов сигнала). Значения периода (в тактах) в зависимости от E приведены в табл. 4.
Методические указания по выполнению задачи и использованию прерываний для ввода сигнала приведены в разделе 3.