8.1 Транспортна задача

Одним із завдань маркетингової політики розподілення є переміщення продукції від постачальника (виробника) до споживача. Якщо продукція є однорідною і зосереджена в декількох пунктах (складах), то план оптимального перевезення визначається за допомогою транспортної задачі.

Транспортна задача (ТЗ) – це специфічна задача лінійного програмування, що застосовується для визначення найекономнішого плану перевезення однорідної продукції від постачальників до споживачів.

Розглянемо постановку ТЗ. У деяких пунктах А₁, А₂, ..., А_і, ..., А_т, що називаються постачальниками, зосереджено товар у кількості відповідно а₁, а₂, ..., а_і, ..., а_т. Пункти В₁, В₂, ..., B_j, …, В_n, що називаються споживачами, мають потребу в цьому товарі в кількості відповідно b₁, b₂, ..., b_j, …, b_n. Числа a_i називатимемо потужностями (пропозиціями) постачальників, a b_j – попитами споживачів. Відома вартість с_ij перевезення одиниці продукції від i-го пункту j-го споживача. Треба скласти такий план перевезень, який дає можливість вивезти всю продукцію, повністю задовольнити потреби споживачів і має мінімальну вартість.

Кількість одиниць продукції, запланованих для перевезення з i-го пункту j-го споживача, позначимо х_ij. Тоді умову задачі можна записати у вигляді наступної таблиці, яку називають матрицею планування(табл.8.1).

Таблиця 8.1

Матриця планування транспортної задачі

Пункти	Споживачі				Запаси
	B1	B2	…	Bn
A1	c11 x11	c12 x12	…	c1n x1n	a1
A2	c21 x21	c22 x22	…	c2n x2n	a2

Продовження табл. 8.1

…	…	…	…	…	…
Am	cm1 xm1	cm2 xm2	…	cmn xmn	am
Потреби	b1	b2	…	bn

Складемо математичну модель задачі.

Оскільки з i-го пункту j-го споживача для перевезення заплановано х_ij одиниць продукції, то вартість перевезення становить с_ij х_ij. Тоді вартість усього перевезення можна подати у вигляді цільової функції

F = c₁₁x₁₁ + c₁₂x₁₂ + … + c_1nx_1n + … + c_m1x_m1 + … + c_mnx_mn. (8.1)

Систему обмежень отримаємо з таких умов задачі:

а) вся продукція повинна бути вивезена, тобто

, (8.2)

б) всі потреби мають бути задоволені, тобто

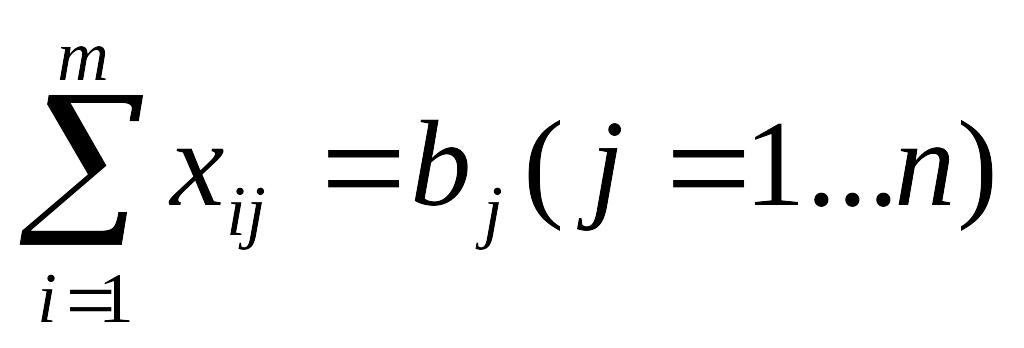. (8.3)

Таким чином, математична модель транспортної задачі набуває такого вигляду: знайти найменше значення лінійної функції (8.1) при обмеженнях (8.2)-(8.3) і при

. (8.4)

ТЗ називається закритою або збалансованою, якщо сумарний попит дорівнює сумарній пропозиції:

= . (8.5)

У противному разі ТЗ називається відкритою або незбалансованою.

Планом ТЗ називають будь-який невід’ємний розв’язок системи обмежень (8.2)-(8.4), який позначають матрицею х = (х_ij) (i = 1…m, j = 1…n).

Оптимальним планом ТЗ називають матрицю х = (х_ij) (i = 1…m, j = 1…n), яка задовольняє системі обмежень (8.2)-(8.4) і для якої функція (8.1) набуває найменшого значення.

Опорний план називається невиродженим, якщо в матриці планування додатних х_ij є m + n – 1, а решта дорівнюють нулю.

Якщо у матриці планування заповнених клітинок менше, як m + n – 1, то опорний план називають виродженим.

Розглянемо маркетингове тлумачення відкритої транспортної задачі.

Нехай сумарний попит перевищує пропозицію, тобто 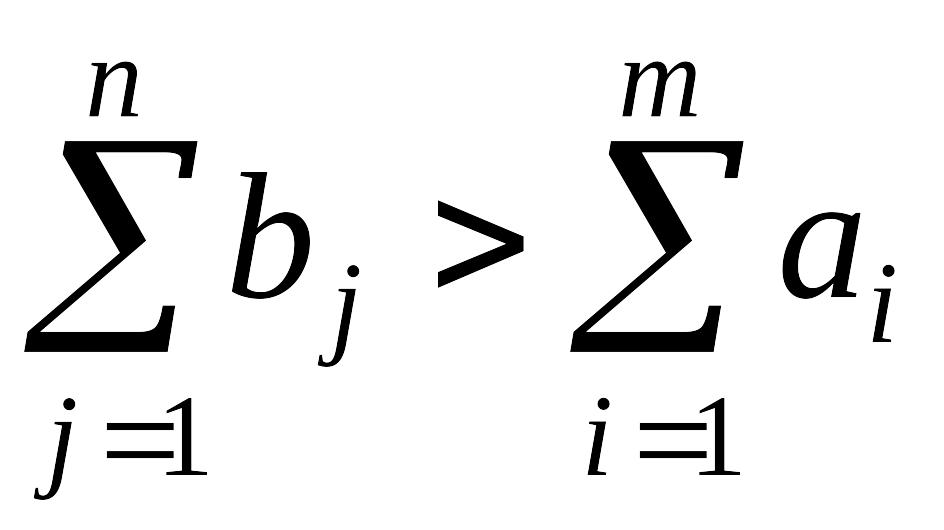. В цьому разі неможливо задовольнити попит усіх споживачів, тому економічна постановка задачі така: скласти план перевезень, за якого весь товар від усіх постачальників вивозиться, попит споживачів по можливості задовольняється (споживачі одержують товари в кількостях, які не перевищують їх попиту) і сумарні транспортні витрати мінімальні.

Розглянемо математичну модель такої задачі.

Увесь товар, який мають постачальники, вивозиться:

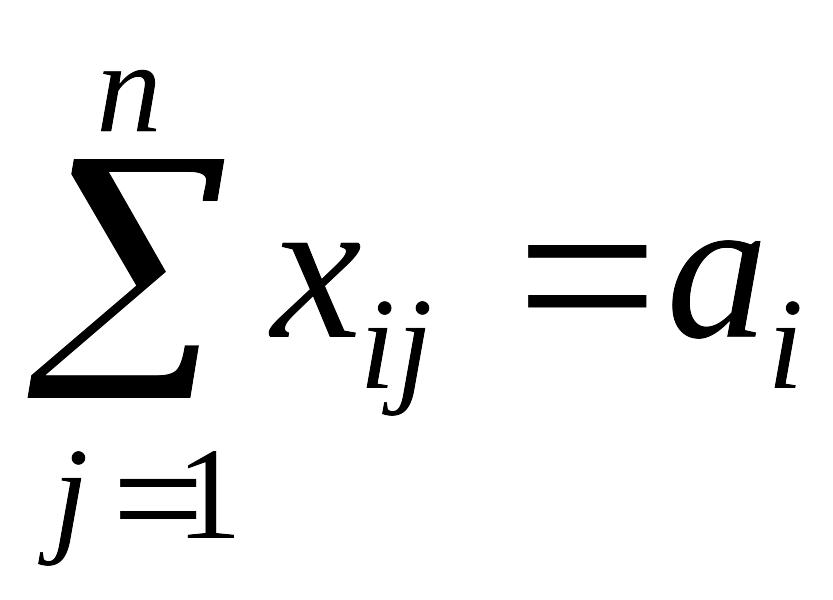
. (8.6)

Споживачі одержують товар у кількостях, які менші або дорівнюють попиту на нього:

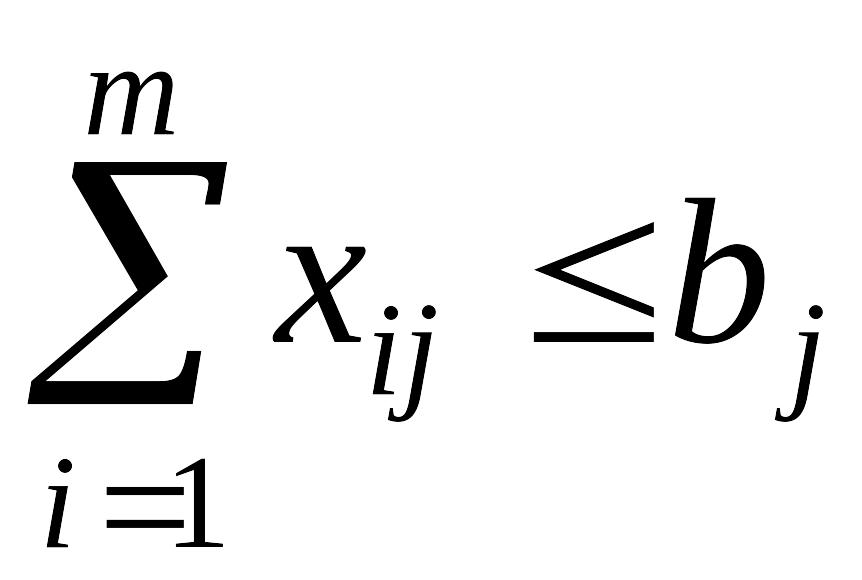
. (8.7)

Умова невід’ємності (8.4) і цільова функція (8.1) не змінюються

Якщо сумарна пропозиція перевищує сумарний попит 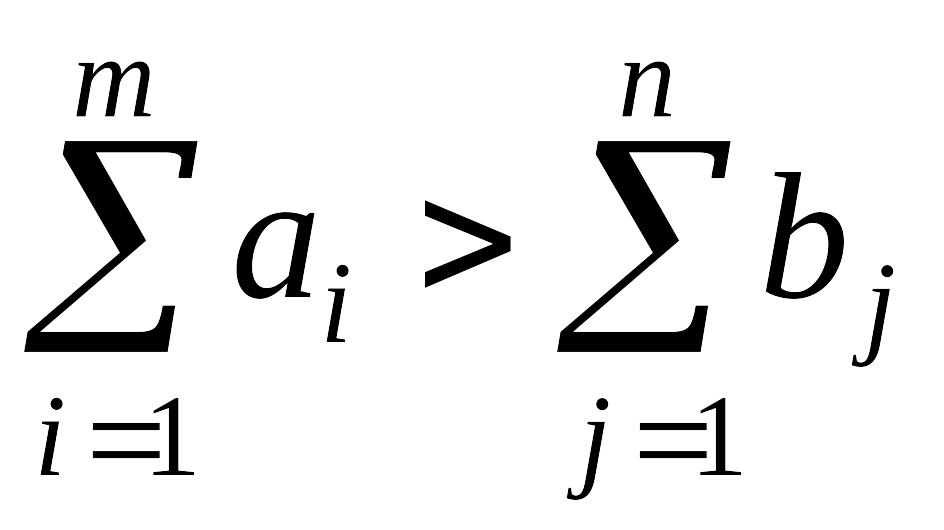, задоволення попиту споживачів не супроводжується повним вивезенням товару від постачальників. Отже, економічна постановка задачі така: скласти план перевезень, за якого потреби всіх споживачі задовольняються, від постачальників вивозяться товари в кількості, яка не перевищує їх потужності, й сумарна вартість перевезень мінімальна.

Першу умову задачі можна записати у вигляді

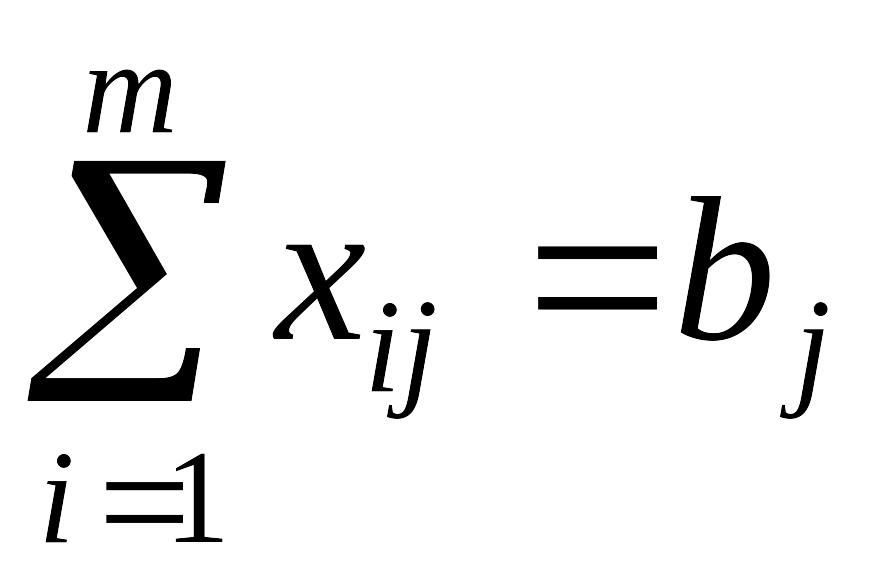; (8.8)

друга умова

. (8.9)

Окрім того, зберігаються умови невід’ємності (8.4) і цільова функція (8.1).