Нелінійні зв'язкові структури
Однозв'язний список завжди лінійний. Двозв'язний список може і не бути лінійним, якщо другий покажчик кожного елемента списку задає порядок довільного виду, який не є зворотним стосовно порядку, встановлюваному першим покажчиком елемента. Кожний елемент такого узагальненого двозв'язного списку міститься одночасно в двох різних однозв'язних списках, як показано на рис. 5.7 [14, 15].
На цьому рисунку змінні S1 і S2 є покажчиками початку двох різних однозв'язних списків, у які одночасно входить кожний із п'яти елементів, а Р1 і Р2- позначення зв'язків у першому і другому однозв'язних списках відповідно. Покажчики S1 і S2 є компонентами двох різних дескрипторів однозв'язних списків.
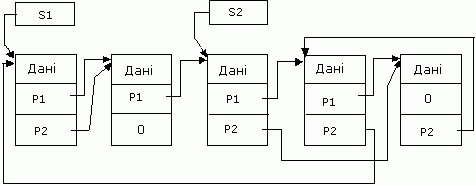
Рис. 5.7 Приклад логічної структури узагальнюючого двозв'язкового списку
У ще більш загальному випадку кожний елемент зв'язкового списку може містити довільне кінцеве число зв'язків , однакове або різне в різних елементах. У результаті такого узагальнення утворюється багатозв'язний список, кожний елемент якого входить одночасно в стільки різних однозв'язних списків, скільки є зв'язків у відповідному елементі. При цьому не обов'язково, щоб кожний елемент неодмінно входив у всі однозв'язні списки. Такий багатозв'язний список як би прошитий в різних напрямках багатьма зв'язками. Тому багатозв'язні списки іноді називаютьпрошитими списками. Використовується також ще одна назва багатозв'язних списків - плекси .
Найбільш загальний вид багатозв'язної структури - багатозв'язна структура , яка характеризується наступними властивостями.
Кожний елемент структури включає довільну кількість однонаправлених зв'язків з другими елементами.
З кожним елементом може зв'язуватися довільна кількість інших елементів.
Кожний зв'язок в структурі має не тільки напрямок , але і вагу.
При обробці багатозв'язних структур важливе місце має процедура виключення вузлів. Існує два основних метода: метод лічильника та метод "збору сміття".
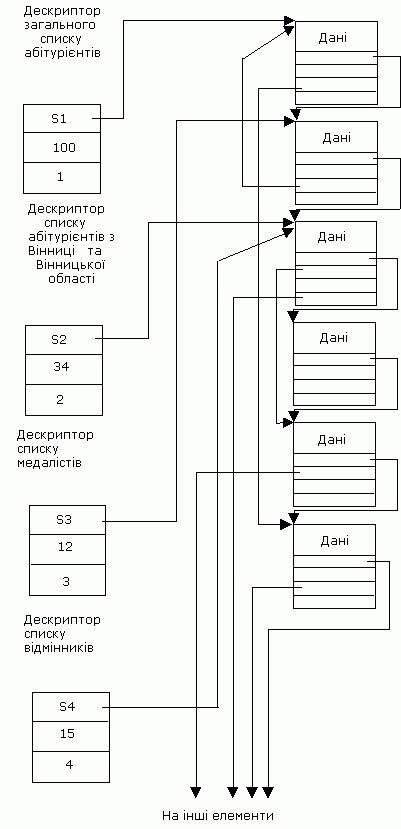
Рис. 5.8 Фрагмент чотиризв'язного списку
Метод лічильника зводиться до того, що після кожної операції виключення елементу з того чи іншого списку виконується перевірка, чи залишився даний елемент хоча б в якому-небудь одному функціональному списку.
згідно методу в кожному елементі багатозв'язної структури вводиться спеціальне поле. Вміст вказаного поля збільшується на одиницю при формуванні кожного зв'язку і зменшується на одиницю при кожному розриві зв'язку. Якщо значення додатково введеного поля включає нульове, то елемент може бути виключений, оскільки він не входить до складу жодного списку.
В методі "збору сміття" не вимагається при розриві кожного зв'язку , який направлений до елементу, виконувати перевірку на предмет виключення елементу із списку та переводити його у вільний список. Для цього кожному елементу даних відводять однорозрядне поле для маркера.
Елемент, який вивільняється як би "провисає" до тих пір, поки не буде вичерпано вільний список. Тільки після цього запускається процедура "збору сміття".
Суть методу полягає в тому, що сканується виділена ділянка пам'яті і обнуляються всі маркерні поля. Під час другого проходу всі маркери всіх елементів, які входять в списку , встановлюються в одиничний стан. При третьому скануванні виділеної ділянки пам'яті всі елементи, маркери яких мають нульове значення, вилучаються.