Теорія катастроф

П Л А Н

Введення

1. Історія

2. Сім елементарних катастроф по Тому

2.1 Потенційні функції з однієї активної змінної

2.1.1 Катастрофа типу "Складка"

2.1.2 Катастрофа типу "Збірка"

2.1.3 Катастрофа типу "ластівчин хвіст"

2.1.4 Катастрофа типу "Метелик"

2.2 Потенційні функції з двома активними змінними

2.2.1 Гіперболічна омбіліка

2.2.2 Еліптична омбіліка

2.2.3 Параболічна омбіліка

3. Запис і класифікація катастроф по Арнольду

4. Застосування теорії катастроф

5. Література

Введення

Теорія катастроф - розділ математики, що включає в себе теорію біфуркацій диференціальних рівнянь ( динамічних систем) і теорію особливостей гладких відображень.

Терміни "катастрофа" і "теорія катастроф" були введені Рене Томом (Ren Thom) і Крістофером Зіманов (Christopher Zeeman) наприкінці 1960-х - початку 1970-х років ("катастрофа" в даному контексті означає різка якісна зміна об'єкту при плавному кількісному зміну параметрів, від яких він залежить). Однією з головних задач теорії катастроф є отримання так званої нормальної форми досліджуваного об'єкта (диференціального рівняння або відображення) в околиці "точки катастрофи" і побудована на цій основі класифікація об'єктів.

Теорія катастроф знайшла численні застосування в різних областях прикладної математики, фізики, а також в економіці.

1. Історія

Перші фундаментальні результати в області динамічних систем, пов'язані з теорією катастроф, належать А. Пуанкаре (метод нормальних форм в теорії диференціальних рівнянь) і А. А. Андронову (біфуркації динамічних систем). Основи теорії особливостей гладких відображень були закладені насамперед у працях американського тополога Хасслера Уїтні (Hassler Whitney) в 1940-х - 1950-х рр.., яким передувала лема Морса про нормальну форму функції в околиці невиродженої критичної точки.

В кінці 1960 -х розвитком цього напряму зайнявся відомий французький математик і Філдсівську лауреат 1958 року Рене Том. Проте популярність ідеї Уїтні і Тома придбали завдяки декільком публікаціям К. Зімана в 1970 -х, який активно пропагував теорію катастроф, порівнюючи її значення з винаходом математичного аналізу і кажучи про "революцію в математиці". Бурхливий розвиток теорії катастроф в 1970-і - 1990-і роки пов'язано з діяльністю Дж. Боардмана, Є. Бріскорна, Дж. Брюса, Дж. Мазера, Б. Мальгранжа, Р. Тома, Т. Волл, К. Зімана і особливо В. І. Арнольда і його учнів (А. ​​Н. Варченко, В. А. Васильєв, А. Б. Гівенталь, В. В. Горюнов, С. М. Гусейн-Заде, А. А. Давидов, В. М . Закалюкін, В. Д. Сєдих та ін.)

2. Сім елементарних катастроф по Тому

Теорія катастроф аналізує критичні точки (репетиції) потенціальної функції, тобто точки, де не тільки перша похідна функції дорівнює нулю, але й рівні нулю і похідні більш високого порядку. Динаміка розвитку таких точок може бути вивчена за допомогою розкладання потенціальної функції в ряд Тейлора за малих змін вхідних параметрів.

Якщо точки росту не є випадковими, а структурно стабільними, то ці точки існують як центри організації для особливих геометричних структур з низьким рівнем виродженості, з критичними параметрами (високим рівнем катастрофічності) в оточуючих їх областях фазового простору. Якщо потенціальна функція залежить від трьох або меншого числа активних змінних, і п'яти або менше активних параметрів, то в цьому випадку існує всього сім описаних узагальнених структур геометрій біфуркацій, яким можна приписати стандартні форми розкладу в ряд Тейлора, в які можна розкласти критичні точки за допомогою дифеоморфізму (гладкої трансформації, інверсія якої є теж гладкою). Сьогодні ці сім фундаментальних типів відомі під іменами, які їм дав Рене Том.

Функції з однією змінною:

Катастрофа типу Складка V = x3 + ax

Катастрофа типу Збірка V = x4 + ax2 + bx

Катастрофа типу Хвіст ластівки V = x5 + ax3 + bx2 + cx

Катастрофа типу Метелик V = x6 + ax4 + bx3 + cx2 + dx

Потенціальні функції з двома змінними:

Гіперболічна омбіліка V = x3 + y3 + axy + bx + cy

Еліптична омбіліка V = x3 / 3 − xy2 + a(x2 + y2) + bx + cy

Параболічна омбіліка V = yx2 + y4 + ax2 + by2 + cx + dy

2.1. Потенційні функції з однієї активної змінної

2.1.1. Катастрофа типу "Складка"

Стабільна і нестабільна частини екстремуму, який зникає при біфуркації типу "складка"

V = x 3 + a x

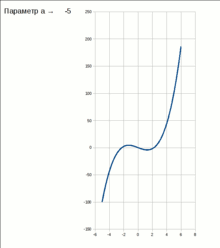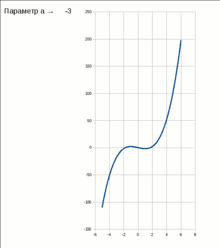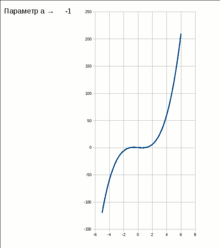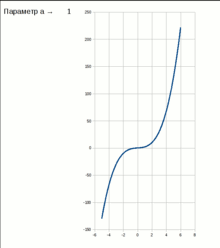При негативних значеннях параметра a, потенційна функція має два екстремуми - один стабільний (стійка рівновага) і один нестабільний (нестійка рівновага). Якщо параметр a повільно змінюється, система може перебувати в точці стабільного мінімуму. Але якщо a = 0, стабільні і нестабільний екстремуми зустрічаються і анігілюють. Це - точка біфуркації. При a> 0 не існує стабільного рішення.

Якщо фізична система проходить через точку біфуркації типу "згортка", і тому параметр a досягає значення 0, стабільність рішення при a <0 раптово втрачається, і система може здійснити раптовий перехід у новий, дуже відмінне від попереднього стан. Це біфуркаційні значення параметра a іноді називається "точкою фіксації".