НИУ МЭИ

Кафедра ФТЭМК

Реферат по курсу: Электрокерамические материалы и изделия

Тема: Магнитные свойства твердых тел

Группа: ЭЛ-14-08

Москва 2013.

1. ОБЩИЕ СВЕДЕНИЯ И ПАРАМЕТРЫ

МАГНИТНЫХ МАТЕРИАЛОВ

При помещении вещества в магнитное поле оно приобретает магнитный момент.

Для определение магнитных характеристик вещества вводятся специальные величины:

В, Тл (Тесла) –магнитная индукция

Н, А/м (Ампер на метр) – напряженность магнитного поля

М, А/м (Ампер на метр) – намагниченность

Ф, Вб (Вебер) – магнитный поток.

- магнитная восприимчивость

- магнитная проницаемость

В соответствии со своими магнитными свойствами все материалы можно разделить на следующие группы:

1)диамагнетики

2)парамагнетики

3)ферромагнетики

4)антиферромагнетики

5)ферримагнетики

По реакции на внешнее магнитное поле и характеру внутреннего магнитного упорядочения все вещества в природе можно подразделить на пять групп: диамагнетики, парамагнетики, ферромагнетики, антиферромагнетики и ферримагнетики. Перечисленным видам магнетиков соответствуют пять различных видов магнитного состояния вещества: диамагнетизм, парамагнетизм, ферромагнетизм, антиферромагнетизм и ферримагнетизм.

К диамагнетикам относят вещества, у которых магнитная восприимчивость отрицательна и не зависит от напряженности внешнего магнитного поля. К диамагнетикам относятся инертные газы, водород, азот, многие жидкости (вода, нефть и ее производные), ряд металлов (медь, серебро, золото, цинк, ртуть, галлий и др.), большинство полупроводников (кремний, германий, соединения А_ЗВ₅, А₂В₆) и органических соединений, щелочно-галоидные кристаллы, неорганические стекла и др. Диамагнетиками являются все вещества с ковалентной химической связью и вещества в сверхпроводящем состоянии.

К парамагнетикам относят вещества с положительной магнитной восприимчивостью, не зависящей от напряженности внешнего магнитного поля. К числу парамагнетиков относят кислород, окись азота, щелочные и щелочноземельные металлы, некоторые переходные металлы, соли железа, кобальта, никеля и редкоземельных элементов.В большинстве материалов внутренние силы выравнивания магнитной ориентации атомов отсутствуют, домены не образуются, и магнитные поля отдельных атомов направлены случайным образом. Из-за этого поля отдельных атомов-магнитов взаимно гасятся, и внешнего магнитного поля у таких материалов нет. Однако при помещении такого материала в сильное внешнее поле (например, между полюсами мощного магнита) магнитные поля атомов ориентируются в направлении, совпадающем с направлением внешнего магнитного поля, и мы наблюдаем эффект усиления магнитного поля в присутствии такого материла. Материалы, обладающие подобными свойствами, называются парамагнетиками. Стоит, однако убрать внешнее магнитное поле, как парамагнетик тут же размагничивается, поскольку атомы снова выстраиваются хаотично. То есть, парамагнетики характеризуются способностью к временному намагничиванию..

Некоторые вещества и сплавы (прежде всего, следует отметить железо, никель и кобальт) при температуре ниже точки Кюри приобретают свойство выстраивать свою кристаллическую решетку таким образом, что магнитные поля атомов оказываются однонаправленными и усиливают друг друга, благодаря чему возникает макроскопическое магнитное поле за пределами материла. Из таких материалов получаются постоянные магниты. На самом деле магнитное выравнивание атомов обычно не распространяется на неограниченный объем ферромагнитного материала: намагничивание ограничивается объемом, содержащим от нескольких тысяч до нескольких десятков тысяч атомов, и такой объем вещества принято называть доменом (от английского domain — «область»). При остывании железа ниже точки Кюри формируется множество доменов, в каждом из которых магнитное поле ориентировано по-своему. Поэтому в обычном состоянии твердое железо не намагничено, хотя внутри него образованы домены, каждый из которых представляет собой готовый мини-магнит. Однако под воздействием внешних условий (например, при застывании выплавленного железа в присутствии мощного магнитного поля) домены выстраиваются упорядоченно и их магнитные поля взаимно усиливаются. Тогда мы получаем настоящий магнит — тело, обладающее ярко выраженным внешним магнитным полем. Именно так устроены постоянные магниты.

К ферромагнетикам относят вещества с большой положительной магнитной восприимчивостью (до 10⁶), которая сильно зависит от напряженности магнитного поля и температуры.

Антиферромагнетиками являются вещества, в которых ниже некоторой температуры спонтанно возникает антипараллельная ориентация элементарных магнитных моментов одинаковых атомов или ионов кристаллической решетки. При нагревании антиферромагнетик испытывает фазовый переход в парамагнитное состояние. Антиферромагнетизм обнаружен у хрома, марганца и ряда редкоземельных элементов (Се, Nd, Sm, Тm и др.). Типичными антиферромагнетиками являются простейшие химические соединения на основе металлов переходной группы типа окислов, галогенидов, сульфидов, карбонатов и т.п.

К ферримагнетикам относят вещества, магнитные свойства которых обусловлены нескомпенсированным антиферромагнетизмом. Подобно ферромагнетикам они обладают высокой магнитной восприимчивостью, которая существенно зависит от напряженности магнитного поля и температуры. Наряду с этим ферримагнетики характеризуются и рядом существенных отличий от ферромагнитных материалов.

Свойствами ферримагнетиков обладают некоторые упорядоченные металлические сплавы, но, главным образом,- различные оксидные соединения, среди которых наибольший практический интерес представляют ферриты.

Орбитальный магнитный момент электрона

Источниками магнетизма являются магнитные моменты электронов и ядер атомов. Наибольший вклад в магнитный момент атома вносит электрон. Если предположить, что электрон вращается вокруг ядра атома (это предположения является не вполне точным с точки зрения квантовой механики), то можно выделить 2 вида момента электрона: спиновый и орбитальный. Орбитальный момент происходит из движения электрона по эллиптической орбите. Понятие спинового момента происходит из предположения, что электрон вращается вокруг собственной оси. Ниже подробнее описаны данные физические процессы.

Рассмотрим орбитальное движение электронов. Ограничиваясь классическим рассмотрением движения электрона по эллиптической орбите, можно представить, что оно эквивалентно электрическому току по замкнутой траектории, в результате чего возникает магнитный момент, величина которого определяется произведением силы тока на площадь орбиты:

.

(2.1)

Рис. 2.1. Эллиптическая орбита электрона

Если обозначить период вращения электрона через , то сила тока определяется по формуле

,

(2.2)

где е - заряд электрона.

Площадь электронной орбиты выражается через радиус-вектор и угол , который составляет радиус-вектор, проведенный из фокуса, с главным диаметром эллипса:

.

(2.3)

При движении электрона по орбите возникает момент количества движения электрона. По абсолютной величине момент P_l равен

,

(2.4)

где d/dt угловая скорость электрона по орбите; m - масса электрона.

Подставляя значения r² из (2.4) в (2.3), получаем

.

(2.5)

Затем, подставив в формулу (2.1) выражение для тока и площади орбиты, получаем величину орбитального магнитного момента электрона

.

(2.6)

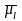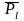Векторы и направлены в противоположные стороны в силу того, что заряд электрона отрицателен.

Из формулы следует, что отношение магнитного момента к механическому является величиной универсальной и не зависящей от радиуса. Это отношение получило название гиромагнитного орбитального отношения (иногда его называют магнитомеханическим)

.

(2.7)

Это отношение обычно выражется в единицах e/2m, тогда g_l=1. Рассмотренная модель атома является неустойчивой. Поэтому в 1913 году Бором была предложена полуквантовая модель строений атома, в соответствии с которой электроны занимают только дискретные орбиты, для которых механический момент является кратным постоянной Планка h (h=6,65х10³⁴ Дж_*с).

,

(2.8)

где l- угловые или орбитальные квантовые числа, которые могут принимать значение натурального ряда (n-1) в зависимости от главного квантового числа n.

l=0,1,2,3,…..(n-1).

Сопоставляя формулы (2.6) и (2.8) можно видеть, что квантуется и магнитный момент атома

,

(2.9)

где – магнетон Бора

Таким образом, в полуклассической квантовой теории механический момент электрона оказывался кратным постоянной Планка, а магнитный момент - магнетону Бора.

Квантовая механика внесла уточнения в такие представления. Было показано, что величина вектора механического момента в одноэлектронном атоме определяется по формуле:

.

(2.10)

Аналогично для магнитного момента

,

(2.11)

Так как и являются векторными величинами, то формально значение вектора приписывается величине .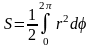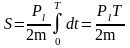