4. Понятие нормальной слау. Обоснование метода невязки

Пусть рассматривается система уравнений , тогда - невязка.

Комментарий. 1. Нелинейный оператор непрерывен в точке , если ; вполне непреры­вен, если он непрерывен и ограни­ченные множества отображает в предкомпакт­ные. В отличие от линейного случая непрерывность в точке не гарантирует непрерывности во всём простран­стве и не связана с ограниченностью.

Нелинейный оператор дифференцируем по Фреше в точке , если существует линейный огра­ниченный оператор (производная Фреше в точке или сильная производная), такой, что причём . Линейная часть приращения дифферен­циал Фреше.

Производная Фреше нелинейного опера­тора - это оператор , действую­щий как функция от х. В частном случае нелинейного функционала совокупность всех таких функ­ционалов, определённых на X, образует сопря­жённое пространство E*, поэтому производная Фреше функционала это вектор из E*: . Его назы­вают градиентом Фреше: .

Дифференциал Гато (слабый дифференциал) это предел по норме . Если этот предел линеен по , то есть , то оператор называется произ­водной Гато в точке .

Производная Фреше в точке совпадает с произ­водной Гато в точке . Производная Гато в точке сов­падает с производной Фреше в точке , если произ­водная Гато непрерывна по в этой точке.

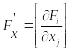2. Дифференцируемость всегда сводится к воз­можности линейной аппроксимации . В одномерном случае обычная производная, в случае перемен­ных градиент, а - скалярное произведение, для оператора матрица Якоби , а есть умножение мат­рицы на вектор. Скалярное произведение можно пред­ставить как функционал (функцию переменных в ко­нечномерном случае) и тогда дифференциал от неё тоже скалярное произведение. Напри­мер, в случае двумерного пространства . Тогда полный диффе­ренциал . После не­сложных преобразований получим . Дифференциал Фреше можно найти и сразу, как дифференциал от скалярного произведения: .

Введем понятие нормальной системы. Пусть . Тогда, приравнивая дифференциал Фреше к нулю, получим

. Тогда исходная система равносильна системе уравнений .

Определение. Система уравнений на­зывается нормальной, а переход от заданного СЛАУ к равносильной системе уравнений называется нормализацией СЛАУ.

Очевидно, что нормальная СЛАУ минимизирует невязку, так как

.

Таким образом, мини­мум невязки реализуется на решении нормаль­ного уравнения, метод наименьших квадратов просто один из вариантов метода невязки. Любое решение, минимизирующее невязку, называется псевдорешением. Если же оно получено нормали­зацией СЛАУ, оно называется нормальным псев­дорешением.

Культурный минимум

1. Что такое задача Чебышова? Постановка задачи.

2. Единственно ли наилучшее приближение в банаховом пространстве?

3. Какое множество называется выпуклым? Что такое строго выпуклое банахово пространство и как оно связано с единственностью наилучшего приближения?

4. Что такое псевдорешение (квазирешение) задачи ?

5. Что такое проецирование на заданные линейные оболочки?

6. Что такое метод наименьших квадратов?

7. Что такое дифференциал Фреше?

8. Какая СЛАУ называется нормальной и почему?

9. Что такое нормализация СЛАУ, псевдорешение, нормальное псевдорешение.