
- •VII. Проекционные методы. Псевдорешение
- •1. Проблема Бецалеля. Постановка задачи
- •2. Метод в.К.Иванова нахождения псевдорешений.
- •3. Несовместные системы. Метод матрицы Грама
- •3.1. Проецирование на заданные линейные оболочки
- •3.2. Метод наименьших квадратов
- •4. Понятие нормальной слау. Обоснование метода невязки
- •Культурный минимум
- •Вопросы по теме
VII. Проекционные методы. Псевдорешение
- Г-голубчики, сказал Федор Симеонович озадаченно... Это же проблема Бен Б-бецалеля. К-калиостро же доказал, что она н-не имеет р-решения. - Мы сами знаем, что она не имеет решения, сказал Хунта, немедленно ощетиниваясь. – Мы хотим знать, как ее решать. - К-как-то ты странно рассуждаешь, К-кристо... К-как же искать решение, к-когда его нет? Б-бессмыслица какая-то... - Извини, Теодор, но это ты очень странно рассуждаешь. Бессмыслица - искать решение, если оно и так есть. Речь идет о том, как поступать с задачей, которая решения не имеет. Это глубоко принципиальный вопрос... А. Стругацкий , Б. Стругацкий. Понедельник начинается в субботу
1. Проблема Бецалеля. Постановка задачи
Пусть

 банахово пространство, а
банахово пространство, а

 конечномерное подпространство, не
совпадающее с
.
При
использовании проекционных методов
исходная постановка задачи, как правило,
является компромиссом между, быть может,
противоречивыми требованиями. Такие
задачи или принципиально не имеют
решения, или решение не единственно. И
то и другое может сопровождаться
операторной неустойчивостью.
конечномерное подпространство, не
совпадающее с
.
При
использовании проекционных методов
исходная постановка задачи, как правило,
является компромиссом между, быть может,
противоречивыми требованиями. Такие
задачи или принципиально не имеют
решения, или решение не единственно. И
то и другое может сопровождаться
операторной неустойчивостью.
Определение.
Задачей
Чебышева
называют любую задачу о наилучшем
приближении элемента
 банахова
пространства
к
конечномерному подпространству
банахова
пространства
к
конечномерному подпространству
 .
Она ставится так:
.
Она ставится так:
 ,
надо указать элемент
,
надо указать элемент
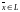 ,
такой, что
,
такой, что
 .
.
Комментарий.
Ясно, что
элемент будет приближать любой элемент
будет приближать любой элемент лучше, чем другие элементы из
.
Не ясно, существует ли такой элемент и
единственен ли он.
лучше, чем другие элементы из
.
Не ясно, существует ли такой элемент и
единственен ли он.
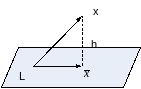
Теорема 1 (существование наилучшего приближения). Наилучшее приближение элемента банахова пространства к конечномерному подпространству существует.
 Пусть
банахово пространство, а
конечномерное подпространство, не
совпадающее с
.
Укажем элемент
Пусть
банахово пространство, а
конечномерное подпространство, не
совпадающее с
.
Укажем элемент
 ,
такой, что
,
такой, что
 .
Для этого введём в
некоторый базис
.
Для этого введём в
некоторый базис
 .
Тогда
.
Тогда
 .
Соответствующая эвклидова норма в
эвклидовом базисе
.
Соответствующая эвклидова норма в
эвклидовом базисе
 имеет вид
имеет вид
 .
В конечномерных пространствах все
нормы эквивалентны, то есть
.
В конечномерных пространствах все
нормы эквивалентны, то есть
 .
Рассмотрим функцию
.
Рассмотрим функцию
 ,
,
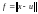 .
Она непрерывна, так как
.
Она непрерывна, так как
 ,
то есть если ,
то и
,
то есть если ,
то и
 .
Рассмотрим теперь шар
.
Рассмотрим теперь шар
 ,
где
,
где
 .
Вне шара
.
Вне шара
 .
Так как
.
Так как
 ,
и так как
,
и так как
 ,
а
,
а
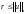 ,
то
,
то
 и неравенство только усилится, если
и неравенство только усилится, если
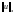 заменить на меньшее выражение
заменить на меньшее выражение
 .
Тогда
.
Тогда
 .
Таким образом, инфинум
.
Таким образом, инфинум
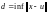 недостижим вне этого шара. Это означает,
что внутри шара, то есть замкнутого
ограниченного множества в конечномерном
пространстве, то есть компакта, функция
достигает инфинума (теорема Вейерштрасса).
недостижим вне этого шара. Это означает,
что внутри шара, то есть замкнутого
ограниченного множества в конечномерном
пространстве, то есть компакта, функция
достигает инфинума (теорема Вейерштрасса).
Комментарий.
Таким образом, наилучшее приближение
элемента х
пространства
к подпространству L
существует. Покажем, что оно не
единственно. Пусть пространство Х
есть плоскость
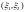 ,
а
,
а
 .
Введём на Х
норму
.
Введём на Х
норму
 .
Пусть
.
Пусть
 .
.

Тогда
 .
.

Из графика этой
функции видно, что при
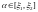 решение не единственно.
решение не единственно.
Определение.
Множество
 называется
выпуклым, если из того, что
называется
выпуклым, если из того, что
 ,
следует, что
принадлежит и весь отрезок, соединяющий
точки
,
следует, что
принадлежит и весь отрезок, соединяющий
точки
 ,
то есть совокупность всех точек х
вида
,
то есть совокупность всех точек х
вида
 .
.
Определение.
Банахово
пространство
называется
строго выпуклым, если
 для любого действительного скаляра
для любого действительного скаляра
 и любых
и любых
 .
.
Комментарий.
Пространства
 при
при
 строго выпуклы, а при
строго выпуклы, а при
 нет. Пространство
нет. Пространство
 не строго выпукло. Показано, что в нём
проекция единственна только на
подмножестве полиномов степени не
выше
не строго выпукло. Показано, что в нём
проекция единственна только на
подмножестве полиномов степени не
выше
 .
.
Теорема 2 (единственность наилучшего приближения).
Пусть
строго
выпуклое
банахово пространство, а
конечномерное подпространство, не
совпадающее с Х, причём
.
Тогда
 ,
такой, что
.
,
такой, что
.
![]() Существование
доказано в теореме 1. Осталось показать
единственность.
Существование
доказано в теореме 1. Осталось показать
единственность.
![]() .
Пусть
.
Пусть
![]()
![]() два наилучших приближения какого-то
х.
Тогда
два наилучших приближения какого-то
х.
Тогда![]() .
.
Так как
![]() строго выпуклое банахово пространство,
то
строго выпуклое банахово пространство,
то![]() ,
так как при
,
так как при
![]()
![]() .
Тогда
.
Тогда![]() ,
так как это линейная комбинация элементов
из
,
так как это линейная комбинация элементов
из
![]() .
Но по условию
.
Но по условию![]() .
Это противоречие и доказывает теорему.
.
Это противоречие и доказывает теорему.
Комментарий.
1. Как найти наилучшее приближение?
В банаховых пространствах общего способа
не существует. В гильбертовых пространствах
такой общий способ даёт задача
ортогонализации, приводящая к понятию
ряда Фурье. Пусть
![]() –
подпространство гильбертова пространства,
а
–
подпространство гильбертова пространства,
а
 подпространство, ортогональное к
.
Тогда гильбертово пространство
подпространство, ортогональное к
.
Тогда гильбертово пространство
![]() .
Так как
.
Так как
![]() – сепарабельное пространство, то в
нем всегда есть ортонормированная
система векторов:
– сепарабельное пространство, то в
нем всегда есть ортонормированная
система векторов:
![]() ,
где
,
где
![]() символ Кронекера. Проекция вектора
символ Кронекера. Проекция вектора
![]() на
вектор
на
вектор
![]() ,
где
,
где
![]() .
Мы будем искать те значения коэффициентов
разложения
.
Мы будем искать те значения коэффициентов
разложения
![]() ,
при которых невязка (квадрат невязки)
,
при которых невязка (квадрат невязки)
![]() будет минимальна:
будет минимальна:
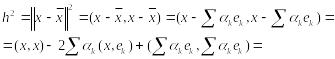
 .
.
Ясно,
что это выражение будет принимать
минимальное значение при
![]() и
и
![]() .
Тогда
.
Тогда
![]() .
Отсюда получаем неравенство Бесселя
.
Отсюда получаем неравенство Бесселя
![]() .
При
.
При
![]() ортонормированная система векторов
(ОНС) называется полной ортонормированной
системой в смысле Стеклова (ПОНС). Отсюда
можно получить равенство Стеклова
–Парсеваля
ортонормированная система векторов
(ОНС) называется полной ортонормированной
системой в смысле Стеклова (ПОНС). Отсюда
можно получить равенство Стеклова
–Парсеваля
 теорему
Пифагора для гильбертовых пространств.
теорему
Пифагора для гильбертовых пространств.
2. Пусть
![]() ,
где
,
где
 компактный оператор. Если
компактный оператор. Если
![]() ,
где
компакт, то в соответствии с теоремой
Тихонова такая задача условно устойчива.
Рассмотрим случай, когда
,
где
компакт, то в соответствии с теоремой
Тихонова такая задача условно устойчива.
Рассмотрим случай, когда
![]() .
.
Задача Чебышёва в применении к решению операторных уравнений I рода приводит к понятию псевдорешения (квазирешения) и методу В.К.Иванова нахождения псевдорешений.
