Пример. Рассмотрим оператор ,действующий по формуле .Показать, что оператор а непрерывно обратим. Найти .
Линейный оператор
называется непрерывно обратимым, если
и существует обратный ограниченный
оператор.
Рассмотрим
уравнение вида
и покажем, что для
существует единственное решение
уравнения. Это будет означать, что для
оператора А
существует
.
Полученное
уравнение эквивалентно интегральному
уравнению. Если данное уравнение имеет
единственное решение, то исходное также
будет однозначно разрешимым. Вычислим
с:
,
тогда
.
Это означает разрешимость уравнения при . Следовательно,
.
Заметим, что это
интегральный оператор с непрерывным
ядром, который является ограниченным.
Таким образом, к оператору А
существует
ограниченный обратный и
,
поэтому
оператор А
непрерывно обратим.
Пример.
Рассмотрим оператор
,
с областью определения
.
Доказать , что А
– неограниченный линейный оператор.
Доказать , что А
– непрерывно обратим, найти
.
Оператор А
неограничен, так как последовательность
с
под действием оператора перейдет в
последовательность
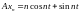и
при
.
Рассмотрим на
уравнение
и
решим его методом Эйлера:
.
Значит,
,
,
ограничен, т.е.
.
Действительно,
.
Следовательно, А неограниченный непрерывно обратимый оператор.
Пример.
Рассмотрим оператор
,
действующий по формуле
.
Доказать , что А
непрерывно обратим , найти
.
Оператор А
является интегральным оператором
Вольтера с непрерывным ядром, поэтому
А
ограничен. Рассмотрим уравнение
.
,
где
,
причем
и
Следовательно, решение интегрального уравнения Вольтера равносильно решению следующей задачи Коши для ОДУ:
Выпишем решение задачи Коши по методу Лагранжа:
.
Значит
.
Это оператор Вольтера 2-го рода и поэтому
он ограничен.
Культурный минимум
Какой линейный оператор называется обратимым? Что такое обратный оператор?
Что такое ядро, образ, область определения, множество значений линейного оператора?
Какой оператор называется непрерывно обратимым?
Что такое операторная устойчивость уравнения
Какая задача корректно разрешима по Адамару?
Какой оператор называется замкнутым? Почему и когда НЛО есть ЗЛО?
Что такое график оператора? Когда он замкнут?
Что такое корректность по Фикера? Что такое обобщённая разрешимость, нормальная разрешимость?
Что такое компактность метрических пространств? Что такое компактный оператор?
Вопросы
Доказать теорему о линейности обратного оператора.
Доказать критерий существования обратного оператора в конечномерном случае. Привести контрпример для бескономерного случая.
Доказать критерий непрерывности обратного оператора.
Доказать теорему Банаха о гомеоморфизме.
Доказать теорему о замкнутости линейного оператора и теорему Банаха о замкнутом графике.
Доказать критерий замкнутости линейного оператора.
Доказать критерий Фикера разрешимости уравнения
Доказать, что компактный оператор всегда ограничен.
Доказать, что если – компактный оператор, – ограниченный в банаховом пространстве , то операторы и – компактны.
Доказать, что оператор Фредгольма непрерывен в пространствах и .
Доказать, что оператор Фредгольма компактен в пространствах и .
Доказать, что интегральный оператор Фредгольма не имеет ограниченного обратного.
Доказать, что компактный оператор имеет замкнутое множество значений тогда и только тогда, когда конечномерно.
ЗАДАЧИ
Показать, что оператор дифференцирования не ограничен, если действует из в и ограничен на паре пространств .
Показать, что на паре пространств прямая задача дифференцирования корректна, обратная - не корректна.
Показать, что единичный оператор не компактен.
Показать, что оператор незамыкаем как фунционал на непрерывно дифференцируемых функциях на
.Является ли компактным оператор
,
если
.Показать, что оператор дифференцирования не компактен при действии и компактен при действии .
Показать, что оператор , непрерывно обратим. Найти .
Доказать, что оператор , с областью определения неограниченный непрерывно обратимый оператор. Найти .
Доказать, что оператор , действующий по формуле непрерывно обратим , найти .