3. Корректность компактных операторов

Определение. Линейный оператор , отображающий банахово пространство в себя (или другое банахово пространство), называется компактным (вполне непрерывным), если каждое ограниченное множество он переводит в предкомпактное.

Комментарий. Напомним, что множество метрического пространства компактно, если из любого бесконечного его подмножества можно выделить последовательность, сходящуюся к элементу из , и предкомпактно, если замыкание компактно. Если линейный оператор компактен, то он переводит любую ограниченную последовательность в компактную последовательность , то есть из любой подпоследовательности последовательности можно выделить сходящуюся подпоследовательность. Компактность и предкомпактность это, прежде всего, свойства пространств. Суть компактности в исчерпываемости некого бесконечномерного пространства конечномерным приближением с любой наперед заданной точностью. Компактный оператор наследует свойства конечномерного оператора в том смысле, что всегда может быть приближен им.

Теорема1. Компактный оператор всегда ограничен.

. Пусть компактный оператор не ограничен. Тогда найдется последовательность , такая, что . Но тогда из неё нельзя выделить сходящуюся подпоследовательность, что противоречит тому, что вполне непрерывный оператор.

Комментарий. Не любой непрерывный линейный оператор вполне непрерывен. Рассмотрим, например, единичный оператор . Он, очевидно, ограничен, но не компактен. Покажем это.

В пространстве существует бесконечная ортонормированная система (ОНС) , такая, что . Ясно, что последовательность лежит на сфере , то есть она ограничена, но из неё нельзя выделить сходящуюся подпоследовательность, так как . То есть единичная сфера в гильбертовом пространстве– замкнутое и ограниченное множество, но не компакт, а . Таким образом, единичный оператор не компактен.

Можно показать, что единичный оператор в любом бесконечномерном банаховом пространстве не компактен. Это следует из теоремы Рисса о некомпактности единичного шара в бесконечномерном - пространстве.

Пример. Является ли вполне непрерывным оператор , если .

Оператор А задан не на всем пространстве . Действительно, если рассмотреть функцию , то и интеграл является расходящимся. Оператор А поэтому не является ограниченным и, следовательно, вполне непрерывным как отображение из в .

Теорема2. Если – компактный оператор, – ограниченный в банаховом пространстве , то операторы и – компактны.

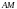Если множество ограничено, то множество тоже ограничено. Следовательно, множество предкомпактно, а это и означает, что оператор компактен. Далее, если ограничено, то предкомпактно, а тогда в силу непрерывности множество тоже предкомпактно, то есть оператор компактен.

В качестве основного примера линейного оператора рассмотрим оператор Фредгольма в пространстве , сопоставляющий функции новую функцию , определенную с помощью формулы , где некоторая непрерывная функция двух переменных. Оператор A называется интегральным, его линейность очевидна из линейности интеграла. Если ядро непрерывно по совокупности аргументов, то в соответствии с теоремой о непрерывной зависимости от параметра собственного интеграла, оператор A действует в линейном функциональном пространстве.

Теорема 3. Оператор Фредгольма непрерывен в пространствах и .

1. Покажем, что оператор Фредгольма непрерывен в пространстве

Таким образом, . Но непрерывная и, следовательно, ограниченная на сегменте функция, то есть и .

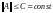2. Покажем, что оператор Фредгольма ограничен и, следовательно, непрерывен в пространстве . По неравенству Коши Буняковского для каждого фиксированного , полагая, что , можно записать = . Интегрируем по : . Правая часть неравенства не зависит от и ограниченна, поэтому .

Теорема 4. Пусть функция непрерывна на квадрате 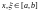. Тогда интегральный оператор Фредгольма компактен в пространствах и .

Докажем сначала компактность интегрального оператора Фредгольма в пространстве . Рассмотрим последовательность и последовательность .

1. Покажем равностепенную непрерывность последовательности . На квадрате функция равномерно непрерывна по теореме Кантора, так как она непрерывна на замкнутом и ограниченном множестве в . Значит, Оценим разность: при :

.

То есть последовательность равностепенно непрерывна.

2. Покажем равномерную ограниченность последовательности . Пусть . Тогда , а это и есть равномерная ограниченность. Итак, множество функций равномерно ограничено и равностепенно непрерывно, то есть в соответствии с критерием Арцела оператор является вполне непрерывным в пространстве . Но, так как из равномерной сходимости следует сходимость в среднем, оператор является вполне непрерывным и при действии из в .

Теорема5. Интегральный оператор Фредгольма не имеет ограниченного обратного.

Рассмотрим единичный шар в гильбертовом пространстве. Шар – замкнутое и ограниченное множество, но не компакт. Подействуем на него оператором . Если компактный оператор, то компакт. Если ограничен, то шар компакт или предкомпакт, что противоречит некомпактности единичного шара.

Комментарий. Итак, задача может оказаться корректной в одной паре пространств и некорректной в другой. Но некорректность интегрального уравнения Фредгольма первого рода не зависит от выбора пространств и устанавливается от противного: если задача корректна, то существует непрерывный оператор , и, следовательно, тождественный оператор компактен в соответствующем бесконечномерном пространстве, что невозможно.

Теорема 6. Вполне непрерывный оператор имеет замкнутое множество значений тогда и только тогда, когда конечномерно.

. Пусть вполне непрерывный оператор, замкнуто и бесконечномерно. Тогда в силу теоремы 4 из пункта 2 существует ограниченный обратный оператор , определенный на всем , и поэтому произведение будет также вполне непрерывным оператором. Это противоречит теореме Рисса о некомпактности единичного шара в бесконечномерном пространстве. Обратное утверждение очевидно.

Пример. Покажем, что оператор дифференцирования не компактен при действии и компактен при действии .

1. Рассмотрим в пространстве последовательность . Эта последовательность ограничена в , так как . Однако последовательность образов ее элементов некомпактна в пространстве . Чтобы это показать, рассмотрим . Выберем . Тогда при видно, что , то есть ни сама последовательность, ни любая её подпоследовательность даже не фундаментальны. Поэтому оператор дифференцирования не является компактным при действии .

2. Рассмотрим случай . Пусть - произвольная ограниченная последовательность в пространстве , то есть . Ясно, что и . Последовательность состоит из равномерно ограниченных непрерывных функций. Более того, последовательность равностепенно непрерывна. Действительно, так как , то найдётся такое , что . Поэтому

. Это и означает, что последовательность не только равномерно ограниченна, но и равностепенно непрерывна, то есть компактна по критерию Арцела.

Комментарий. Таким образом, на паре пространств прямая задача дифференцирования корректна, обратная не корректна, так как оператор становится компактным и поэтому не имеет ограниченного обратного.